histcounts2

Количество интервалов двумерной гистограммы

Синтаксис

[N,Xedges,Yedges]
= histcounts2(X,Y)

[N,Xedges,Yedges]
= histcounts2(X,Y,nbins)

[N,Xedges,Yedges]
= histcounts2(X,Y,Xedges,Yedges)

[N,Xedges,Yedges]
= histcounts2(___,Name,Value)

[N,Xedges,Yedges,binX,binY]
= histcounts2(___)

Описание

пример

[N,Xedges,Yedges] = histcounts2(X,Y) делит значения в X и Y в 2D интервалы, и возвращает количество интервалов, а также границы интервала в каждой размерности. histcounts2 функционируйте использует автоматический алгоритм раскладывания, который возвращает универсальные интервалы, выбранные, чтобы покрыть область значений значений в X и Y и покажите базовую форму распределения.

пример

[N,Xedges,Yedges] = histcounts2(X,Y,nbins) задает количество интервалов, чтобы использовать в каждой размерности.

пример

[N,Xedges,Yedges] = histcounts2(X,Y,Xedges,Yedges) разделы X и Y в интервалы с границами интервала, заданными Xedges и Yedges.

N(i,j) считает значение [X(k),Y(k)] если Xedges(i) ≤ X(k) <Xedges(i+1) и Yedges(j) ≤ Y(k) <Yedges(j+1). Последние интервалы в каждой размерности также включают последнее (внешнее) ребро. Например, [X(k),Y(k)] попадает в iинтервал th в последней строке, если Xedges(end-1) ≤ X(k) ≤ Xedges(end) и Yedges(i) ≤ Y(k) <Yedges(i+1).

пример

[N,Xedges,Yedges] = histcounts2(___,Name,Value) дополнительные опции использования заданы одним или несколькими Name,Value парные аргументы с помощью любого из входных параметров в предыдущих синтаксисах. Например, можно задать 'BinWidth' и двухэлементный вектор, чтобы настроить ширину интервалов в каждой размерности.

пример

[N,Xedges,Yedges,binX,binY] = histcounts2(___) также возвращает массивы индекса binX и binY, использование любого из предыдущих синтаксисов. binX и binY массивы одного размера с X и Y чьими элементами являются индексы интервала для соответствующих элементов в X и Y. Число элементов в (i,j)интервал th равен nnz(binX==i & binY==j), который совпадает с N(i,j) если Normalization 'count'.

Примеры

свернуть все

Количества интервала и края интервала

Скрипт Open Live Script

Распределите 100 пар случайных чисел в интервалы. histcounts2 автоматически выбирает соответствующую ширину интервала, чтобы показать базовое распределение данных.

x = randn(100,1);
y = randn(100,1);
[N,Xedges,Yedges] = histcounts2(x,y)

N = 7×6

     0     0     0     2     0     0
     1     2    10     4     0     0
     1     4     9     9     5     0
     1     4    10    11     5     1
     1     4     6     3     1     1
     0     0     1     2     0     0
     0     0     1     0     1     0

Xedges = 1×8

    -3    -2    -1     0     1     2     3     4

Yedges = 1×7

    -3    -2    -1     0     1     2     3

Определение количества интервалов в каждой размерности

Скрипт Open Live Script

Распределите 10 пар чисел в 12 интервалов. Задайте 3 интервала в x-размерности и 4 интервала в y-размерности.

x = [1 1 2 3 2 2 1 1 2 3];
y = [5 6 3 8 9 1 2 7 5 1];
nbins = [3 4];
[N,Xedges,Yedges] = histcounts2(x,y,nbins)

N = 3×4

     1     0     2     1
     1     1     1     1
     1     0     0     1

Xedges = 1×4

    0.6000    1.4000    2.2000    3.0000

Yedges = 1×5

         0    2.3000    4.6000    6.9000    9.2000

Определение краев интервала

Скрипт Open Live Script

Распределите 1 000 пар случайных чисел в интервалы. Задайте границы интервала с двумя векторами: один каждый для размерностей X и Y. Первый элемент в каждом векторе задает первое ребро первого интервала, и последним элементом является последнее ребро последнего интервала.

x = randn(1000,1);
y = randn(1000,1);
Xedges = -5:5;
Yedges = [-5 -4 -2 -1 -0.5 0 0.5 1 2 4 5];
N = histcounts2(x,y,Xedges,Yedges)

N = 10×10

     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     1     1     1     0     0     0
     0     0     5     5     3     5     1     2     0     0
     0     2    19    23    29    25    26    20     5     0
     0    10    36    51    59    71    54    46    10     0
     0     7    43    46    79    64    60    46     9     0
     0     3    12    18    21    23    19     9     6     0
     0     0     5     3     2     8     2     2     0     0
     0     0     0     1     1     1     0     0     0     0
     0     0     0     0     0     0     0     0     0     0

Нормализованные количества интервала

Скрипт Open Live Script

Распределите 1 000 пар случайных чисел в интервалы. Задайте Normalization как 'probability' нормировать количество интервалов, таким образом что sum(N(:)) 1. Таким образом, каждое количество интервала представляет вероятность, что наблюдение находится в пределах того интервала.

x = randn(1000,1);
y = randn(1000,1);
[N,Xedges,Yedges] = histcounts2(x,y,6,'Normalization','probability')

N = 6×6

         0         0    0.0020    0.0020         0         0
         0    0.0110    0.0320    0.0260    0.0070    0.0010
    0.0010    0.0260    0.1410    0.1750    0.0430    0.0060
         0    0.0360    0.1620    0.1940    0.0370    0.0040
         0    0.0040    0.0300    0.0370    0.0100    0.0010
         0    0.0030    0.0040    0.0040    0.0010         0

Xedges = 1×7

   -4.0000   -2.7000   -1.4000   -0.1000    1.2000    2.5000    3.8000

Yedges = 1×7

   -4.0000   -2.7000   -1.4000   -0.1000    1.2000    2.5000    3.8000

Определение размещения интервала

Скрипт Open Live Script

Распределите 1 000 случайных целочисленных пар между-10 и 10 в интервалы и задайте BinMethod как 'integers' использовать интервалы модульной ширины, сосредоточенные на целых числах. Задайте пять выходных параметров для histcounts2 возвратить векторы, представляющие размещение интервала данных.

x = randi([-10,10],1000,1);
y = randi([-10,10],1000,1);
[N,Xedges,Yedges,binX,binY] = histcounts2(x,y,'BinMethod','integers');

Определите который интервал значение (x(3),y(3)) падения в.

[x(3),y(3)]

ans = 1×2

    -8    10

bin = [binX(3) binY(3)]

bin = 1×2

     3    21

Входные параметры

свернуть все

`X,Y` — Данные, чтобы распределить среди интервалов (в качестве отдельных аргументов)
векторы | матрицы | многомерные массивы

Данные, чтобы распределить среди интервалов в виде отдельных аргументов векторов, матриц или многомерных массивов. X и Y должен иметь тот же размер.

Соответствующие элементы в X и Y задайте x и координаты y точек 2D данных, [X(k),Y(k)]. Типы данных X и Y может отличаться.

histcounts2 игнорирует весь NaN значения. Точно так же histcounts2 игнорирует Inf и -Inf значения, если границы интервала явным образом не задают Inf или -Inf как граница интервала.

`nbins` — Количество интервалов в каждой размерности
скаляр | вектор

Количество интервалов в каждой размерности в виде положительного скалярного целого числа или двухэлементного вектора из положительных целых чисел. Если вы не задаете nbins, затем histcounts2 автоматически вычисляет сколько интервалов, чтобы использовать на основе значений в X и Y:

Если nbins скаляр, затем histcounts2 использование, что много интервалов в каждой размерности.
Если nbins вектор, затем nbins(1) задает количество интервалов в x - размерность и nbins(2) задает количество интервалов в y - размерность.

Пример: [N,Xedges,Yedges] = histcounts2(X,Y,[15 20]) использование 15 интервалов в x- размерность и 20 интервалов в y- размерность.

`Xedges` — Границы интервала в x - размерность
вектор

Границы интервала в x - размерность в виде вектора. Xedges(1) первое ребро первого интервала в x - размерность и Xedges(end) внешний край последнего интервала.

`Yedges` — Границы интервала в y - размерность
вектор

Границы интервала в y - размерность в виде вектора. Yedges(1) первое ребро первого интервала в y - размерность и Yedges(end) внешний край последнего интервала.

Аргументы name-value

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: [N,Xedges,Yedges] = histcounts2(X,Y,'Normalization','probability') нормирует количество интервалов в N, таким образом, что sum(N) 1.

`BinMethod` — Алгоритм раскладывания
`'auto'` (значение по умолчанию) | `'scott'` | `'fd'` | `'integers'`

Алгоритм раскладывания в виде одного из значений в этой таблице.

Значение	Описание
`'auto'`	`'auto'` по умолчанию алгоритм выбирает, ширина интервала, чтобы покрыть данные располагаются и показывают форму базового распределения.
`'scott'`	Правило Скотта оптимально, если данные близко к тому, чтобы быть совместно нормально распределенным. Это правило подходит для большинства других распределений, также. Это использует размер интервала `[3.5std(X(:))numel(X)^(-1/4), 3.5std(Y(:))numel(Y)^(-1/4)]`.
`'fd'`	Правило Фридмена—Диакониса менее чувствительно к выбросам в данных и может более подойти для данных с распределениями с тяжелым хвостом. Это использует размер интервала `[2IQR(X(:))numel(X)^(-1/4), 2IQR(Y(:))numel(Y)^(-1/4)]`, где `IQR` межквартильный размах.
`'integers'`	Целочисленное правило полезно с целочисленными данными, когда это создает интервалы, сосредоточенные на парах целых чисел. Это использует ширину интервала 1 для каждой размерности и помещает границы интервала на полпути между целыми числами. Чтобы постараться не случайно создавать слишком много интервалов, можно использовать это правило, чтобы создать предел 1 024 интервалов (2¹⁰). Если область значений данных для любой размерности больше 1024, то целочисленное правило использует более широкие интервалы вместо этого.

histcounts2 не всегда выбирает количество интервалов с помощью этих точных формул. Иногда количество интервалов настроено немного так, чтобы границы интервала упали на "хорошие" числа.

Пример: [N,Xedges,Yedges] = histcounts2(X,Y,'BinMethod','integers') использует 2D интервалы, сосредоточенные на каждой паре целых чисел.

`BinWidth` — Ширина интервалов в каждой размерности
вектор

Ширина интервалов в каждой размерности в виде двухэлементного вектора из положительных целых чисел, [xWidth yWidth].

Если вы задаете BinWidthто histcounts2 может использовать максимум 1 024 интервалов (2¹⁰) по каждому измерению. Если заданная ширина интервала требует большего количества интервалов, то histcounts2 использует большую ширину интервала, соответствующую максимальному количеству интервалов.

Пример: [N,Xedges,Yedges] = histcounts2(X,Y,'BinWidth',[5 10]) интервалы использования с размером 5 в x- размерность и размер 10 в y- размерность.

`XBinLimits` — Интервал ограничивает в x - размерность
двухэлементный вектор

Интервал ограничивает в x - размерность в виде двухэлементного вектора, [xbmin,xbmax]. Вектор указывает на первые и последние границы интервала в x - размерность.

Эта опция только данные об интервалах, которые находятся в пределах пределов интервала включительно, X>=xbmin & X<=xbmax.

`YBinLimits` — Интервал ограничивает в y - размерность
двухэлементный вектор

Интервал ограничивает в y - размерность в виде двухэлементного вектора, [ybmin,ybmax]. Вектор указывает на первые и последние границы интервала в y - размерность.

Эта опция только данные об интервалах, которые находятся в пределах пределов интервала включительно, Y>=ybmin & Y<=ybmax.

`Normalization` — Тип нормализации
`'count'` (значение по умолчанию) | `'probability'` | `'countdensity'` | `'pdf'` | `'cumcount'` | `'cdf'`

Тип нормализации в виде одного из значений в этой таблице. Для каждого интервала i:

$v_{i}$ значение интервала.
$c_{i}$ число элементов в интервале.
$A_{i} = w_{x i} \cdot w_{y i}$ область каждого интервала, вычисленное использование x и ширин интервала y.
$N$ число элементов во входных данных. Это значение может быть больше сгруппированных данных, если данные содержат NaN значения, или если некоторые данные находятся вне пределов интервала.

Значение	Значения интервала	Примечания
`'count'` (значение по умолчанию)	$v_{i} = c_{i}$	Количество или частота наблюдений. Сумма значений интервала меньше чем или равна `numel(X)` и `numel(y)`. Сумма меньше `numel(X)` только, когда некоторые входные данные не включены в интервалы.
`'countdensity'`	$v_{i} = \frac{c_{i}}{A_{i}}$	Количество или частота, масштабируемая областью интервала. Сумма объемов интервала, (N значение * область интервала), меньше чем или равна `numel(X)` и `numel(Y)`.
`'cumcount'`	$v_{i} = \sum_{j = 1}^{i} c_{j}$	Совокупное количество. Каждое значение интервала является совокупным числом наблюдений в каждом интервале и всех предыдущих интервалах и в x и в размерностях y. `N(end,end)` меньше чем или равно `numel(X)` и `numel(Y)`.
`'probability'`	$v_{i} = \frac{c_{i}}{N}$	Относительная вероятность. `sum(N(:))` меньше чем или равно `1`.
`'pdf'`	$v_{i} = \frac{c_{i}}{N \cdot A_{i}}$	Оценка функции плотности вероятности. Сумма объемов интервала, (N значение * область интервала), меньше чем или равна `1`.
`'cdf'`	$v_{i} = \sum_{j = 1}^{i} \frac{c_{j}}{N}$	Совокупная оценка функции плотности. `N(end,end)` меньше чем или равно `1`.

Пример: [N,Xedges,Yedges] = histcounts2(X,Y,'Normalization','pdf') интервалы данные с помощью функции плотности вероятности оценивают для X и Y.

Выходные аргументы

свернуть все

`N` bincounts
массив

Количество интервалов, возвращенное как числовой массив.

Схема включения интервала различных пронумерованных интервалов в N, а также их относительная ориентация к x - оси и y - ось,

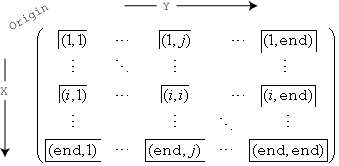
Например, (1,1) интервал включает значения, которые падают на первое ребро в каждой размерности, и последний интервал в правом нижнем включает значения, которые падают на любое из его ребер.

`Xedges` — Границы интервала в x - размерность
вектор

Границы интервала в x - размерность, возвращенная как вектор. Xedges(1) первая граница интервала в x - размерность и Xedges(end) последняя граница интервала.

`Yedges` — Границы интервала в y - размерность
вектор

Границы интервала в y - размерность, возвращенная как вектор. Yedges(1) первая граница интервала в y - размерность и Yedges(end) последняя граница интервала.

`binX` — Индекс интервала в x - размерность
массив

Индекс интервала в x - размерность, возвращенная как числовой массив одного размера с X. Соответствующие элементы в binX и binY опишите, который пронумеровал интервал, содержит соответствующие значения в X и Y. Значение 0 в binX или binY указывает на элемент, который не принадлежит ни одному из интервалов (таких как NaN значение.

Например, binX(1) и binY(1) опишите размещение интервала для значения [X(1),Y(1)].

`binY` — Индекс интервала в y - размерность
массив

Индекс интервала в y - размерность, возвращенная как числовой массив одного размера с Y. Соответствующие элементы в binX и binY опишите, который пронумеровал интервал, содержит соответствующие значения в X и Y. Значение 0 в binX или binY указывает на элемент, который не принадлежит ни одному из интервалов (таких как NaN значение.

Например, binX(1) и binY(1) опишите размещение интервала для значения [X(1),Y(1)].

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Указания и ограничения по применению:

Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.
Если вы не предоставляете границы интервала, то генерация кода может потребовать массивов переменного размера и динамического выделения памяти.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.

Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.

Введенный в R2015b

Документация

histcounts2

Синтаксис

Описание

Примеры

Количества интервала и края интервала

Определение количества интервалов в каждой размерности

Определение краев интервала

Нормализованные количества интервала

Определение размещения интервала

Входные параметры

`X,Y` — Данные, чтобы распределить среди интервалов (в качестве отдельных аргументов)
векторы | матрицы | многомерные массивы

`nbins` — Количество интервалов в каждой размерности
скаляр | вектор

`Xedges` — Границы интервала в x - размерность
вектор

`Yedges` — Границы интервала в y - размерность
вектор

Аргументы name-value

`BinMethod` — Алгоритм раскладывания
`'auto'` (значение по умолчанию) | `'scott'` | `'fd'` | `'integers'`

`BinWidth` — Ширина интервалов в каждой размерности
вектор

`XBinLimits` — Интервал ограничивает в x - размерность
двухэлементный вектор

`YBinLimits` — Интервал ограничивает в y - размерность
двухэлементный вектор

`Normalization` — Тип нормализации
`'count'` (значение по умолчанию) | `'probability'` | `'countdensity'` | `'pdf'` | `'cumcount'` | `'cdf'`

Выходные аргументы

`N` bincounts
массив

`Xedges` — Границы интервала в x - размерность
вектор

`Yedges` — Границы интервала в y - размерность
вектор

`binX` — Индекс интервала в x - размерность
массив

`binY` — Индекс интервала в y - размерность
массив

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.

Смотрите также

Документация MATLAB

Поддержка

Документация

histcounts2

Синтаксис

Описание

Примеры

Количества интервала и края интервала

Определение количества интервалов в каждой размерности

Определение краев интервала

Нормализованные количества интервала

Определение размещения интервала

Входные параметры

X,Y — Данные, чтобы распределить среди интервалов (в качестве отдельных аргументов) векторы | матрицы | многомерные массивы

nbins — Количество интервалов в каждой размерности скаляр | вектор

Xedges — Границы интервала в x - размерность вектор

Yedges — Границы интервала в y - размерность вектор

Аргументы name-value

BinMethod — Алгоритм раскладывания 'auto' (значение по умолчанию) | 'scott' | 'fd' | 'integers'

BinWidth — Ширина интервалов в каждой размерности вектор

XBinLimits — Интервал ограничивает в x - размерность двухэлементный вектор

YBinLimits — Интервал ограничивает в y - размерность двухэлементный вектор

Normalization — Тип нормализации 'count' (значение по умолчанию) | 'probability' | 'countdensity' | 'pdf' | 'cumcount' | 'cdf'

Выходные аргументы

N bincounts массив

Xedges — Границы интервала в x - размерность вектор

Yedges — Границы интервала в y - размерность вектор

binX — Индекс интервала в x - размерность массив

binY — Индекс интервала в y - размерность массив

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью MATLAB® Coder™.

Основанная на потоке среда Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.

Смотрите также

Документация MATLAB

Поддержка

`X,Y` — Данные, чтобы распределить среди интервалов (в качестве отдельных аргументов)
векторы | матрицы | многомерные массивы

`nbins` — Количество интервалов в каждой размерности
скаляр | вектор

`Xedges` — Границы интервала в x - размерность
вектор

`Yedges` — Границы интервала в y - размерность
вектор

`BinMethod` — Алгоритм раскладывания
`'auto'` (значение по умолчанию) | `'scott'` | `'fd'` | `'integers'`

`BinWidth` — Ширина интервалов в каждой размерности
вектор

`XBinLimits` — Интервал ограничивает в x - размерность
двухэлементный вектор

`YBinLimits` — Интервал ограничивает в y - размерность
двухэлементный вектор

`Normalization` — Тип нормализации
`'count'` (значение по умолчанию) | `'probability'` | `'countdensity'` | `'pdf'` | `'cumcount'` | `'cdf'`

`N` bincounts
массив

`Xedges` — Границы интервала в x - размерность
вектор

`Yedges` — Границы интервала в y - размерность
вектор

`binX` — Индекс интервала в x - размерность
массив

`binY` — Индекс интервала в y - размерность
массив

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® `backgroundPool` или ускорьте код с Parallel Computing Toolbox™ `ThreadPool`.