PMLSM

Линейный синхронный двигатель с постоянными магнитами с синусоидальным распределением потока

Библиотека:
Simscape / Электрический / Электромеханический / Постоянный магнит

Описание

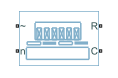
Блок PMLSM моделирует постоянный магнит линейный синхронный двигатель с трехфазным статором раны Уая. Рисунок показывает эквивалентную электрическую схему для обмоток статора.

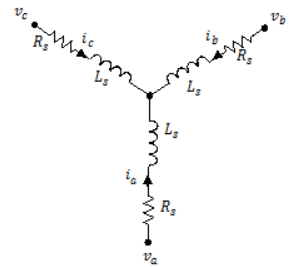
Можно также смоделировать постоянный магнит линейный синхронный двигатель в настройке раны дельты установкой Winding type к Delta-wound.

Моторная конструкция

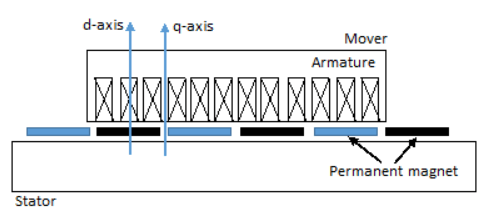
Этот рисунок показывает моторную конструкцию.

Уравнения

Напряжения через обмотки статора заданы:

$[\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}] = [\begin{matrix} R_{s} & 0 & 0 \\ 0 & R_{s} & 0 \\ 0 & 0 & R_{s} \end{matrix}] [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] + [\begin{matrix} \frac{d ψ_{a}}{d t} \\ \frac{d ψ_{b}}{d t} \\ \frac{d ψ_{c}}{d t} \end{matrix}],$

где:

_va, _vb и _vc являются отдельными напряжениями фазы через обмотки статора.
_Rs является эквивалентным сопротивлением каждой обмотки статора.
_ia, _ib и _ic являются токами, текущими в обмотках статора.
$\frac{d ψ_{a}}{d t},$ $\frac{d ψ_{b}}{d t},$ и $\frac{d ψ_{c}}{d t}$ скорости изменения магнитного потока в каждой обмотке статора.

Постоянный магнит и эти три обмотки способствуют общему потоку, соединяющему каждую обмотку. Общий поток задан:

$[\begin{matrix} ψ_{a} \\ ψ_{b} \\ ψ_{c} \end{matrix}] = [\begin{matrix} L_{a a} & L_{a b} & L_{a c} \\ L_{b a} & L_{b b} & L_{b c} \\ L_{c a} & L_{c b} & L_{c c} \end{matrix}] [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] + [\begin{matrix} ψ_{a m} \\ ψ_{b m} \\ ψ_{c m} \end{matrix}],$

где:

_ψa, _ψb и _ψc являются общими потоками, соединяющими каждую обмотку статора.
_Laa, _Lbb и _Lcc являются самоиндукциями обмоток статора.
_Lab, _Lac, _Lba, _Lbc, _Lca и _Lcb являются взаимной индуктивностью обмоток статора.
_ψam, _ψbm и _ψcm являются потоками постоянного магнита, соединяющими обмотки статора.

Индуктивность в обмотках статора является функциями электрического угла и задана:

$θ_{e} = N_{p} x + r o t o r o f f s e t,$

$L_{a a} = L_{s} + L_{m} cos (2 θ_{e}),$

$L_{b b} = L_{s} + L_{m} cos (2 (θ_{e} - 2 π / 3)),$

$L_{c c} = L_{s} + L_{m} cos (2 (θ_{e} + 2 π / 3)),$

$L_{a b} = L_{b a} = - M_{s} - L_{m} \cos (2 (θ_{e} + π / 6)),$

$L_{b c} = L_{c b} = - M_{s} - L_{m} \cos (2 (θ_{e} + π / 6 - 2 π / 3)),$

$L_{c a} = L_{a c} = - M_{s} - L_{m} \cos (2 (θ_{e} + π / 6 + 2 π / 3)),$

где:

_θe является электрическим углом.
rotor offset является 0 если вы задаете ротор электрический угол относительно d-оси или -pi/2 если вы задаете ротор электрический угол относительно q-оси.
$N_{p} = \frac{π}{τ}$ и τ является полярным тангажом.
x является расстоянием.
_Ls является самоиндукцией статора на фазу. Это значение является средней самоиндукцией каждой из обмоток статора.
_Lm является колебанием индуктивности статора. Это значение является колебанием самоиндукции и взаимной индуктивности с изменяющимся углом.
_Ms является статором взаимная индуктивность. Это значение является средней взаимной индуктивностью между обмотками статора.

Поток постоянного магнита, соединяющий извилистый a, является максимумом когда _θe = 0 ° и нуль когда _θe = 90 °. Поэтому соединенный моторный поток задан:

$[\begin{matrix} ψ_{a m} \\ ψ_{b m} \\ ψ_{c m} \end{matrix}] = [\begin{matrix} ψ_{m} \cos θ_{e} \\ ψ_{m} \cos (θ_{e} - 2 π / 3) \\ ψ_{m} \cos (θ_{e} + 2 π / 3) \end{matrix}]$

где _ψm является потокосцеплением постоянного магнита.

Упрощенные электрические уравнения

Применение преобразования Парка к электрическим уравнениям производит выражение для силы, которая независима от угла.

Преобразование парка задано:

$P = 2 / 3 [\begin{matrix} \cos θ_{e} & \cos (θ_{e} - 2 π / 3) & \cos (θ_{e} + 2 π / 3) \\ - \sin θ_{e} & - \sin (θ_{e} - 2 π / 3) & - \sin (θ_{e} + 2 π / 3) \\ 0.5 & 0.5 & 0.5 \end{matrix}]$

где _θe является электрическим углом, заданным как _Npx.

Используя преобразование Парка на статоре извилистые напряжения и токи преобразовывают их в систему координат dq0, которая независима от угла:

$[\begin{matrix} v_{d} \\ v_{q} \\ v_{0} \end{matrix}] = P [\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}]$

$[\begin{matrix} i_{d} \\ i_{q} \\ i_{0} \end{matrix}] = P [\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] .$

Применение преобразования Парка к первым двум электрическим уравнениям производит следующие уравнения, которые задают поведение блока:

$v_{d} = R_{s} i_{d} + L_{d} \frac{d i_{d}}{d t} - N_{p} v i_{q} L_{q},$

$v_{q} = R_{s} i_{q} + L_{q} \frac{d i_{q}}{d t} + N_{p} v (i_{d} L_{d} + ψ_{m}),$

$v_{0} = R_{s} i_{0} + L_{0} \frac{d i_{0}}{d t},$

$F = \frac{3}{2} N_{p} (i_{q} (i_{d} L_{d} + ψ_{m}) - i_{d} i_{q} L_{q}),$

$M \frac{d v}{d t} = F - F_{L} - B_{m} v,$

где:

_Ld = _Ls + _Ms + 3/2 _Lm. _Ld является статором d - составляющая индукции.
_Lq = _Ls + _Ms − 3/2 _Lm. _Lq является статором q - составляющая индукции.
_L0 = _Ls – 2_Ms. _L0 является индуктивностью нулевой последовательности статора.
_Rs является сопротивлением статора на фазу.
v является линейной скоростью.
_Np является полярным фактором тангажа.
M является массой двигателя.
_Bm является затуханием.
_FL является силой загрузки.

Использование блока PMLSM исходная, неортогональная реализация Парка преобразовывает. При попытке применить альтернативную реализацию, вы получаете различные результаты для dq0 напряжения и токов.

Отношение между силой постоянный _kf, коэффициент противо-ЭДС, постоянная _ke, и потокосцеплением постоянного магнита определяется следующим образом:

$k_{e} = k_{f} = N_{p} ψ_{m} .$

Тепловые порты

Блок имеет четыре дополнительных тепловых порта, один для каждой из трех обмоток статора и один для ротора. Эти порты скрыты по умолчанию. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите Show thermal port. Это действие отображает тепловые порты на значке блока и отсоединяет параметры Thermal. Эти параметры описаны далее на этой странице с описанием.

Переменные

Используйте настройки Variables, чтобы задать приоритет и начальные целевые значения для переменных в блоках перед симуляцией. Для получения дополнительной информации смотрите Приоритет Набора и Начальную Цель для Переменных в блоках.

Порты

Сохранение

развернуть все

`~` — Трехфазный порт
электрический

Расширяемый трехфазный порт.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Composite three-phase ports.

`a` — a - фаза
электрический

Электрический порт сохранения, сопоставленный с a - фаза.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Expanded three-phase ports.

`b` — b - фаза
электрический

Электрический порт сохранения, сопоставленный с b - фаза.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Expanded three-phase ports.

`c` — c - фаза
электрический

Электрический порт сохранения, сопоставленный с c - фаза.

Зависимости

Чтобы включить этот порт, установите Electrical connection на Expanded three-phase ports.

`n` — Нейтральная фаза
электрический

Электрический порт сохранения сопоставлен с нейтральной фазой.

Зависимости

Чтобы включить этот порт, установите Winding Type на Wye-wound и Zero sequence к Include.

`R` — Моторный двигатель
механическое устройство

Порт механической передачи сопоставлен с моторным двигателем.

`C` — Моторный случай
механическое устройство

Порт механической передачи сопоставлен с моторным случаем.

`HA` — Обмотка теплового порта
тепловой

Тепловой порт сохранения, сопоставленный с обмоткой A. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите желаемый вариант блока с тепловыми портами. Для получения дополнительной информации смотрите Тепловые Порты.

`HB` — Обмотка B тепловой порт
тепловой

Тепловой порт сохранения, сопоставленный с обмоткой B. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите желаемый вариант блока с тепловыми портами. Для получения дополнительной информации смотрите Тепловые Порты.

`HC` — Обмотка C тепловой порт
тепловой

Тепловой порт сохранения, сопоставленный с обмоткой C. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите желаемый вариант блока с тепловыми портами. Для получения дополнительной информации смотрите Тепловые Порты.

`HR` — Ротор тепловой порт
тепловой

Тепловой порт сохранения сопоставлен с ротором. Чтобы осушить тепловые порты, щелкните правой кнопкой по блоку по своей модели, выберите Simscape> Block choices, и затем выберите желаемый вариант блока с тепловыми портами. Для получения дополнительной информации смотрите Тепловые Порты.

Параметры

развернуть все

Основной

`Electrical connection` — Электрическое соединение
`Composite three-phase ports` (значение по умолчанию) | `Expanded three-phase ports`

Иметь ли составной объект или расширил трехфазные порты.

`Winding type` — Настройка обмоток
`Wye-wound` (значение по умолчанию) | `Delta-wound`

Настройка для обмоток:

Wye-wound — Обмотки являются раной Уая.
Delta-wound — Обмотки являются раной дельты. a - фаза соединяется между портами a и b, b - фазой между портами b и c и c - фаза между портами c и a.

`Modeling fidelity` — Моделирование точности
`Constant Ld, Lq and PM` (значение по умолчанию) | `Tabulated Ld, Lq and PM`

Моделирование точности:

Constant Ld, Lq and PM — Ld, Lq и значения PM являются постоянными и заданы их соответствующими параметрами.
Tabulated Ld, Lq and PM — Ld, Lq и значения PM вычисляются онлайн из текущих интерполяционных таблиц DQ как follows:h

$L_{d} = f_{1} (i_{d}, i_{q})$

$L_{d} = f_{2} (i_{d}, i_{q})$

$λ_{P M} = f_{2} (i_{d}, i_{q})$

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0.

`Polar pitch` — Полярный тангаж
0.03 `m` (значение по умолчанию) | скаляр

Полярный тангаж.

`Permanent magnet flux linkage parameterization` — Параметризация потокосцепления постоянного магнита
`Specify flux linkage` (значение по умолчанию) | `Specify force constant` | `Specify back EMF constant`

Потокосцепление постоянного магнита в виде Specify flux linkage, Specify force constant, или Specify back EMF constant.

`Permanent magnet flux linkage` — Потокосцепление постоянного магнита
0.03 `Wb` (значение по умолчанию) | скаляр

Пиковое потокосцепление постоянного магнита с любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Permanent magnet flux linkage parameterization на Specify flux linkage и Modeling fidelity к Constant Ld, Lq and PM.

`Force constant` — Постоянная сила
0.18 `N/A` (значение по умолчанию) | скаляр

Сила, постоянная для любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Permanent magnet flux linkage parameterization на Specify force constant и Modeling fidelity к Constant Ld, Lq and PM.

`Back EMF constant` — Коэффициент противо-ЭДС, постоянная
0.18 `s*V/m` (значение по умолчанию) | скаляр

Коэффициент противо-ЭДС, постоянная для любой из обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Permanent magnet flux linkage parameterization на Specify back EMF constant и Modeling fidelity к Constant Ld, Lq and PM.

`Stator parameterization` — Параметризация статора
`Specify Ld, Lq, and L0` (значение по умолчанию) | `Specify Ls, Lm, and Ms`

Параметризация статора в виде Specify Ld, Lq, and L0 или Specify Ls, Lm, and Ms.

`Stator d-axis inductance, Ld` — Статор `d`- составляющая индукции
0.00019 `H` (значение по умолчанию) | скаляр

d- составляющая индукции.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Constant Ld, Lq and PM.

`Stator q-axis inductance, Lq` — Q-составляющая-индукции статора
0.00025 `H` (значение по умолчанию) | скаляр

q- составляющая индукции.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Constant Ld, Lq and PM.

`Stator zero-sequence inductance, L0` — Индуктивность нулевой последовательности статора
0.00016 `H` (значение по умолчанию) | скаляр

Индуктивность нулевой последовательности.

Зависимости

Включить этот параметр также:

Установите Winding Type на Wye-wound, Zero sequence к Include, и Stator parameterization к Specify Ld, Lq, and L0.
Установите Winding Type на Delta-wound и Stator parameterization к Specify Ld, Lq, and L0.

`Direct-axis current vector, iD` — Прямая ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию) | вектор

Прямая ось текущий вектор, ID.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld, Lq and PM.

`Quadrature-axis current vector, iQ` — Квадратурная ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию) | вектор

Квадратурная ось текущий вектор, IQ.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld, Lq and PM.

`Ld matrix, Ld(id,iq)` — Матрица Ld
`0.00019 * ones(3, 3)` `H` (значение по умолчанию) | матрица

Матрица Ld.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld, Lq and PM.

`Lq matrix, Lq(id,iq)` — Матрица Lq
`0.00025 * ones(3, 3)` `H` (значение по умолчанию) | матрица

Матрица Lq.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ld, Lq, and L0 и Modeling fidelity к Tabulated Ld, Lq and PM.

`Permanent magnet flux linkage, PM(id,iq)` — Потокосцепление постоянного магнита
`0.03 * ones(3, 3)` `Wb` (значение по умолчанию)

Потокосцепление постоянного магнита.

Зависимости

Чтобы включить этот параметр, установите:

Stator parameterization к Specify Ld, Lq, and L0
Modeling fidelity к Tabulated Ld, Lq and PM
Permanent magnet flux linkage parameterization к Specify flux linkage

`Force constant matrix, kf(iD,iQ)` — Обеспечьте постоянную матрицу
`0.18 * ones(3, 3)` `N/A` (значение по умолчанию) | матрица

Обеспечьте постоянную матрицу.

Зависимости

Чтобы включить этот параметр, установите:

Stator parameterization к Specify Ld, Lq, and L0
Modeling fidelity к Tabulated Ld, Lq and PM
Permanent magnet flux linkage parameterization к Specify force constant

`Back EMF constant matrix, ke(iD,iQ)` — Матрица Коэффициента противо-ЭДС, постоянной
`0.18 * ones(3, 3)` `s*V/m` (значение по умолчанию) | матрица

Матрица Коэффициента противо-ЭДС, постоянной.

Зависимости

Чтобы включить этот параметр, установите:

Stator parameterization к Specify Ld, Lq, and L0
Modeling fidelity к Tabulated Ld, Lq and PM
Permanent magnet flux linkage parameterization к Specify back EMF constant

`Stator self-inductance per phase, Ls` — Самоиндукция статора на фазу
0.0002 `H` (значение по умолчанию) | скаляр

Средняя самоиндукция каждой из пяти обмоток статора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ls, Lm, and Ms.

`Stator inductance fluctuation, Lm` — Колебание индуктивности статора
-0.00002 `H` (значение по умолчанию) | скаляр

Колебание самоиндукции и взаимной индуктивности обмоток статора с углом.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ls, Lm, and Ms.

`Stator mutual inductance, Ms` — Статор взаимная индуктивность
0.00002 `H` (значение по умолчанию) | скаляр

Средняя взаимная индуктивность между обмотками статора.

Зависимости

Чтобы включить этот параметр, установите Stator parameterization на Specify Ls, Lm, and Ms.

`Stator resistance per phase, Rs` — Сопротивление статора на фазу
0.013 `Ohm` (значение по умолчанию) | скаляр

Сопротивление каждой из обмоток статора.

`Zero sequence` — Нулевая опция последовательности
`Include` (значение по умолчанию) | `Exclude`

Опция, чтобы включать или исключить термины нулевой последовательности.

Include — Включайте термины нулевой последовательности. Чтобы приоритизировать точность модели, используйте эту настройку по умолчанию. Используя эту опцию:
- Результаты по ошибке для симуляций, которые используют решатель Разделения. Для получения дополнительной информации смотрите, что Скорость симуляции Увеличения Использует Решатель Разделения.
- Отсоединяет параметр нулевой последовательности.
Exclude — Исключите термины нулевой последовательности. Чтобы приоритизировать скорость симуляции для настольной симуляции или развертывания приложений, выберите эту опцию.

Зависимости

Чтобы включить этот параметр, установите Winding Type на Wye-wound.

`Angle definition` — Контрольная точка для углового измерения
`Angle between the a-phase magnetic axis and the d-axis` (значение по умолчанию) | `Angle between the a-phase magnetic axis and the q-axis`

Контрольная точка для углового измерения. Значением по умолчанию является Angle between the a-phase magnetic axis and the d-axis. Это определение показывают на Моторном рисунке Конструкции. Когда вы выбираете это значение, двигатель и a - потоки фазы выравниваются, когда угол двигателя является нулем.

Другим значением, которое можно выбрать для этого параметра, является Angle between the a-phase magnetic axis and the q-axis. Когда вы выбираете это значение, a - текущая фаза генерирует максимальную силу, когда угол двигателя является нулем.

Механическое устройство

`Mass of the mover` — Масса двигателя
0.01 `kg` (значение по умолчанию)

Масса моторного двигателя.

`Linear damping` — Линейное затухание
0 `N/(m/s)` (значение по умолчанию)

Линейное затухание.

Тепловой

Эти параметры появляются только для блоков с осушенными тепловыми портами. Для получения дополнительной информации смотрите Тепловые Порты.

`Measurement temperature` — Температура измерения
298.15 `K` (значение по умолчанию)

Температура, для которой заключаются в кавычки параметры двигателя.

`Resistance temperature coefficient` — Коэффициент температуры сопротивления
`3.93e-3` `1/K` (значение по умолчанию)

Коэффициент α в сопротивлении связи уравнения температуре, как описано в Тепловой Модели для Блоков Привода. Значение по умолчанию для меди.

`Permanent magnet flux temperature coefficient` — Коэффициент температуры потока постоянного магнита
-0.001 `1/K` (значение по умолчанию)

Дробная скорость изменения плотности потока постоянного магнита с температурой. Используйте этот параметр, чтобы линейно уменьшать крутящий момент и вызванный коэффициент противо-ЭДС, когда температура повышается.

`Thermal mass for each stator winding` — Количество тепла для каждой обмотки статора
100 `J/K` (значение по умолчанию)

Значение количества тепла для A, B, и обмотки C. Количество тепла является энергией, требуемой для повышения температуры на один градус.

`Rotor thermal mass` — Количество тепла ротора
200 `J/K` (значение по умолчанию)

Количество тепла ротора, то есть, энергия, требуемая повысить температуру ротора одной степенью.

Примеры модели

Трехфазный диск PMLSM

Управляйте положением в трехфазном диске постоянного магнита линейной синхронной машины (PMLSM). Подсистема Управления использует основанную на PI структуру каскадного регулирования с тремя циклами управления, внешним циклом управления положения, циклом регулировки скорости и двумя внутренними текущими циклами управления. Управляемый трехфазный конвертер питает PMLSM. Симуляция использует ссылки шага. Подсистема Осциллографов содержит осциллографы, которые позволяют вам видеть результаты симуляции.

Вопросы совместимости

развернуть все

Обновление портов электрического соединения

Поведение изменяется в R2021b

От R2021b вперед, чтобы переключиться между составным объектом и расширенными портами, устанавливают параметр Electrical connection на любой Composite three-phase ports или Expanded three-phase ports.

В результате этих изменений, в модели, сохраненной в более раннем релизе, рассматривают параметр Electrical connection этого блока.

Ссылки

[1] Kundur, P. Устойчивость энергосистемы и управление. Нью-Йорк, Нью-Йорк: Макгроу Хилл, 1993.

[2] Андерсон, пополудни анализ неработающих энергосистем. IEEE нажимает Power Systems Engineering Series, 1995. ISBN 0-7803-1145-0.

[3] С. Чжан и Дж. Пэн. Нелинейное Устойчивое Управление Скользящим режимом для PM Linear Synchronous Motors. 2 006 CES/IEEE 5-я Международная Конференция по Управлению Силовой электроникой и Движением, Шанхай, 2006, стр 1–5.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Введенный в R2020a

Документация

PMLSM

Описание

Моторная конструкция

Уравнения

Упрощенные электрические уравнения

Тепловые порты

Переменные

Порты

Сохранение

~ — Трехфазный порт электрический

Зависимости

a — a - фаза электрический

Зависимости

b — b - фаза электрический

Зависимости

c — c - фаза электрический

Зависимости

n — Нейтральная фаза электрический

Зависимости

R — Моторный двигатель механическое устройство

C — Моторный случай механическое устройство

HA — Обмотка теплового порта тепловой

HB — Обмотка B тепловой порт тепловой

HC — Обмотка C тепловой порт тепловой

HR — Ротор тепловой порт тепловой

Параметры

Основной

Electrical connection — Электрическое соединение Composite three-phase ports (значение по умолчанию) | Expanded three-phase ports

Winding type — Настройка обмоток Wye-wound (значение по умолчанию) | Delta-wound

Modeling fidelity — Моделирование точности Constant Ld, Lq and PM (значение по умолчанию) | Tabulated Ld, Lq and PM

Зависимости

Polar pitch — Полярный тангаж0.03 m (значение по умолчанию) | скаляр

Permanent magnet flux linkage parameterization — Параметризация потокосцепления постоянного магнита Specify flux linkage (значение по умолчанию) | Specify force constant | Specify back EMF constant

Permanent magnet flux linkage — Потокосцепление постоянного магнита0.03 Wb (значение по умолчанию) | скаляр

Зависимости

Force constant — Постоянная сила0.18 N/A (значение по умолчанию) | скаляр

Зависимости

Back EMF constant — Коэффициент противо-ЭДС, постоянная0.18 s*V/m (значение по умолчанию) | скаляр

Зависимости

Stator parameterization — Параметризация статора Specify Ld, Lq, and L0 (значение по умолчанию) | Specify Ls, Lm, and Ms

Stator d-axis inductance, Ld — Статор d- составляющая индукции0.00019 H (значение по умолчанию) | скаляр

Зависимости

Stator q-axis inductance, Lq — Q-составляющая-индукции статора0.00025 H (значение по умолчанию) | скаляр

Зависимости

Stator zero-sequence inductance, L0 — Индуктивность нулевой последовательности статора0.00016 H (значение по умолчанию) | скаляр

Зависимости

Direct-axis current vector, iD — Прямая ось текущий вектор[-200, 0, 200] A (значение по умолчанию) | вектор

Зависимости

Quadrature-axis current vector, iQ — Квадратурная ось текущий вектор[-200, 0, 200] A (значение по умолчанию) | вектор

Зависимости

Ld matrix, Ld(id,iq) — Матрица Ld 0.00019 * ones(3, 3) H (значение по умолчанию) | матрица

Зависимости

Lq matrix, Lq(id,iq) — Матрица Lq 0.00025 * ones(3, 3) H (значение по умолчанию) | матрица

Зависимости

Permanent magnet flux linkage, PM(id,iq) — Потокосцепление постоянного магнита 0.03 * ones(3, 3) Wb (значение по умолчанию)

Зависимости

Force constant matrix, kf(iD,iQ) — Обеспечьте постоянную матрицу 0.18 * ones(3, 3) N/A (значение по умолчанию) | матрица

Зависимости

Back EMF constant matrix, ke(iD,iQ) — Матрица Коэффициента противо-ЭДС, постоянной 0.18 * ones(3, 3) s*V/m (значение по умолчанию) | матрица

Зависимости

Stator self-inductance per phase, Ls — Самоиндукция статора на фазу0.0002 H (значение по умолчанию) | скаляр

Зависимости

Stator inductance fluctuation, Lm — Колебание индуктивности статора-0.00002 H (значение по умолчанию) | скаляр

Зависимости

Stator mutual inductance, Ms — Статор взаимная индуктивность0.00002 H (значение по умолчанию) | скаляр

Зависимости

Stator resistance per phase, Rs — Сопротивление статора на фазу0.013 Ohm (значение по умолчанию) | скаляр

Zero sequence — Нулевая опция последовательности Include (значение по умолчанию) | Exclude

Зависимости

Angle definition — Контрольная точка для углового измерения Angle between the a-phase magnetic axis and the d-axis (значение по умолчанию) | Angle between the a-phase magnetic axis and the q-axis

Механическое устройство

Mass of the mover — Масса двигателя0.01 kg (значение по умолчанию)

Linear damping — Линейное затухание0 N/(m/s) (значение по умолчанию)

Тепловой

Measurement temperature — Температура измерения298.15 K (значение по умолчанию)

Resistance temperature coefficient — Коэффициент температуры сопротивления 3.93e-3 1/K (значение по умолчанию)

Permanent magnet flux temperature coefficient — Коэффициент температуры потока постоянного магнита-0.001 1/K (значение по умолчанию)

Thermal mass for each stator winding — Количество тепла для каждой обмотки статора100 J/K (значение по умолчанию)

Rotor thermal mass — Количество тепла ротора200 J/K (значение по умолчанию)

`~` — Трехфазный порт
электрический

`a` — a - фаза
электрический

`b` — b - фаза
электрический

`c` — c - фаза
электрический

`n` — Нейтральная фаза
электрический

`R` — Моторный двигатель
механическое устройство

`C` — Моторный случай
механическое устройство

`HA` — Обмотка теплового порта
тепловой

`HB` — Обмотка B тепловой порт
тепловой

`HC` — Обмотка C тепловой порт
тепловой

`HR` — Ротор тепловой порт
тепловой

`Electrical connection` — Электрическое соединение
`Composite three-phase ports` (значение по умолчанию) | `Expanded three-phase ports`

`Winding type` — Настройка обмоток
`Wye-wound` (значение по умолчанию) | `Delta-wound`

`Modeling fidelity` — Моделирование точности
`Constant Ld, Lq and PM` (значение по умолчанию) | `Tabulated Ld, Lq and PM`

`Polar pitch` — Полярный тангаж
0.03 `m` (значение по умолчанию) | скаляр

`Permanent magnet flux linkage parameterization` — Параметризация потокосцепления постоянного магнита
`Specify flux linkage` (значение по умолчанию) | `Specify force constant` | `Specify back EMF constant`

`Permanent magnet flux linkage` — Потокосцепление постоянного магнита
0.03 `Wb` (значение по умолчанию) | скаляр

`Force constant` — Постоянная сила
0.18 `N/A` (значение по умолчанию) | скаляр

`Back EMF constant` — Коэффициент противо-ЭДС, постоянная
0.18 `s*V/m` (значение по умолчанию) | скаляр

`Stator parameterization` — Параметризация статора
`Specify Ld, Lq, and L0` (значение по умолчанию) | `Specify Ls, Lm, and Ms`

`Stator d-axis inductance, Ld` — Статор `d`- составляющая индукции
0.00019 `H` (значение по умолчанию) | скаляр

`Stator q-axis inductance, Lq` — Q-составляющая-индукции статора
0.00025 `H` (значение по умолчанию) | скаляр

`Stator zero-sequence inductance, L0` — Индуктивность нулевой последовательности статора
0.00016 `H` (значение по умолчанию) | скаляр

`Direct-axis current vector, iD` — Прямая ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию) | вектор

`Quadrature-axis current vector, iQ` — Квадратурная ось текущий вектор
[-200, 0, 200] `A` (значение по умолчанию) | вектор

`Ld matrix, Ld(id,iq)` — Матрица Ld
`0.00019 * ones(3, 3)` `H` (значение по умолчанию) | матрица

`Lq matrix, Lq(id,iq)` — Матрица Lq
`0.00025 * ones(3, 3)` `H` (значение по умолчанию) | матрица

`Permanent magnet flux linkage, PM(id,iq)` — Потокосцепление постоянного магнита
`0.03 * ones(3, 3)` `Wb` (значение по умолчанию)

`Force constant matrix, kf(iD,iQ)` — Обеспечьте постоянную матрицу
`0.18 * ones(3, 3)` `N/A` (значение по умолчанию) | матрица

`Back EMF constant matrix, ke(iD,iQ)` — Матрица Коэффициента противо-ЭДС, постоянной
`0.18 * ones(3, 3)` `s*V/m` (значение по умолчанию) | матрица

`Stator self-inductance per phase, Ls` — Самоиндукция статора на фазу
0.0002 `H` (значение по умолчанию) | скаляр

`Stator inductance fluctuation, Lm` — Колебание индуктивности статора
-0.00002 `H` (значение по умолчанию) | скаляр

`Stator mutual inductance, Ms` — Статор взаимная индуктивность
0.00002 `H` (значение по умолчанию) | скаляр

`Stator resistance per phase, Rs` — Сопротивление статора на фазу
0.013 `Ohm` (значение по умолчанию) | скаляр

`Zero sequence` — Нулевая опция последовательности
`Include` (значение по умолчанию) | `Exclude`

`Angle definition` — Контрольная точка для углового измерения
`Angle between the a-phase magnetic axis and the d-axis` (значение по умолчанию) | `Angle between the a-phase magnetic axis and the q-axis`

`Mass of the mover` — Масса двигателя
0.01 `kg` (значение по умолчанию)

`Linear damping` — Линейное затухание
0 `N/(m/s)` (значение по умолчанию)

`Measurement temperature` — Температура измерения
298.15 `K` (значение по умолчанию)

`Resistance temperature coefficient` — Коэффициент температуры сопротивления
`3.93e-3` `1/K` (значение по умолчанию)

`Permanent magnet flux temperature coefficient` — Коэффициент температуры потока постоянного магнита
-0.001 `1/K` (значение по умолчанию)

`Thermal mass for each stator winding` — Количество тепла для каждой обмотки статора
100 `J/K` (значение по умолчанию)

`Rotor thermal mass` — Количество тепла ротора
200 `J/K` (значение по умолчанию)

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.