Алгоритм мягкого критика агента (SAC) является онлайновым, методом обучения с подкреплением критика агента вне политики без моделей. Алгоритм SAC вычисляет оптимальную политику, которая максимизирует и долгосрочное ожидаемое вознаграждение и энтропию политики. Энтропия политики является мерой неопределенности политики, учитывая состояние. Более высокое энтропийное значение способствует большему количеству исследования. Максимизация и ожидаемое совокупное долгосрочное вознаграждение и энтропийные балансы и эксплуатация и исследование среды.
Для получения дополнительной информации о различных типах агентов обучения с подкреплением смотрите Агентов Обучения с подкреплением.
Реализация агента SAC в пакете Reinforcement Learning Toolbox™ использует двух критиков Q-функции-ценности, который предотвращает переоценку функции ценности. Другие реализации алгоритма SAC используют дополнительного критика функции ценности.
Агенты SAC могут быть обучены в средах со следующим наблюдением и пространствами действий.
| Пространство наблюдений | Пространство действий |
|---|---|
| Дискретный или непрерывный | Непрерывный |
Агенты SAC используют следующие представления актёра и критика.
| Критик | Агент |
|---|---|
Q критика Q-функции-ценности (S, A), который вы создаете использование | Стохастический π агента политики (S), который вы создаете использование |
Во время обучения, агента SAC:
Обновляет агента и свойства критика равномерно во время изучения.
Оценивает среднее и стандартное отклонение Гауссова вероятностного распределения для непрерывного пространства действий, затем случайным образом выбирает действия на основе распределения.
Обновляет энтропийный термин веса, который балансирует ожидаемый доход и энтропию политики.
Прошлый опыт хранилищ с помощью кругового буфера опыта. Агент обновляет агента и критика, использующего мини-пакет событий, случайным образом произведенных от буфера.
Если UseDeterministicExploitation опция в rlSACAgentOptions установлен в true действие с наибольшим правдоподобием всегда используется в sim и generatePolicyFunction. Это вызывает симулированного агента и сгенерированную политику вести себя детерминировано.
Чтобы оценить политику и функцию ценности, агент SAC обеспечивает следующие функциональные аппроксимации:
Стохастический агент π (S |θ) — агент, параметрами θ, берет наблюдение S и возвращает функцию плотности вероятности действия. Агент случайным образом выбирает действия на основе этой функции плотности.
Один или два критика Q-значения Qk (S, A |ϕk) — критики, каждый параметрами ϕk, берут наблюдение S и действие A как входные параметры и возвращают соответствующее ожидание функции ценности, которая включает и долгосрочное вознаграждение и энтропию.
Один или два целевых критика Qtk (S, A |ϕtk) — Чтобы улучшить устойчивость оптимизации, агент периодически устанавливает целевые параметры критика ϕtk на последние соответствующие значения параметров критика. Количество целевых критиков совпадает с количеством критиков.
Когда вы используете двух критиков, Q 1 (S, A) и Q 2 (S, A), у каждого критика может быть отличная структура. Когда у критиков есть та же структура, у них должны быть различные начальные значения параметров.
Для каждого критика Qk (S, A) и Qtk (S, A) имеет ту же структуру и параметризацию.
Когда обучение завершено, обученная оптимальная политика хранится в агенте π (S).
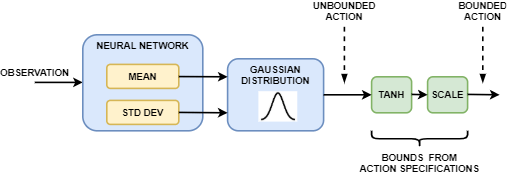
Агент в агенте SAC генерирует среднее и стандартное отклонение выходные параметры. Чтобы выбрать действие, агент сначала случайным образом выбирает неограниченное действие из Распределения Гаусса этими параметрами. Во время обучения агент SAC использует неограниченное вероятностное распределение, чтобы вычислить энтропию политики для заданного наблюдения.
Если пространство действий агента SAC ограничено, агент генерирует ограниченные действия путем применения tanh и операции масштабирования к неограниченному действию.
Можно создать агента SAC с представлениями актёра и критика по умолчанию на основе спецификаций наблюдений и спецификаций действия от среды. Для этого выполните следующие шаги.
Создайте спецификации наблюдений для своей среды. Если у вас уже есть объект интерфейса среды, можно получить эти технические требования использование getObservationInfo.
Технические требования действия по созданию для вашей среды. Если у вас уже есть объект интерфейса среды, можно получить эти технические требования использование getActionInfo.
В случае необходимости задайте количество нейронов в каждом learnable слое или использовать ли рекуррентную нейронную сеть. Для этого создайте объект опции инициализации агента использование rlAgentInitializationOptions.
В случае необходимости задайте опции агента с помощью rlSACAgentOptions объект.
Создайте агента с помощью rlSACAgent объект.
В качестве альтернативы можно создать представления актёра и критика и использовать эти представления, чтобы создать агента. В этом случае гарантируйте, что размерности ввода и вывода представлений актёра и критика совпадают с соответствующим действием и спецификациями наблюдений среды.
Создайте стохастического агента с помощью rlStochasticActorRepresentation объект. Для агентов SAC сеть агента не должна содержать tanhLayer и scalingLayer в среднем выходе path.
Создайте одного или двух критиков, использующих rlQValueRepresentation объекты.
Задайте опции агента с помощью rlSACAgentOptions объект.
Создайте агента с помощью rlSACAgent объект.
Агенты SAC не поддерживают агентов и критиков, которые используют текущие глубокие нейронные сети в качестве функциональных аппроксимаций.
Для получения дополнительной информации о создании агентов и критиков для приближения функций, смотрите, Создают Представления Функции ценности и политика.
Агенты SAC используют следующий алгоритм настройки, в котором они периодически обновляют своего агента и модели критика и энтропийный вес. Чтобы сконфигурировать алгоритм настройки, задайте опции с помощью rlSACAgentOptions объект. Здесь, K = 2 является количеством критиков, и k является индексом критика.
Инициализируйте каждого критика Qk (S, A) со случайными значениями параметров ϕk, и инициализируйте каждого целевого критика теми же случайными значениями параметров: .
Инициализируйте агента π (S) со случайными значениями параметров θ.
Выполните горячий запуск путем взятия последовательности действий после начальной случайной политики в π (S). Для каждого действия сохраните опыт в буфере опыта. Чтобы задать количество нагревают действия, используют NumWarmStartSteps опция.
Для каждого учебного временного шага:
Для текущего наблюдения S выберите действие A с помощью политики в π (S).
Выполните действие A. Наблюдайте вознаграждение R и следующее наблюдение S'.
Сохраните опыт (S, A, R, S') в буфере опыта.
Произведите случайный мини-пакет событий M (Si, Ai, Ri, S'i) от буфера опыта. Чтобы задать M, используйте MiniBatchSize опция.
Каждый DC временные шаги, обновите параметры каждого критика путем минимизации потери Lk через все произведенные события. Чтобы задать DC, используйте CriticUpdateFrequency опция.
Если S'i является конечным состоянием, цель функции ценности, yi равен опыту, вознаграждает Ri. В противном случае цель функции ценности является суммой Ri, минимальным обесцененным будущим вознаграждением от критиков и взвешенной энтропией.
Здесь:
A'i является ограниченным действием, выведенным из неограниченного выхода агента π (S'i).
γ является коэффициентом дисконтирования, который вы задаете использование DiscountFactor опция.
взвешенная энтропия политики для ограниченного выхода агента когда в S состояния. α является энтропийным весом потерь, который вы задаете использование EntropyLossWeight опция.
Каждый DA временные шаги, обновите параметры агента путем минимизации следующей целевой функции. Чтобы установить DA, используйте PolicyUpdateFrequency опция.
Каждый DA временные шаги, также обновите энтропийный вес путем минимизации следующей функции потерь.
Здесь, ℋ является целевой энтропией, которая вы задаете использование EntropyWeightOptions.TargetEntropy опция.
Каждый DT шаги, обновите целевых критиков в зависимости от целевого метода обновления. Чтобы задать DT, используйте TargetUpdateFrequency опция. Для получения дополнительной информации см. Целевые Методы Обновления.
Повторите шаги 4 - 8 времена NG, где NG является количеством шагов градиента, которые вы задаете использование NumGradientStepsPerUpdate опция.
Агенты SAC обновляют свои целевые параметры критика с помощью одного из следующих целевых методов обновления.
Сглаживание — Обновление целевые параметры критика на каждом временном шаге с помощью коэффициента сглаживания τ. Чтобы задать коэффициент сглаживания, используйте TargetSmoothFactor опция.
Периодический — Обновление целевые параметры критика периодически, не сглаживая (TargetSmoothFactor = 1). Чтобы задать период обновления, используйте TargetUpdateFrequency параметр.
Периодическое сглаживание — Обновление целевые параметры периодически со сглаживанием.
Чтобы сконфигурировать целевой метод обновления, создайте rlSACAgentOptions объект и набор TargetUpdateFrequency и TargetSmoothFactor параметры как показано в следующей таблице.
| Метод Update | TargetUpdateFrequency | TargetSmoothFactor |
|---|---|---|
| Сглаживание (значения по умолчанию) | 1 | Меньше чем 1 |
| Периодический | Больше, чем 1 | 1 |
| Периодическое сглаживание | Больше, чем 1 | Меньше чем 1 |
[1] Haarnoja, Tuomas, Аужицк Чжоу, Кристиан Хартикайнен, Джордж Такер, Sehoon Ха, Цзе Тань, Викэш Кумар, и др. "Мягкие Алгоритмы Критика Агента и Приложение". Предварительно распечатайте, представленный 29 января 2019. https://arxiv.org/abs/1812.05905.
rlSACAgent | rlSACAgentOptions