Кратковременное преобразование Фурье глубокого обучения
[ возвращает Кратковременное преобразование Фурье (STFT) глубокого обучения yr,yi] = dlstft(x)x. dlstft требует Deep Learning Toolbox™.
[ задает дополнительные опции с помощью аргументов name-value. Опции включают спектральное окно и длину БПФ. Эти аргументы могут быть добавлены к любому из предыдущих входных синтаксисов. Например, yr,yi] = dlstft(___,Name,Value)'DataFormat','CBT' задает формат данных x как CBT.
Сгенерируйте сигнал, произведенный на уровне 600 Гц в течение 2 секунд. Сигнал состоит из щебета с синусоидально различным содержимым частоты.
fs = 6e2; t = 0:1/fs:2; x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);
Сохраните сигнал в бесформатном массиве глубокого обучения. Вычислите кратковременное преобразование Фурье сигнала. Введите шаг расчета как duration скаляр. (В качестве альтернативы введите частоту дискретизации в виде числа.) Указывают, что входной массив находится в 'CTB' формат.
dlx = dlarray(x); [yr,yi,f,t] = dlstft(dlx,seconds(1/fs),'DataFormat','CTB');
Преобразуйте выходные параметры в числовые массивы. Вычислите величину кратковременного преобразования Фурье и отобразите его как график водопада.
yr = extractdata(yr); yi = extractdata(yi); f = extractdata(f); t = seconds(t); waterfall(f,t,squeeze(hypot(yr,yi))') ax = gca; ax.XDir = 'reverse'; view(30,45) ylabel('Time (s)') xlabel('Frequency (Hz)') zlabel('Magnitude')

Сгенерируйте 3 160 (-by-1) массив, содержащий один пакет синусоидального сигнала с 160 выборками, с тремя каналами. Нормированные частоты синусоиды рад/отсчет, рад/отсчет, и рад/отсчет. Сохраните сигнал как dlarray, определение размерностей в порядке. dlarray переставляет измерения массива к 'CBT' форма ожидается нейронной сетью для глубокого обучения. Отобразите размеры измерения массива.
x = dlarray(cos(pi.*(1:3)'/4*(0:159)),'CTB');
[nchan,nbtch,nsamp] = size(x)nchan = 3
nbtch = 1
nsamp = 160
Вычислите кратковременное преобразование Фурье глубокого обучения сигнала. Задайте прямоугольное окно с 64 выборками и длину БПФ 1 024.
[re,im,f,t] = dlstft(x,'Window',rectwin(64),'FFTLength',1024);
dlstft вычисляет преобразование вдоль 'T' размерность. Выходные массивы находятся в 'SCBT' формат. 'S' размерность соответствует частоте в кратковременном преобразовании Фурье.
Извлеките данные из массивов глубокого обучения.
re = squeeze(extractdata(re)); im = squeeze(extractdata(im)); f = extractdata(f); t = extractdata(t);
Вычислите величину кратковременного преобразования Фурье. Постройте величину отдельно для каждого канала в графике водопада.
z = abs(re + 1j*im); for kj = 1:nchan subplot(nchan,1,kj) waterfall(f/pi,t,squeeze(z(:,kj,:))') view(30,45) end xlabel('Frequency (\times\pi rad/sample)') ylabel('Samples')

x — Входной массивdlarray возразите | числовой массивВходной массив в виде бесформатного dlarray (Deep Learning Toolbox), отформатированный dlarray в 'CBT' формат или числовой массив. Если x бесформатный dlarray или числовой массив, необходимо задать 'DataFormat' как некоторое сочетание 'CBT'.
Пример: dlarray(cos(pi./[4;2]*(0:159)),'CTB') и dlarray(cos(pi./[4;2]*(0:159))','TCB') оба задают одно пакетное наблюдение за двухканальной синусоидой в 'CBT' формат.
fs — Частота дискретизацииЧастота дискретизации в виде положительного числового скаляра.
ts Размер шагаduration скалярШаг расчета в виде duration скаляр. Определение ts эквивалентно установке частоты дискретизации f s = 1/ts.
Пример: seconds(1) duration скаляр, представляющий различие с 1 вторым разом между последовательными выборками сигнала.
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'Window',hamming(100),'OverlapLength',50,'FFTLength',128 окна данные с помощью Окна Хэмминга с 100 выборками, с 50 выборками перекрытия между смежными сегментами и БПФ с 128 точками.DataFormat — Формат данных входаФормат данных входа в виде вектора символов или строкового скаляра. Этот аргумент допустим только если x восстанавливается после форматирования.
Каждый символ в этом аргументе должен быть одной из этих меток:
C — Канал
B — Пакетные наблюдения
T Время
dlstft функция принимает любое сочетание 'CBT'. Можно задать самое большее один из каждого CB, и T метки.
Каждый элемент аргумента помечает соответствующую размерность x. Если аргумент не находится в перечисленном порядке ('C' сопровождаемый 'B' и так далее), затем dlstft неявно переставляет и аргумент и данные, чтобы совпадать с порядком, но не изменяясь, как данные хранятся.
Пример: 'CBT'
Window — Спектральное окноhann(128,'periodic') (значение по умолчанию) | векторСпектральное окно в виде вектора. Если вы не задаете окно или задаете его как пустой, функция использует окно Hann длины 128. Длина 'Window' должен быть больше или быть равен 2.
Для списка доступных окон смотрите Windows.
Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Hann длины N + 1.
Типы данных: double | single
OverlapLength — Количество перекрытых выборокКоличество перекрытых выборок в виде неотрицательного целого числа, меньшего, чем длина 'Window'. Если вы не используете 'OverlapLength' или задайте его как пустой, это установлено в самое большое целое число меньше чем 75% длины окна, которая является 96 выборками для окна Hann по умолчанию.
Типы данных: double | single
FFTLength — Количество точек дискретного преобразования Фурье (ДПФ)Количество ДПФ указывает в виде положительного целого числа. Значение должно быть больше или быть равно длине окна. Если длина входного сигнала меньше длины ДПФ, данные дополнены нулями.
Типы данных: double | single
yr, yi — Кратковременное преобразование Фурьеdlarray объекты | восстановили после форматирования dlarray объектыКратковременное преобразование Фурье, возвращенное как два отформатированных dlarray (Deep Learning Toolbox) объекты. yr содержит действительную часть преобразования. yi содержит мнимую часть преобразования.
Если x отформатированный dlarray, yr и yi 'SCBT' отформатированный dlarray объекты. 'S' размерность соответствует частоте в кратковременном преобразовании Фурье.
Если x бесформатный dlarray или числовой массив, yr и yi восстановленный после форматирования dlarray объекты. Порядок размерности в yr и yi 'SCBT'.
Если никакая информация времени не указана, то STFT вычисляется в области значений Найквиста [0, π] если 'FFTLength' является четным и по [0, π), если 'FFTLength' является нечетным. Если вы указываете информацию времени, то интервалы [0, f s/2] и [0, f s/2), соответственно, где f s является эффективной частотой дискретизации.
f — Частотыdlarray объектЧастоты, на которых глубокое обучение вычисляется STFT, возвратились как dlarray объект.
Если входной массив не содержит информацию времени, то частоты находятся в нормированных единицах рад/отсчета.
Если входной массив содержит информацию времени, то f содержит частоты, описанные в Гц.
t \timesdlarray возразите | duration массивВремена, в которые глубокое обучение вычисляется STFT, возвратились как dlarray возразите или duration массив.
Если вы не указываете информацию времени, то t содержит демонстрационные числа.
Если вы задаете частоту дискретизации, то t содержит временные стоимости в секундах.
Если вы задаете шаг расчета, то t duration массив с тем же форматом времени как x.
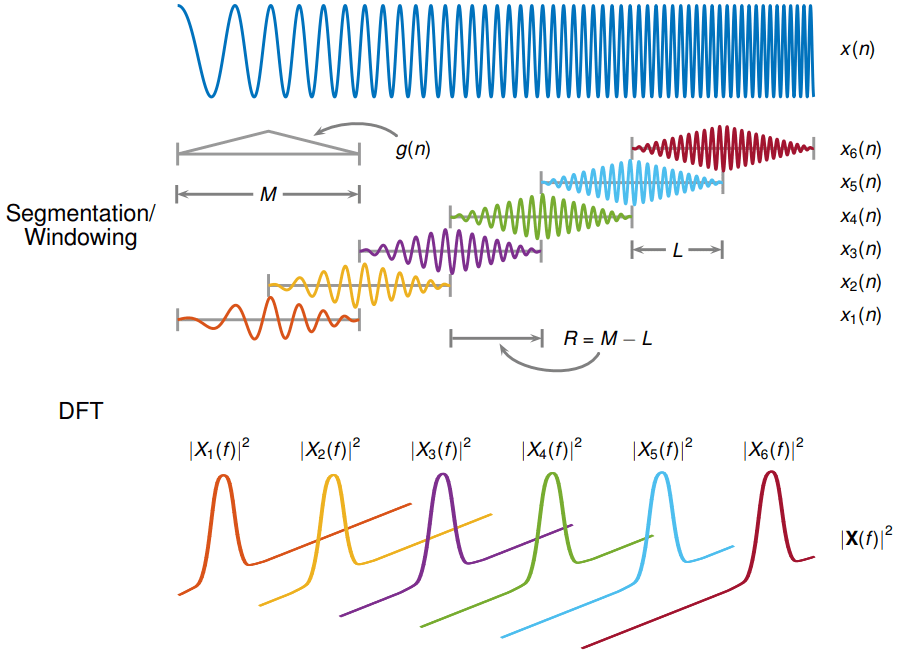
Кратковременное преобразование Фурье (STFT) используется, чтобы анализировать, как содержимое частоты неустановившегося сигнала изменяется в зависимости от времени.
STFT сигнала вычисляется путем скольжения analysis window длины по сигналу и вычислению дискретного преобразования Фурье оконных данных. Окно скачкообразно двигается по исходному сигналу с промежутками в выборки. Функции окна Most сужаются в ребрах, чтобы избежать спектрального вызова. Если ненулевая длина перекрытия задан, добавление перекрытия, которое оконные сегменты компенсируют затухание сигнала в ребрах окна. ДПФ каждого оконного сегмента добавляется к матрице, которая содержит величину и фазу для каждого момента времени и частоты. Количеством столбцов в матрице STFT дают
где длина исходного сигнала и ⌊⌋ символы обозначают функцию пола. Количество строк в матрице равняется ДПФ N, количеству точек ДПФ, для и двухсторонних преобразований в центре и ⌊NDFT/2 ⌋ + 1 для односторонних преобразований.
Матрицей STFT дают таким образом, что элемент th этой матрицы
где
— Функция окна длины .
— ДПФ оконных данных сосредоточен во время .
— Скачкообразно переместите размер между последовательными ДПФ, размер транзитного участка является различием между длиной окна и длина перекрытия .
Величина, в квадрате из STFT, уступает spectrogram представление спектральной плотности мощности функции.
Эта функция полностью поддерживает массивы графического процессора. Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
dlarray (Deep Learning Toolbox) | stft | istft | stftmag2sig | stftLayer
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.