Функция Statistics and Machine Learning Toolbox™ ecdf производит эмпирическую совокупную опасность, оставшегося в живых и кумулятивные функции распределения при помощи Каплана-Мейера непараметрический метод. Средство оценки Каплана-Мейера для функции оставшегося в живых также называется средством оценки предела продукта.
Метод Каплана-Мейера использует данные о выживании, полученные в итоге в таблицах продолжительности жизни. Таблицы продолжительности жизни заказывают данные согласно возрастающим временам отказа, но вы не должны вводить времена отказа/выживания в упорядоченный способ, чтобы использовать ecdf.
Таблица продолжительности жизни обычно состоит из:
Времена отказа
Количество элементов перестало работать во время/период времени
Количество элементов подвергается цензуре во время/период времени
Количество элементов в опасности в начале времени/периода времени
Номер в опасности является общим количеством оставшихся в живых в начале каждого периода. Номер в опасности в начале первого периода является всеми индивидуумами в пожизненном исследовании. В начале каждого оставшегося срока количество в опасности сокращено количеством отказов плюс индивидуумы, подвергнутые цензуре в конце предыдущего периода.
Эта таблица продолжительности жизни показывает фиктивные данные о выживании. В начале первого раза отказа в опасности существует семь элементов. Во время 4, три перестали работать. Таким образом в начале времени 7, в опасности существует четыре элемента. Только один сбой во время 7, таким образом, номер в опасности в начале времени 11 равняется трем. Два перестали работать во время 11, таким образом, в начале времени 12, номер в опасности является тем. Остающийся элемент перестал работать во время 12.
| Время отказа (t) | Не пройдено номер | Номер в опасности |
|---|---|---|
| 4 | 3 | 7 |
| 7 | 1 | 4 |
| 11 | 2 | 3 |
| 12 | 1 | 1 |
Можно оценить опасность, совокупную опасность, выживание и кумулятивные функции распределения с помощью таблиц продолжительности жизни, аналогичных описанному затем.
Совокупный показатель риска (интенсивность отказов)
Показатель риска в каждый период является количеством отказов в установленном сроке, разделенном на количество выживающих индивидуумов в начале периода (номер в опасности).
| Время отказа (t) | Показатель риска (h (t)) | Совокупный показатель риска |
|---|---|---|
| 0 | 0 | 0 |
| t1 | d 1/r1 | d 1/r1 |
| t2 | d 2/r2 | h (t 1) + d 2/r2 |
| ... | ... | ... |
| t n | d n/rn | h (t n – 1) + dn/rn |
Вероятность выживания
В течение каждого периода вероятность выживания является продуктом дополнения показателей риска. Начальная вероятность выживания в начале первого периода времени равняется 1. Если показателем риска в течение каждого периода является h (t i), то вероятность оставшегося в живых как показано.
| Время (t) | Вероятность выживания (S (t)) |
|---|---|
| 0 | 1 |
| t1 | 1* (1 – h (t 1)) |
| t2 | S (t 1) * (1 – h (t 2)) |
| ... | ... |
| t n | S (t n – 1) * (1 – h (t n)) |
Кумулятивная функция распределения
Поскольку кумулятивная функция распределения (cdf) и функция оставшегося в живых являются дополнениями друг друга, можно найти cdf из таблиц продолжительности жизни с помощью F (t) = 1 – S (t).
Можно вычислить совокупный показатель риска, выживаемость и кумулятивную функцию распределения для симулированных данных в первой таблице на этой странице можно следующим образом.
| t | Номер, не пройдено (d) | Номер, подверженный риску (r) | Показатель риска | Вероятность выживания | Кумулятивная функция распределения |
|---|---|---|---|---|---|
| 4 | 3 | 7 | 3/7 | 1 – 3/7 = 4/7 = 0.5714 | 0.4286 |
| 7 | 1 | 4 | 1/4 | 4/7*(1 – 1/4) = 3/7 = .4286 | 0.5714 |
| 11 | 2 | 3 | 2/3 | 3/7*(1 – 2/3) = 1/7 = 0.1429 | 0.8571 |
| 12 | 1 | 1 | 1/1 | 1/7*(1 – 1) = 0 | 1 |
Это оценивает в этом примере, основаны на дискретных временах отказа, и следовательно вычисления не обязательно следуют основанному на производной определению в том, Что такое Анализ Выживания?
Вот то, как можно ввести данные и вычислить эти меры с помощью ecdf. Данные должны не обязательно быть в порядке возрастания. Предположим, что времена отказа хранятся в массиве y.
y = [4 7 11 12];
freq = [3 1 2 1];
[f,x] = ecdf(y,'frequency',freq)f =
0
0.4286
0.5714
0.8571
1.0000
x =
4
4
7
11
12Когда вы подвергли цензуре данные, таблица продолжительности жизни может быть похожей на следующее:
| Время (t) | Номер перестал работать (d) | Цензурирование | Номер, подверженный риску (r) | Показатель риска | Вероятность выживания | Кумулятивная функция распределения |
|---|---|---|---|---|---|---|
| 4 | 2 | 1 | 7 | 2/7 | 1 – 2/7 = 0.7143 | 0.2857 |
| 7 | 1 | 0 | 4 | 1/4 | 0.7143*(1 – 1/4) = 0.5357 | 0.4643 |
| 11 | 1 | 1 | 3 | 2/3 | 0.5357*(1 – 1/3) = 0.3571 | 0.6429 |
| 12 | 1 | 0 | 1 | 1/1 | 0.3571*(1 – 1) = 0 | 1.0000 |
В любой момент времени подвергнутые цензуре элементы также рассматриваются в общем количестве номера в опасности, и формула показателя риска основана на отказавшем номере и общее количество в опасности. При обновлении номера в опасности в начале каждого периода, общее количество привело к сбою и подвергло цензуре в предыдущий период, уменьшается от номера в опасности в начале того периода.
При использовании ecdf, необходимо также ввести информацию о цензурировании с помощью массива бинарных переменных. Войдите 1 для подвергнутых цензуре данных и войдите 0 в течение точного времени отказа.
y = [4 4 4 7 11 11 12];
cens = [0 1 0 0 1 0 0];
[f,x] = ecdf(y,'censoring',cens)f =
0
0.2857
0.4643
0.6429
1.0000
x =
4
4
7
11
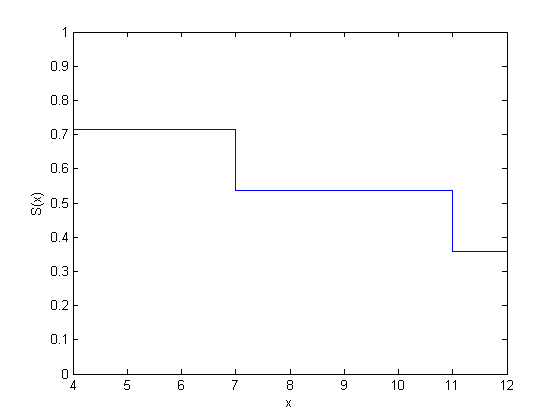
12ecdf, по умолчанию, производит значения кумулятивной функции распределения. Необходимо задать функцию оставшегося в живых или функцию опасности использование дополнительных аргументов пары "имя-значение". Можно также построить результаты можно следующим образом.
figure() ecdf(y,'censoring',cens,'function','survivor');
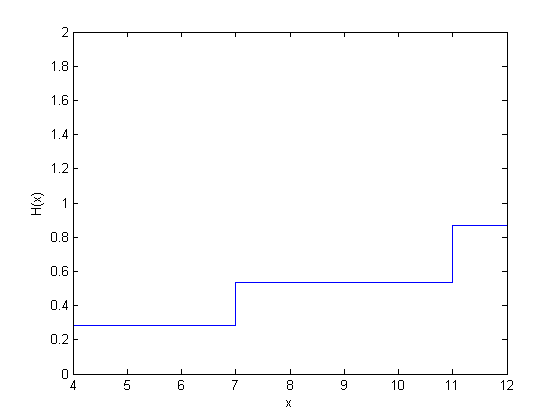
figure() ecdf(y,'censoring',cens,'function','cumulative hazard');
[1] Cox, D. R. и Д. Оукс. Анализ данных о выживании. Лондон: Chapman & Hall, 1984.
[2] Беззаконный, J. F. Статистические модели и методы для пожизненных данных. Хобокен, NJ: Wiley-межнаука, 2002.
[3] Kleinbaum, D. G. и М. Клейн. Анализ выживания. Статистика для Биологии и здоровья. 2-й выпуск. Спрингер, 2005.