swt2

Дискретный стационарный 2D вейвлет преобразовывает

свернуть все на странице

    Синтаксис

    [A,H,V,D] = swt2(X,N,wname)
    [A,H,V,D] = swt2(X,N,LoD,HiD)
    swc = swt2(___)

    Описание

    пример

    [A,H,V,D] = swt2(X,N,wname) возвращает коэффициенты приближения A и горизонталь, вертикальные, и диагональные коэффициенты детали HV, и D, соответственно, стационарного 2D разложения вейвлета изображения X на уровне N использование вейвлета wname.

    Примечание

    • swt2 использование периодическое расширение.

    • swt2 использование арифметика с двойной точностью внутренне и возвращает содействующие матрицы с двойной точностью. swt2 предупреждает, если существует потеря точности при преобразовании, чтобы удвоиться.

    [A,H,V,D] = swt2(X,N,LoD,HiD) использует заданный lowpass, и highpass разложение вейвлета фильтрует LoD и HiD, соответственно.

    swc = swt2(___) возвращает приближение и коэффициенты детали в swc.

    Примеры

    свернуть все

    Скрипт Open Live Script

    Загрузите и отобразите изображение.

    load woman
imagesc(X)
colormap(map)
title('Original')

    Figure contains an axes object. The axes object with title Original contains an object of type image.

    Выполните стационарное разложение вейвлета изображения на уровне 2 с помощью db6. 

    [ca,chd,cvd,cdd] = swt2(X,2,'db6');

    Извлеките приближение уровня 1 и уровня 2 и детализируйте коэффициенты от разложения.

    A1 = wcodemat(ca(:,:,1),255);
H1 = wcodemat(chd(:,:,1),255);
V1 = wcodemat(cvd(:,:,1),255);
D1 = wcodemat(cdd(:,:,1),255);

A2 = wcodemat(ca(:,:,2),255);
H2 = wcodemat(chd(:,:,2),255);
V2 = wcodemat(cvd(:,:,2),255);
D2 = wcodemat(cdd(:,:,2),255);

    Отобразите приближение и детализируйте коэффициенты от этих двух уровней.

    subplot(2,2,1)
imagesc(A1)
title('Approximation Coef. of Level 1')

subplot(2,2,2)
imagesc(H1)
title('Horizontal Detail Coef. of Level 1')

subplot(2,2,3)
imagesc(V1)
title('Vertical Detail Coef. of Level 1')

subplot(2,2,4)
imagesc(D1)
title('Diagonal Detail Coef. of Level 1')

    Figure contains 4 axes objects. Axes object 1 with title Approximation Coef. of Level 1 contains an object of type image. Axes object 2 with title Horizontal Detail Coef. of Level 1 contains an object of type image. Axes object 3 with title Vertical Detail Coef. of Level 1 contains an object of type image. Axes object 4 with title Diagonal Detail Coef. of Level 1 contains an object of type image.

    subplot(2,2,1)
imagesc(A2)
title('Approximation Coef. of Level 2')

subplot(2,2,2)
imagesc(H2)
title('Horizontal Detail Coef. of Level 2')

subplot(2,2,3)
imagesc(V2)
title('Vertical Detail Coef. of Level 2')

subplot(2,2,4)
imagesc(D2)
title('Diagonal Detail Coef. of Level 2')

    Figure contains 4 axes objects. Axes object 1 with title Approximation Coef. of Level 2 contains an object of type image. Axes object 2 with title Horizontal Detail Coef. of Level 2 contains an object of type image. Axes object 3 with title Vertical Detail Coef. of Level 2 contains an object of type image. Axes object 4 with title Diagonal Detail Coef. of Level 2 contains an object of type image.

    Скрипт Open Live Script

    В этом примере показано, как получить одноуровневые и многоуровневые стационарные разложения вейвлета изображения RGB.

    Загрузите и просмотрите изображение RGB. Изображение является трехмерным массивом типа uint8. Начиная с swt2 требует, чтобы первые и вторые измерения оба были делимыми степенью 2, извлекли фрагмент изображения.

    imdata = imread('ngc6543a.jpg');
x = imdata(1:512,1:512,:);
image(x)
title('RGB Image')

    Figure contains an axes object. The axes object with title RGB Image contains an object of type image.

    Получите уровень 4 стационарное разложение вейвлета изображения с помощью db4 вейвлет. Возвратите коэффициенты приближения. Отметьте размерности содействующего массива.

    [a,~,~,~] = swt2(x,4,'db4');
size(a)
    ans = 1×4

   512   512     3     4

    Коэффициенты все имеют тип double. В массиве RGB типа double, каждый компонент цвета является значением между 0 и 1. Перемасштабируйте коэффициенты приближения уровня 2 к значениям между 0 и 1 и просмотрите результат.

    a2 = a(:,:,:,2);
a2 = (a2-min(a2(:)))/(max(a2(:))-min(a2(:)));
image(a2)
title('Level 2 Approximation')

    Figure contains an axes object. The axes object with title Level 2 Approximation contains an object of type image.

    Получите одноуровневое стационарное разложение вейвлета изображения с помощью db4 вейвлет. Возвратите коэффициенты приближения. В одноуровневом разложении изображения RGB третья размерность является одиночным элементом.

    [a,~,~,~] = swt2(x,1,'db4');
size(a)
    ans = 1×4

   512   512     1     3

    Просмотрите коэффициенты приближения. Предотвратить ошибку при использовании image, сожмите содействующий массив приближения, чтобы удалить одноэлементную размерность.

    a2 = squeeze(a);
a2 = (a2-min(a(:)))/(max(a(:))-min(a(:)));
image(a2)
title('Approximation')

    Figure contains an axes object. The axes object with title Approximation contains an object of type image.

    Входные параметры

    свернуть все

    Введите изображение в виде 2D матричного или трехмерного массива с действительным знаком с действительным знаком. Если X 3-D, X принят, чтобы быть изображением RGB, также называемым изображением истинного цвета и третьей размерностью X должен равняться 3. Для получения дополнительной информации об изображениях истинного цвета смотрите Типы изображения.

    Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

    Уровень разложения в виде положительного целого числа. 2N должен разделить size(X,1) и size(X,2)Использование wmaxlev определить максимальный уровень разложения.

    Анализ вейвлета в виде вектора символов или строкового скаляра. swt2 поддержки только (ортогональный) Тип 1 или Тип 2 (биоортогональные) вейвлеты. Смотрите wfilters для списка ортогональных и биоортогональных вейвлетов.

    Разложение вейвлета фильтрует в виде пары ровной длины векторы с действительным знаком. LoD фильтр разложения lowpass и HiD highpass фильтр разложения. Длины LoD и HiD должно быть равным. Смотрите wfilters для получения дополнительной информации.

    Выходные аргументы

    свернуть все

    Коэффициенты приближения, возвращенные как многомерный массив. Размерности A зависьте от размерностей входа X и уровень разложения N.

    • Если X m-by-n:

      • Если N больше 1, затем A m-by-n-by-N. Для 1 ≤ i ≤ N, A(:,:,i) содержит коэффициенты приближения на уровне i.

      • Если N равно 1, затем A m-by-n.

    • Если X m-by-n-by-3:

      • Если N больше 1, затем A m-by-n-by-3-by-N. Для 1 ≤ i ≤ N и j = 1, 2, 3, A(:,:,j,i) содержит коэффициенты приближения на уровне i.

      • Если N равно 1, затем A m-by-n-by-1-by-3. Начиная с MATLAB® удаляет одиночный элемент последние размерности по умолчанию, третья размерность является одиночным элементом.

    Типы данных: double

    Детализируйте коэффициенты, возвращенные как многомерные массивы равного размера. HV, и D содержите горизонталь, вертикальные, и диагональные коэффициенты детали, соответственно. Размерности массивов зависят от размерностей входа X и уровень разложения N.

    • Если X m-by-n:

      • Если N больше 1, массивами является m-by-n-by-N. Для 1 ≤ i ≤ N, H(:,:,i)vi , и D(:,:,i) содержите коэффициенты детали на уровне i.

      • Если N равно 1, массивами является m-by-n.

    • Если X m-by-n-by-3:

      • Если N больше 1, массивами является m-by-n-by-3-by-N. Для 1 ≤ i ≤ N и j = 1, 2, 3, H(:,:,j,i), V(:,:,j,i), и D(:,:,j,i) содержите коэффициенты детали на уровне i.

      • Если N равно 1, массивами является m-by-n-by-1-by-3. Для j = 1, 2, 3, H(:,:,1,j), V(:,:,1,j) и D(:,:,1,j) содержите коэффициенты детали. Поскольку MATLAB удаляет одиночный элемент последние размерности по умолчанию, третья размерность является одиночным элементом.

    Типы данных: double

    Стационарное разложение вейвлета, возвращенное как многомерный массив. swc конкатенация коэффициентов приближения A и детализируйте коэффициенты HV, и D.

    • Если X m-by-n и N больше 1, затем swc = cat(3,H,V,D,A(:,:,N)).

    • Если X m-by-n и N равно 1, затем swc = cat(3,H,V,D,A).

    • Если X m-by-n-by-3 и N больше 1, затем swc = cat(4,H,V,D,A(:,:,:,N)).

    • Если X m-by-n-by-3 и N равный to1, затем swc = cat(4,H,V,D,A).

    Алгоритмы

    свернуть все

    2D дискретный стационарный вейвлет преобразовывает

    Для изображений алгоритм стационарного вейвлета преобразовывает (SWT), похожий на одномерный случай, возможен для двумерных вейвлетов и масштабирующихся функций, полученных из одномерных функций продуктом тензора. Этот вид двумерного SWT приводит к разложению коэффициентов приближения на уровне j на четыре компонента: приближение на уровне j +1 и детали в трех ориентациях (горизонталь, вертикальная, и диагональная).

    Этот график описывает основной шаг разложения для изображений.

    где

    • — Примените операцию свертки к строкам записи с фильтром X.

    • — Примените операцию свертки к столбцам записи с фильтром X.

    Инициализация

    • cA 0 = s

    • F 0 = LoD

    • G 0 = HiD

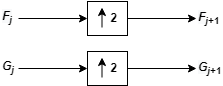
    • где обозначает, сверхдискретизировали.

    Обратите внимание на то, что размер (cAj) = размер (cDj(h)) = размер (cDj(v)) = размер (cDj(d)) = s, где s равняется размеру анализируемого изображения.

    Массивы коэффициентов истинного цвета изображений

    Чтобы отличить одноуровневое разложение изображения истинного цвета от многоуровневого разложения индексируемого изображения, приближение и детализировать массивы коэффициентов изображений истинного цвета является 4-D массивами.

    • Если вы выполняете многоуровневое разложение, размерности AHV, и D m-by-n-by-3-by-k, где k является уровнем разложения.

    • Если вы выполняете одноуровневое разложение, размерности AHV, и D m-by-n-by-1-by-3. Поскольку MATLAB удаляет одиночный элемент последние размерности по умолчанию, третья размерность массивов является одиночным элементом.

    Вопросы совместимости

    развернуть все

    Поведение изменяется в R2017b

    Ссылки

    [1] Нэзон, G. P. и Б. В. Сильверман. “Стационарное Преобразование Вейвлета и Некоторые Статистические Приложения”. В Вейвлетах и Статистике, отредактированной Анестисом Антониэдисом и Жоржем Оппенхеймом, 103:281–99. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_17.

    [2] Койфман, R. R. и Д. Л. Донохо. “Инвариантное переводом Шумоподавление”. В Вейвлетах и Статистике, отредактированной Анестисом Антониэдисом и Жоржем Оппенхеймом, 103:125–50. Нью-Йорк, Нью-Йорк: Спрингер Нью-Йорк, 1995. https://doi.org/10.1007/978-1-4612-2544-7_9.

    [3] Pesquet, J.-C., Х. Крим и Х. Карфэнтэн. “Независимые от времени Ортонормированные Представления Вейвлета”. Транзакции IEEE на Обработке сигналов 44, № 8 (август 1996): 1964–70. https://doi.org/10.1109/78.533717.

    Расширенные возможности

    Смотрите также

    | |

    Представлено до R2006a

    Документация Wavelet Toolbox

    Поддержка

    Для просмотра документации необходимо авторизоваться на сайте