Пользовательский интерфейс Basic Fitting MATLAB® позволяет вам в интерактивном режиме:
Данные модели с помощью сплайна interpolant, сохранение формы interpolant или многочлен до десятого градуса
Постройте график один или несколько совмещается с данными
Постройте график невязок соответствий
Вычислите образцовые коэффициенты
Вычислите норму невязок (статистическая величина, которую можно использовать, чтобы анализировать, как хорошо модель соответствует данным),
Используйте модель, чтобы интерполировать или экстраполировать за пределами данных
Сохраните коэффициенты и вычисленные значения к MATLAB workspace для использования за пределами диалогового окна
Сгенерируйте код MATLAB, чтобы повторно вычислить соответствия и воспроизвести графики с новыми данными
Пользовательский интерфейс Basic Fitting только доступен для 2D графиков. Для более усовершенствованного подбора кривой и регрессионного анализа, смотрите Аппроксимирование кривыми документация Toolbox™ и Статистика и Машинное обучение документация Toolbox™.
Пользовательский интерфейс Basic Fitting сортирует ваши данные в порядке возрастания перед подбором кривой. Если ваш набор данных будет большим, и значения не сортируются в порядке возрастания, у Пользовательского интерфейса Basic Fitting займет больше времени предварительно обработать ваши данные перед подбором кривой.
Можно ускорить Пользовательский интерфейс Basic Fitting первой сортировкой данных. Чтобы создать отсортированные векторы x_sorted и y_sorted от векторов данных x и y, используйте функцию sort MATLAB:
[x_sorted, i] = sort(x); y_sorted = y(i);
Чтобы использовать Пользовательский интерфейс Basic Fitting, необходимо сначала отобразить данные на графике в окне фигуры, с помощью любого MATLAB, строящего график команды, которая производит (только) данные x и y.
Чтобы открыть Пользовательский интерфейс Basic Fitting, выберите Tools> Basic Fitting из меню наверху окна фигуры.
Когда вы полностью расширяете его, дважды кликая по кнопке стрелки![]() в правом нижнем углу, окно отображает три панели. Используйте эти панели для:
в правом нижнем углу, окно отображает три панели. Используйте эти панели для:
Выберите опции графического изображения и модель
Исследуйте и коэффициенты модели экспорта и нормы невязок
Исследуйте и экспорт интерполированные и экстраполируемые значения.
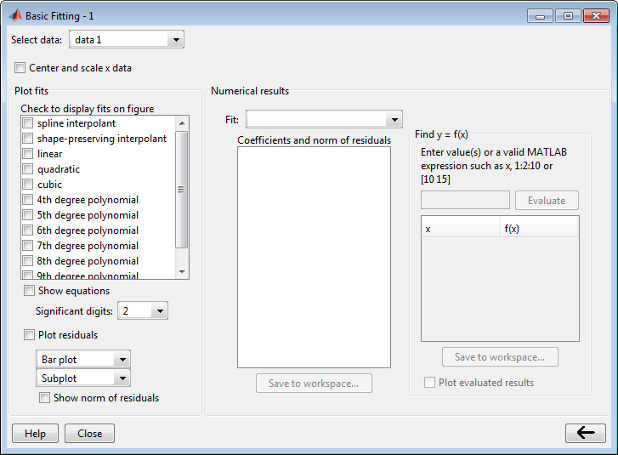
Чтобы расширить или свернуть панели один за другим, кликните по кнопке стрелки в правом нижнем углу интерфейса.
Этот пример показывает, как использовать Пользовательский интерфейс Basic Fitting, чтобы соответствовать, визуализировать, анализировать, сохранить и сгенерировать код для параболических регрессий.
Предсказание данных переписи с соответствием кубического полинома
Узнать, как основной подходящий инструмент вычисляет соответствия
Файл, census.mat, содержит данные о населении U.S. в течение лет 1790 - 1990 в 10-летних интервалах.
Чтобы загрузить и отобразить данные на графике, введите следующие команды в посдказке MATLAB:
load census plot(cdate,pop,'ro')
Команда load добавляет следующие переменные к MATLAB workspace:
cdate — Вектор - столбец, содержащий годы от 1 790 до 1990 в инкрементах 10. Это - переменная прогноза.
pop — Вектор - столбец с населением U.S. в течение каждого года в cdate. Это - переменная отклика.
Векторы данных сортируются в порядке возрастания к году. График показывает население как функцию года.
Теперь вы готовы соответствовать уравнению данные к приросту населения модели в зависимости от времени.
Откройте диалоговое окно Basic Fitting путем выбора Tools> Basic Fitting in the Figure window.
В области соответствий Графика диалогового окна Basic Fitting установите кубический флажок, чтобы соответствовать кубическому полиному к данным.
MATLAB использует ваш выбор, чтобы соответствовать данным и добавляет кубическую линию регрессии к графику можно следующим образом.
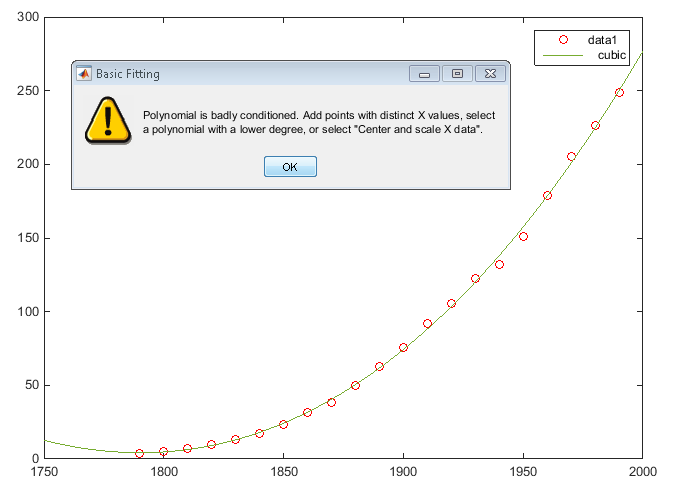
В вычислении соответствия MATLAB сталкивается с проблемами и выдает следующее предупреждение:
Polynomial is badly conditioned. Add points with distinct X values, select a polynomial with a lower degree, or select "Center and scale X data."
Это предупреждение указывает, что вычисленные коэффициенты для модели чувствительны к случайным ошибкам в ответе (измеренное население). Это также предлагает некоторые вещи, которые можно сделать, чтобы получить лучшее соответствие.
Продолжите использовать кубическое соответствие. Когда вы не можете добавить новые наблюдения к данным переписи, улучшить соответствие путем преобразования значений, вы имеете к z-очкам прежде, чем повторно вычислить соответствие. Выберите Center и масштабируйтесь, X проверок данных окружают диалоговое окно, чтобы заставить инструмент Basic Fitting выполнить преобразование.
Чтобы изучить, как центрирование и масштабирование данных работают, смотрите Узнать, как, что Основной Подходящий Инструмент Вычисляет Соответствия.
Представление Now уравнения и невязки отображения. В дополнение к выбору Center и шкалы X данных и кубические флажки, выберите следующие опции:
Покажите уравнения
Постройте график невязок
Покажите норму невязок
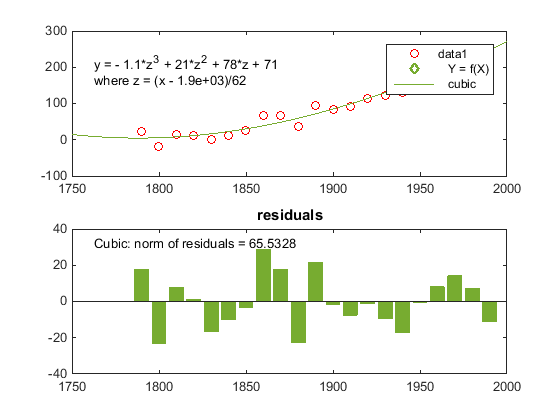
Выбор невязок Plot создает подграфик их как гистограмма. Следующая фигура отображает результаты опций Пользовательского интерфейса Basic Fitting, которые вы выбрали.
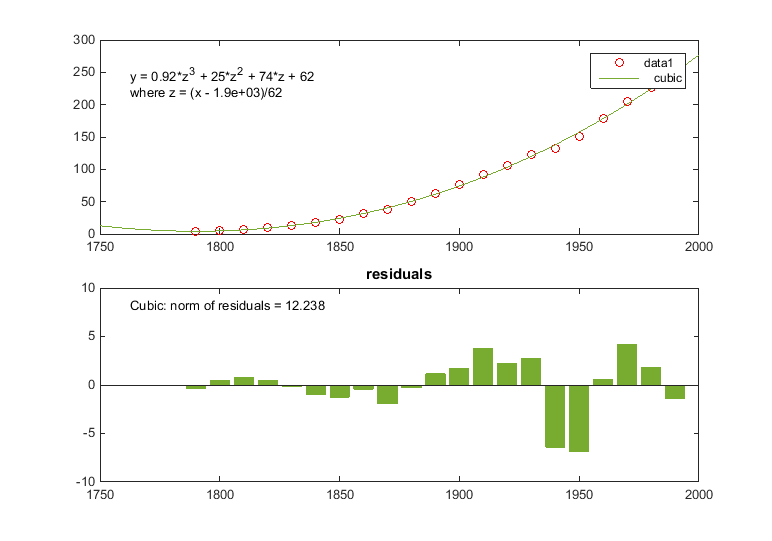
Кубическое соответствие является плохим предиктором перед годом 1790, где это указывает на уменьшающееся население. Модель, кажется, аппроксимирует данные обоснованно много позже 1790. Однако шаблон в невязках показывает, что модель не соответствует предположению о нормальной ошибке, которая является основанием для подбора кривой наименьших квадратов. Данные 1 строка, идентифицированная в легенде, являются наблюдаемым x (cdate) и y (pop) значения данных. Кубическая линия регрессии представляет соответствие после центрирования и масштабирования значений данных. Заметьте, что данные показывают исходные модули данных, даже при том, что инструмент вычисляет соответствие с помощью преобразованных z-очков.
Для сравнения попытайтесь соответствовать другому полиномиальному уравнению к данным переписи путем выбора его в области соответствий Графика.
В диалоговом окне Basic Fitting кликните по кнопке стрелки![]() , чтобы отобразить предполагаемые коэффициенты и норму невязок в Числовой панели результатов.
, чтобы отобразить предполагаемые коэффициенты и норму невязок в Числовой панели результатов.
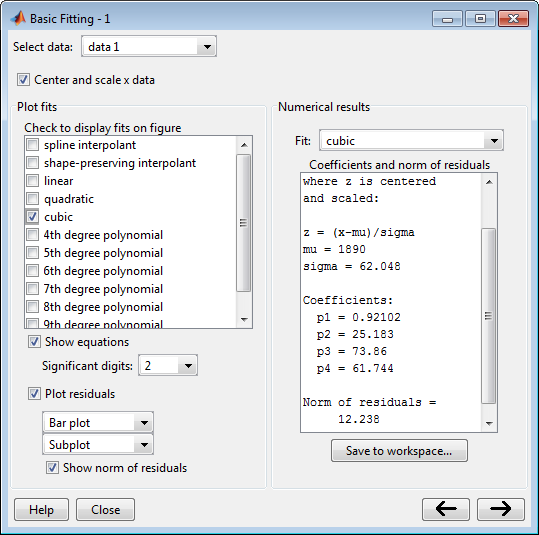
Чтобы просмотреть определенное соответствие, выберите его из Подходящего списка. Это отображает коэффициенты в диалоговом окне Basic Fitting, но не строит график соответствия в окне фигуры.
Если вы также хотите отобразить соответствие на графике, необходимо установить соответствующий флажок соответствий Графика.
Сохраните подходящие данные к MATLAB workspace путем нажатия на Save к кнопке рабочей области на Числовой панели результатов. Диалоговое окно Save Fit to Workspace открывается.
Со всеми установленными флажками нажмите ОК, чтобы сохранить подходящие параметры как структуру MATLAB:
fit
fit =
type: 'polynomial degree 3'
coeff: [0.9210 25.1834 73.8598 61.7444]
Теперь, можно использовать подходящие результаты в программировании MATLAB, за пределами Пользовательского интерфейса Basic Fitting.
Можно получить индикацию относительно того, как хорошо параболическая регрессия предсказывает наблюдаемые данные путем вычисления коэффициента определения или R-квадрата (записанный как R2). Статистическая величина R2, которая колеблется от 0 до 1, меры, насколько полезный независимая переменная находится в предсказании значений зависимой переменной:
Значение R2 около 0 указывает, что соответствие не намного лучше, чем образцовый y = constant.
Значение R2 около 1 указывает, что независимая переменная объясняет большую часть изменчивости в зависимой переменной.
Чтобы вычислить R2, сначала вычислите соответствие, и затем получите невязки из него. Невязка является различием со знаком между наблюдаемым зависимым значением и значением, которое ваше соответствие предсказывает для него.
невязки = yobserved - yfitted
После того, как у вас есть остаточные значения, можно сохранить их в рабочую область, где можно вычислить R2. Завершите предыдущую часть этого примера, чтобы соответствовать кубическому полиному к данным переписи, и затем выполнить эти шаги:
Вычислите остаточные данные и R2 для кубического соответствия
Кликните по кнопке стрелки![]() в нижнем правом углу, чтобы открыть Числовую вкладку результатов, если это не уже видимо.
в нижнем правом углу, чтобы открыть Числовую вкладку результатов, если это не уже видимо.
Из Подходящего выпадающего меню выберите cubic, если это уже не показывает.
Сохраните подходящие коэффициенты, норму невязок и невязок путем нажатия на Save to Workspace.
Диалоговое окно Save Fit to Workspace открывается тремя флажками и тремя текстовыми полями.
Установите все три флажка, чтобы сохранить подходящие коэффициенты, норму невязок и остаточные значения.
Идентифицируйте сохраненные переменные как принадлежащий кубическому соответствию. Измените имена переменных путем добавления 3 к каждому имени по умолчанию (например, fit3, normresid3 и resids3). Диалоговое окно должно выглядеть так фигура.
Нажать ОК. Основной Подбор кривой сохраняет невязки как вектор - столбец чисел, подходящие коэффициенты как struct и норма невязок как скаляр.
Заметьте, что значением, которое Основной Подбор кривой вычисляет для нормы невязок, является 12.2380. Этот номер является квадратным корнем из суммы квадратов остатков кубического соответствия.
Опционально, можно проверить значение нормы невязок что обеспеченный инструмент Basic Fitting. Вычислите норму невязок сами из массива resids3, который вы просто сохранили:
mynormresid3 = sum(resids3.^2)^(1/2)
mynormresid3 =
12.2380Вычислите полную сумму квадратов зависимой переменной, pop, чтобы вычислить R2. Полная сумма квадратов является суммой различий в квадрате каждого значения от среднего значения переменной. Например, используйте этот код:
SSpop = (length(pop)-1) * var(pop)
SSpop =
1.2356e+005
var(pop) вычисляет отклонение вектора населения. Вы умножаете его на количество наблюдений после вычитания 1, чтобы составлять степени свободы. И полная сумма квадратов и норма невязок являются положительными скалярами. Теперь, вычислите R2, с помощью квадрата normresid3 и SSpop:
rsqcubic = 1 - normresid3^2 / SSpop
rsqcubic =
0.9988
Наконец, вычислите R2 для линейного соответствия и сравните его с кубическим значением R2, которое вы просто получили. Пользовательский интерфейс Basic Fitting также предоставляет вам линейные подходящие результаты. Чтобы получить линейные результаты, повторите шаги 2-6, изменив ваши действия можно следующим образом:
Чтобы вычислить наименьшие квадраты, линейные коэффициенты регрессии и статистика, в Соответствии, выпадающем на Числовой панели результатов, выбирают linear instead of cubic.
В Сохранении в диалоговое окно Рабочей области добавьте 1 к каждому имени переменной, чтобы идентифицировать его как выводящий от линейного соответствия и нажать ОК. Переменные fit1, normresid1 и resids1 теперь существуют в рабочей области.
Используйте переменный normresid1 (98.778), чтобы вычислить R2 для линейного соответствия, как вы сделали на шаге 9 для кубического соответствия:
rsqlinear = 1 - normresid1^2 / SSpop
rsqlinear =
0.9210
Этот результат указывает, что линейный припадок наименьших квадратов данных о населении объясняет 92,1% своего отклонения. Как кубический припадок этого данные объясняют 99,9% того отклонения, последний, кажется, лучший предиктор. Однако, потому что кубическое соответствие предсказывает использование трех переменных (x, x2, и x3), основное значение R2 не полностью отражает, насколько устойчивый соответствие. Более соответствующая мера для оценки совершенства многомерных соответствий настроена R2. Для получения информации о вычислении и использовании настроенный R2, смотрите Невязки и Совершенство Соответствия.
R2 измеряется, как хорошо ваше полиномиальное уравнение предсказывает зависимую переменную, насколько соответствующий полиномиальная модель для ваших данных. Когда вы анализируете по сути непредсказуемые данные, маленькое значение R2 указывает, что независимая переменная не предсказывает зависимой переменной точно. Однако это не обязательно означает, что существует что-то не так с соответствием.
Вычислите Остаточные Данные и R2 для Линейного Соответствия. В этом следующем примере используйте Пользовательский интерфейс Basic Fitting, чтобы выполнить линейное соответствие, сохранить результаты в рабочую область и вычислить R2 для линейного соответствия. Можно затем сравнить линейный R2 с кубическим значением R2, которое вы получаете в примере, Вычисляют Остаточные Данные и R2 для Кубического Соответствия.
Кликните по кнопке стрелки![]() в нижнем правом углу, чтобы открыть Числовую вкладку результатов, если это не уже видимо.
в нижнем правом углу, чтобы открыть Числовую вкладку результатов, если это не уже видимо.
Установите линейный флажок в области соответствий Графика.
Из Подходящего выпадающего меню выберите linear, если это уже не показывает. Коэффициенты и норма области невязок отображают статистику для линейного соответствия.
Сохраните подходящие коэффициенты, норму невязок и невязок путем нажатия на Save to Workspace.
Диалоговое окно Save Fit to Workspace открывается тремя флажками и тремя текстовыми полями.
Установите все три флажка, чтобы сохранить подходящие коэффициенты, норму невязок и остаточные значения.
Идентифицируйте сохраненные переменные как принадлежащий линейному соответствию. Измените имена переменных путем добавления 1 к каждому имени по умолчанию (например, fit1, normresid1 и resids1).
Нажать ОК. Основной Подбор кривой сохраняет невязки как вектор - столбец чисел, подходящие коэффициенты как struct и норма невязок как скаляр.
Заметьте, что значением, которое Основной Подбор кривой вычисляет для нормы невязок, является 98.778. Этот номер является квадратным корнем из суммы квадратов остатков линейного соответствия.
Опционально, можно проверить значение нормы невязок что обеспеченный инструмент Basic Fitting. Вычислите норму невязок сами из массива resids1, который вы просто сохранили:
mynormresid1 = sum(resids1.^2)^(1/2)
mynormresid1 =
98.7783Вычислите полную сумму квадратов зависимой переменной, pop, чтобы вычислить R2. Полная сумма квадратов является суммой различий в квадрате каждого значения от среднего значения переменной. Например, используйте этот код:
SSpop = (length(pop)-1) * var(pop)
SSpop =
1.2356e+005
var(pop) вычисляет отклонение вектора населения. Вы умножаете его на количество наблюдений после вычитания 1, чтобы составлять степени свободы. И полная сумма квадратов и норма невязок являются положительными скалярами. Теперь, вычислите R2, с помощью квадрата normresid1 и SSpop:
rsqlinear = 1 - normresid1^2 / SSpop
rsqcubic =
0.9210
Этот результат указывает, что линейный припадок наименьших квадратов данных о населении объясняет 92,1% своего отклонения. Как кубический припадок этого данные объясняют 99,9% того отклонения, последний, кажется, лучший предиктор. Однако кубическое соответствие имеет четыре коэффициента (x, x2, x3, и константа), в то время как линейное соответствие имеет два коэффициента (x и константа). Простая статистическая величина R2 не составляет различные степени свободы. Более соответствующая мера для оценки аппроксимаций полиномом настроена R2. Для получения информации о вычислении и использовании настроенный R2, смотрите Невязки и Совершенство Соответствия.
R2 измеряется, как хорошо ваше полиномиальное уравнение предсказывает зависимую переменную, насколько соответствующий полиномиальная модель для ваших данных. Когда вы анализируете по сути непредсказуемые данные, маленькое значение R2 указывает, что независимая переменная не предсказывает зависимой переменной точно. Однако это не обязательно означает, что существует что-то не так с соответствием.
Предположим, что вы хотите использовать кубическую модель, чтобы интерполировать население U.S. в 1 965 (дата, не обеспеченная в исходных данных).
В диалоговом окне Basic Fitting нажмите![]() кнопку, чтобы задать вектор значений
кнопку, чтобы задать вектор значений x, в которых можно оценить текущее соответствие.
Во Ввести значении (значениях)... поле, введите следующее значение:
1965
Используйте немасштабированные и значения x нев центре. Вы не должны центрироваться и масштабироваться сначала, даже при том, что вы выбрали, чтобы масштабироваться, значения x, чтобы получить коэффициенты в Предсказывают Данные переписи с Соответствием Кубического полинома. Инструмент Basic Fitting вносит необходимые корректировки негласно.
Нажмите Evaluate.
Значения x и соответствующие значения для f(x), вычисленного из соответствия и отображенного в таблице, как показано ниже:
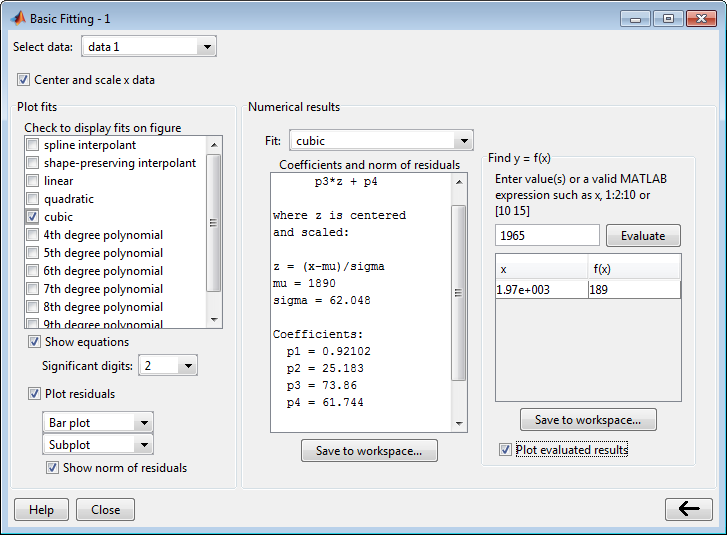
Установите оцененный флажок результатов Plot, чтобы отобразить интерполированное значение как ромбовидный маркер:
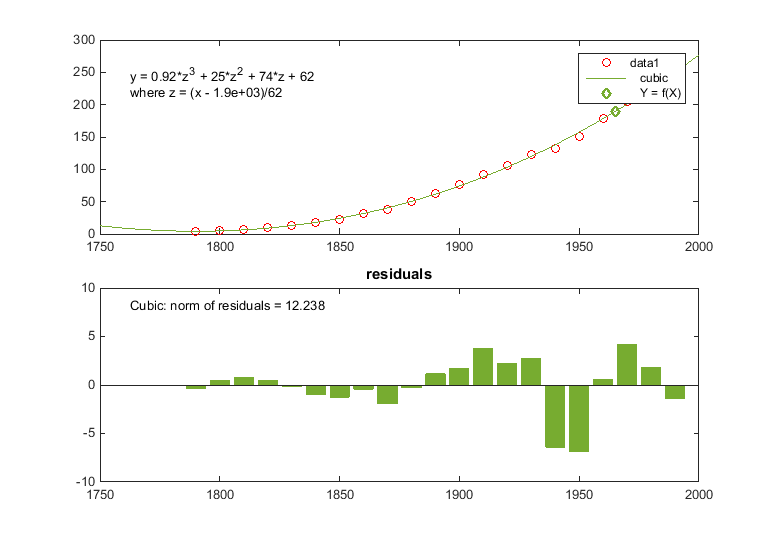
Сохраните интерполированное население в 1 965 к MATLAB workspace путем нажатия на Save к рабочей области.
Это открывает следующее диалоговое окно, где вы задаете имена переменных:
Нажмите ОК, но сохраните Окно фигуры открытым, если вы намереваетесь выполнить шаги в следующем разделе, Сгенерируйте Файл кода, чтобы Воспроизвести Результат.
После завершения Основного Подходящего сеанса можно сгенерировать код MATLAB, который повторно вычисляет соответствия и воспроизводит графики с новыми данными.
В Окне фигуры выберите File> Generate Code.
Это создает функцию и отображает ее в редакторе MATLAB. Код показывает вам, как программно воспроизвести то, что вы сделали в интерактивном режиме с диалоговым окном Basic Fitting.
Измените имя функции на первой строке от createfigure до чего-то более определенного, как censusplot. Сохраните файл кода в свою текущую папку с именем файла censusplot.m, с которого начинается функция:
function censusplot(X1, Y1, valuesToEvaluate1)
Сгенерируйте немного новые, случайным образом встревоженные данные переписи:
randpop = pop + 10*randn(size(pop));
Воспроизведите график с новыми данными и повторно вычислите соответствие:
censusplot(cdate,randpop,1965)
Вам нужны три входных параметра: x, y значения (data 1), построенный график в исходном графике, плюс x-значение для маркера.
Следующая фигура отображает график, который производит сгенерированный код. Новый график совпадает с внешним видом фигуры от который вы сгенерированный код за исключением y значений данных, уравнения для кубического соответствия и остаточных значений в гистограмме, как ожидалось.
Инструмент Basic Fitting вызывает функцию polyfit, чтобы вычислить аппроксимации полиномом. Это вызывает функцию polyval, чтобы оценить соответствия. polyfit анализирует свои входные параметры, чтобы определить, подготовлены ли данные хорошо для требуемого градуса соответствия.
Когда это находит плохо подготовленные данные, polyfit вычисляет регрессию, а также это может, но это также возвращает предупреждение, что соответствие могло быть улучшено. Основной Подходящий раздел Predict the Census Data в качестве примера с Соответствием Кубического полинома отображает это предупреждение.
Один способ улучшить надежность модели состоит в том, чтобы добавить точки данных. Однако добавление наблюдений к набору данных не всегда выполнимо. Альтернативная стратегия состоит в том, чтобы преобразовать переменную прогноза, чтобы нормализовать ее центр и шкалу. (В примере предиктор является вектором дат переписи.)
Функция polyfit нормализует вычислительными z-очками:
где x является данными предиктора, μ является средним значением x, и σ является стандартным отклонением x. Z-очки дают данным среднее значение 0 и стандартное отклонение 1. В Пользовательском интерфейсе Basic Fitting вы преобразовываете данные предиктора к z-очкам путем выбора Center и масштабируете x поле проверки данных.
После центрирования и масштабирования, образцовые коэффициенты вычисляются для y данных как функция z. Они отличаются (и более устойчивы), чем коэффициенты, вычисленные для y как функция x. Форма модели и норма невязок не изменяются. Пользовательский интерфейс Basic Fitting автоматически повторно масштабирует z-очки так, чтобы соответствие построило график в той же шкале как исходные x данные.
Чтобы понять путь, которым и масштабированные данные в центре используется в качестве посредника, чтобы создать итоговый график, запустите следующий код в Командном окне:
close load census x = cdate; y = pop; z = (x-mean(x))/std(x); % Compute z-scores of x data plot(x,y,'ro') % Plot data as red markers hold on % Prepare axes to accept new graph on top zfit = linspace(z(1),z(end),100); pz = polyfit(z,y,3); % Compute conditioned fit yfit = polyval(pz,zfit); xfit = linspace(x(1),x(end),100); plot(xfit,yfit,'b-') % Plot conditioned fit vs. x data
И масштабированный кубический полином в центре строит график как синяя строка, как показано здесь:
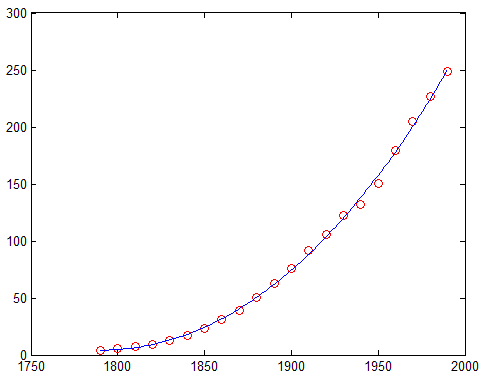
В коде вычисление z иллюстрирует, как нормализовать данные. Функция polyfit выполняет само преобразование, если вы обеспечиваете три возвращаемых аргумента при вызове его:
[p,S,mu] = polyfit(x,y,n)
p, теперь основаны, нормализовал x. Возвращенный вектор, mu, содержит среднее и стандартное отклонение x. Для получения дополнительной информации смотрите страницу с описанием polyfit.