Геоцентрический к геодезической широте

Преобразуйте геоцентрическую широту в геодезическую широту

Библиотека

Преобразования утилит/Осей

Описание

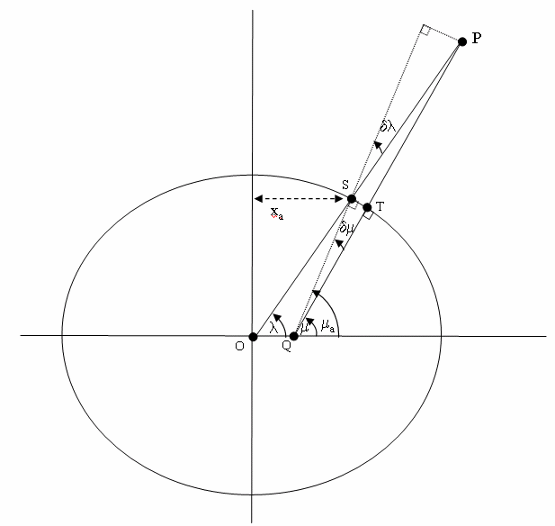
Блок Geocentric to Geodetic Latitude преобразовывает геоцентрическую широту (λ) в геодезическую широту (μ). Существует много геометрических отношений, которые используются, чтобы вычислить геодезическую широту в этом неитеративном методе. Много углов и точек вовлечены в вычисление, которые показывают в следующей фигуре.

Учитывая геоцентрическую широту (λ) и радиус (r) от центра планеты (O) к центру тяжести (P), этот неитеративный метод запускается вычислительными значениями для точки r, который прерывает поверхность планеты (S). Путем реорганизации уравнения для эллипса, горизонтальной координаты, $(x_{a})$ определяется. Когда экваториальный радиус (R), полярный радиус $((1 - f) R)$ и $x_{a} загар λ$ , заменены полуглавную ось, полунезначительную ось и вертикальную координату $(y_{a})$ , получившееся уравнение для $x_{a}$ имеет следующую форму:

$x_{a} = \frac{(1 - f) R}{\sqrt{{загар}^{2} λ + {(1 - f)}^{2}}}$

Определить геодезическую широту в S $μ_{a}$ , уравнение для эллипса с экваториальным радиусом (R), полярный радиус $((1 - f) R)$ используется снова. На этот раз это используется, чтобы задать $y_{a}$ с точки зрения $x_{a}$ .

$y_{a} = \sqrt{R^{2} - x_{a}^{2}} (1 - f)$

Кроме того, отношение между геоцентрической широтой в поверхностной и геодезической широте планеты используется.

$μ_{a} = atan (\frac{загар λ}{{(1 - f)}^{2}})$

Используя отношение $загар λ = y_{a} / x_{a}$ и эти два уравнения выше, получившееся уравнение для $μ_{a}$ получен.

$μ_{a} = atan (\frac{\sqrt{R^{2} - x_{a}^{2}}}{(1 - f) x_{a}})$

Правильный знак $μ_{a}$ определяется путем тестирования λ и если λ является меньше, чем нуль $μ_{a}$ изменяет знак соответственно.

В порядке вычислить геодезическую широту P, много геометрических отношений требуются, чтобы быть вычисленными. Эти вычисления следуют.

Радиус $(r_{a})$ от центра планеты (O) на поверхность планеты (S) вычисляется при помощи тригонометрического отношения.

$r_{a} = \frac{x_{a}}{потому что λ}$

Расстояние от S до P задано:

$l = r - r_{a}$

Угловое различие между геоцентрической широтой и геодезической широтой в S (δλ) задано:

$δ λ = μ_{a} - λ$

Используя $l$ и δλ, сегмент TP или высота среднего уровня моря (h) оцениваются.

$h = l потому что δ λ$

Уравнение для радиуса искривления в Меридиане $(ρ_{a})$ в $μ_{a}$

$ρ_{a} = \frac{R {(1 - f)}^{2}}{{(1 - (2 f - f^{2}) \sin^{2} μ_{a})}^{3 / 2}}$

Используя $l$ , δλ, h, и $ρ_{a}$ , угловое различие между геодезической широтой в S $(μ)$ и геодезическая широта в P $(μ_{a})$ задан как:

$δ μ = atan (\frac{l \sin δ λ}{ρ_{a} + h})$

Вычитание δμ от $μ_{a}$ затем дает μ.

$μ = μ_{a} - δ μ$

Параметры

Units

Задает параметр и устройства вывода:

Модули	Радиус от CG до центра планеты	Экваториальный радиус
`Metric (MKS)`	Метры	Метры
`English`	Футы	Футы

Эта опция только доступна, когда модель Planet установлена в Earth (WGS84).

Planet model

Задает модель планеты, чтобы использовать: Custom или Earth (WGS84).

Flattening

Задает выравнивание планеты. Эта опция только доступна с набором модели Planet Custom.

Equatorial radius of planet: Задает радиус планеты в ее экваторе. Модули экваториального параметра радиуса должны совпасть с модулями для радиуса. Эта опция только доступна с набором модели Planet Custom.

Вводы и выводы

Входной параметр	Тип размерности	Описание
Сначала	Скаляр	Содержит геоцентрическую широту, в градусах. Значения широты могут быть любым значением. Однако значения +90 и-90 могут возвратить неожиданные значения из-за особенности в полюсах.
Второй	Скаляр	Содержит радиус от центра планеты к центру тяжести.

Вывод	Тип размерности	Описание
Сначала	Скаляр	Содержит геодезическую широту, в градусах.

Предположения и ограничения

Эта реализация генерирует геодезическую широту, которая находится между ±90 градусами.

Ссылки

Джексон, E. B. руководство для основанной на рабочей станции типичной программы симуляции рейса (LaRCsim) версия 1.4, NASA TM 110164, апрель 1995.

Hedgley, D. R. младший, “Точное преобразование от геоцентрического до геодезических координат для ненулевых высот”, TR НАСА R-458, март 1976.

Clynch, J. R. “Радиус земли - радиусы, используемые в геодезии”, Высшая школа ВМС США, 2002, http://www.oc.nps.edu/oc2902w/geodesy/radiigeo.pdf.

Стивенс, B. L., и Ф. Л. Льюис, управление самолетом и Simulation, John Wiley & Sons, Нью-Йорк, 1992.

Эдвардс, C. H., и Д. Э. Пенни, исчисление и аналитическая геометрия 2-й выпуск, Prentice Hall, Englewood Cliffs, Нью-Джерси, 1986.

Смотрите также

Положение ECEF к LLA

Плоская земля к LLA

Геодезический к геоцентрической широте

LLA к позиции ECEF

Документация