distspec
Вычислите спектр расстояния сверточного кода
Синтаксис
spect = distspec(trellis,n)
spect = distspec(trellis)
Описание
spect = distspec(trellis,n) вычисляет свободное расстояние и первые компоненты n веса и спектры расстояния линейного сверточного кода. Поскольку сверточные коды не имеют контуров блока, спектр веса и спектр расстояния полубесконечны и чаще всего аппроксимируются первыми несколькими компонентами. Вход trellis является допустимой структурой решетки MATLAB, как описано в Описании Решетки Сверточного кода. Вывод, spect, является структурой с этими полями:
| Поле | Значение |
|---|---|
spect.dfree | Свободное расстояние кода. Это - минимальное количество ошибок в закодированной последовательности, требуемой создать ошибочное событие. |
spect.weight | Вектор длины-n, который перечисляет общее количество информационных битовых ошибок в ошибочных событиях, перечисленных в spect.event. |
spect.event | Вектор длины-n, который перечисляет количество ошибочных событий для каждого расстояния между spect.dfree и spect.dfree+n-1. Вектор представляет первые компоненты n спектра расстояния. |
spect = distspec(trellis) совпадает с spect = distspec(trellis,1).
Примеры
Пример ниже выполняет эти задачи:
Вычисляет спектр расстояния для уровня 2/3 сверточный код, который изображен на странице с описанием для функции
poly2trellisИспользует вывод
distspecкак вход к функцииbercoding, чтобы найти теоретическую верхнюю границу на частоте ошибок по битам для системы, которая использует этот код с когерентной модуляцией BPSKСтроит верхнюю границу с помощью функции
berfit
trellis = poly2trellis([5 4],[23 35 0; 0 5 13]) spect = distspec(trellis,4) berub = bercoding(1:10,'conv','hard',2/3,spect); % BER bound berfit(1:10,berub); ylabel('Upper Bound on BER'); % Plot.
Вывод и график ниже.
trellis =
numInputSymbols: 4
numOutputSymbols: 8
numStates: 128
nextStates: [128x4 double]
outputs: [128x4 double]
spect =
dfree: 5
weight: [1 6 28 142]
event: [1 2 8 25]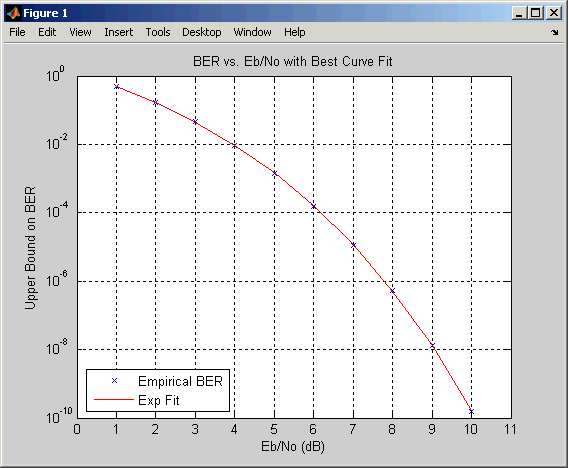
Алгоритмы
Функция использует алгоритм поиска по дереву, реализованный со стеком, как описано в [2].
Ссылки
[1] Бочарова, Т.е. и Б. Д. Кудряшов, “Рациональный Уровень Проколотые Сверточные коды для Декодирования Soft-Decision Viterbi”, Транзакции IEEE на Теории информации, Издании 43, № 4, июль 1997, стр 1305–1313.
[2] Cedervall, M. и Р. Йоханнессон, “Алгоритм FAST для Вычислительного Спектра Расстояния Сверточных кодов”, Транзакции IEEE на Теории информации, Издании 35, № 6, ноябрь 1989, стр 1146–1159.
[3] Чанг, J., Д. Хван и М. Лин, “Некоторые Расширенные Результаты на поиске хороших Сверточных кодов”, Транзакции IEEE на Теории информации, Издании 43, № 5, сентябрь 1997, стр 1682–1697.
[4] Frenger, P., П. Ортен и Т. Оттоссон, “Комментарии и Добавления к Недавним Статьям о Новых Сверточных кодах”, Транзакции IEEE на Теории информации, Издании 47, № 3, март 2001, стр 1199–1201.