Кодирование контроля циклическим избыточным кодом (CRC) является методом кодирования контроля ошибок для обнаружения ошибок, которые происходят, когда сообщение передается. В отличие от блочных или сверточных кодов, коды CRC не имеют встроенной возможности исправления ошибок. Вместо этого когда система связи обнаруживает ошибку в полученном слове сообщения, получатель запрашивает отправителя ретранслировать слово сообщения.
В кодировании CRC передатчик применяет правило к каждому слову сообщения, чтобы создать дополнительные биты, названные контрольной суммой или синдромом, и затем добавляет контрольную сумму к слову сообщения. После получения переданного слова получатель применяет то же правило к полученному слову. Если получившаяся контрольная сумма является ненулевой, ошибка произошла, и передатчик должен снова послать слово сообщения.
Откройте библиотеку Error Detection и Correction путем двойного клика по ее значку в основной библиотеке блоков Communications Toolbox™. Откройте подбиблиотеку CRC путем двойного клика на ее значке в библиотеке Error Detection и Correction.
Communications Toolbox поддерживает Кодирование CRC с помощью блоков Simulink®, Системных объектов или объектов MATLAB®.
Для списка стандартных программ кодирования CRC поддержки Communications Toolbox видят, что Контроль циклическим избыточным кодом Кодирует.
CRC непрямой алгоритм принимает вектор двоичных данных, соответствуя полиному M, и добавляет контрольную сумму r битов, соответствуя полиному C. Конкатенация входного вектора и контрольной суммы затем соответствует полиномиальному T = M * xr +, C, начиная с умножения на xr соответствует сдвигу входного вектора биты r налево. Алгоритм выбирает контрольную сумму C так, чтобы T был делимым предопределенным полиномиальным P степени r, названный полиномом генератора.
Алгоритм делит T на P и устанавливает контрольную сумму, равную бинарному вектору, соответствующему остатку. Таким образом, если T = Q * P + R, где R является полиномом степени меньше, чем r, контрольная сумма, является бинарным вектором, соответствующим R. При необходимости алгоритм предварительно ожидает нули к контрольной сумме так, чтобы это имело длину r.
Функция генерации CRC, которая реализует фазу передачи алгоритма CRC, делает следующее:
Сдвиги влево вектор входных данных битами r и делят соответствующий полином на P.
Устанавливает контрольную сумму, равную бинарному вектору длины r, соответствуя остатку от шага 1.
Добавляет контрольную сумму к вектору входных данных. Результатом является выходной вектор.
Функция обнаружения CRC вычисляет контрольную сумму для своего целого входного вектора, как описано выше.
Алгоритм CRC использует бинарные векторы, чтобы представлять бинарные полиномы, в порядке убывания степеней. Например, векторный [1 1 0 1] представляет полином x3 + x2 + 1.
Реализация, описанная в этом разделе, является одной из многих допустимых реализаций алгоритма CRC. Различные реализации могут привести к различным числовым результатам.
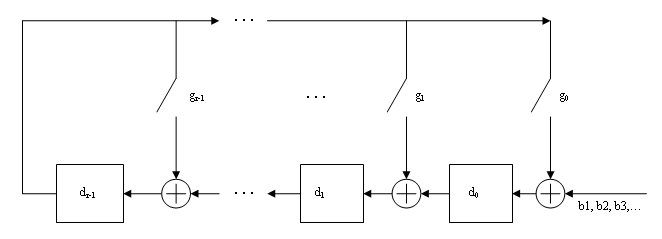
Биты вводят линейный сдвиговый регистр обратной связи (LFSR) от самого низкого индексного бита до самого высокого индексного бита. Последовательность битов входного сигнала представляет коэффициенты полинома сообщения в порядке уменьшающихся степеней. Вектор сообщения увеличивается с нулями r, чтобы спугнуть LFSR, где r является степенью полинома генератора. Если вывод от крайнего левого этапа d (1) регистра является 1, то биты в сдвиговом регистре являются XORed с коэффициентами полинома генератора. Когда увеличенная последовательность сообщения полностью отправляется через LFSR, регистр содержит контрольную сумму [d (1) d (2)... d (r)]. Это - реализация бинарного длинного деления, в котором последовательность сообщения является делителем (числитель), и полином является дивидендом (знаменатель). Контрольная сумма CRC является остатком от операции деления.
Предположим, что входным кадром является [1 1 0 0 1 1 0]', соответствуя полиному M = x6 +x 5 + x2 + x, и полином генератора является P = x3 + x2 + 1 степени r = 3. Полиномиальным делением, M*x3 = (x6 + x3 + x) * P + x. Остаток является R = x, так, чтобы контрольной суммой был затем [0 1 0]'. Дополнительный 0 добавляется слева, чтобы заставить контрольную сумму иметь длину 3.
где
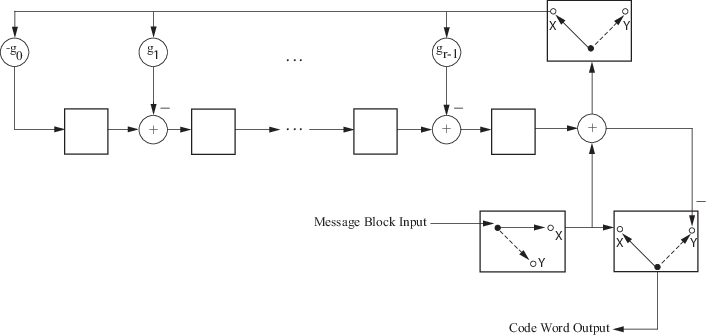
Обменивайтесь сообщениями Вход Блока
Кодовая комбинация Вывод
Начальный шаг прямого кодирования CRC происходит с тремя переключателями в положении X. Алгоритм кормит битами сообщения k энкодер. Эти биты являются первыми битами k кодовой комбинации вывод. Одновременно, алгоритм отправляет биты k в линейный сдвиговый регистр обратной связи (LFSR). Когда система полностью питается, k th передают бит к LFSR, переключатели перемещаются в положение Y. Здесь, LFSR содержит математический остаток от полиномиального деления. Эти биты переключены из LFSR, и они - остающиеся биты (контрольная сумма) кодовой комбинации вывод.
[1] Sklar, Бернард., цифровая связь: основные принципы и приложения, Englewood Cliffs, NJ, Prentice Hall, 1988.
[2] Ивовый прут, Стивен Б., системы контроля ошибок для цифровой связи и устройства хранения данных, верхнего Сэддл-Ривер, NJ, Prentice Hall, 1995.
Методы кодирования контроля ошибок обнаруживают, и возможно исправляют, ошибки, которые происходят, когда сообщения передаются в системе цифровой связи. Чтобы выполнить это, энкодер передает не только информационные символы, но также и дополнительные избыточные символы. Декодер интерпретирует то, что он получает, с помощью избыточных символов, чтобы обнаружить и возможно исправить независимо от того, что ошибки произошли во время передачи. Вы можете использовать кодирование контроля ошибок, если ваш канал передачи является очень шумным или если ваши данные очень чувствительны к шуму. В зависимости от природы данных или шума, вы можете выбрать определенный тип кодирования контроля ошибок.
Блочное кодирование является особым случаем кодирования контроля ошибок. Методы блочного кодирования сопоставляют постоянное число символов сообщения к постоянному числу кодовых знаков. Кодер блока обрабатывает каждый блок данных независимо и является устройством без памяти. Communications Toolbox содержит возможности блочного кодирования путем обеспечения блоков Simulink, Системных объектов и функций MATLAB.
Класс методов блочного кодирования включает категории, показанные в схему ниже.
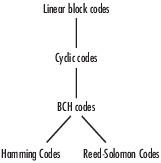
Communications Toolbox поддерживает общие линейные блочные коды. Это также обрабатывает циклический, BCH, Хэмминг и коды Тростника-Solomon (которые являются всеми специальными видами линейных блочных кодов). Блоки в продукте могут закодировать или декодировать сообщение с помощью одного из ранее упомянутых методов. Тростник-Solomon и декодеры BCH указывают, сколько ошибок они обнаружили при декодировании. Кодеры Тростника-Solomon также позволяют вам решить, использовать ли символы или биты как ваши данные.
Блоки и функции в Communications Toolbox разработаны для кодов контроля ошибок, которые используют алфавит, имеющий символы на 2 или 2 м.
Функции поддержки Communications Toolbox. Функции в Communications Toolbox могут поддержать блоки симуляции
Определяя характеристики метода, такие как возможность исправления ошибок или возможные длины сообщения
Выполняя вычисления низшего уровня, сопоставленные с методом, такой как
Вычисление таблицы истинности
Вычисление генератора или матрицы проверки четности
Преобразование между генератором и матрицами проверки четности
Вычисление полинома генератора
Для получения дополнительной информации о возможностях кодирования контроля ошибок, смотрите Блочные коды.
В этом разделе информация, которая будет закодирована, состоит из символов сообщения и кода, который производится, состоит из кодовых комбинаций.
Каждый блок символов сообщения K закодирован в кодовую комбинацию, которая состоит из символов сообщения N. K называется длиной сообщения, N называется длиной кодовой комбинации, и код называется [N, K] код.
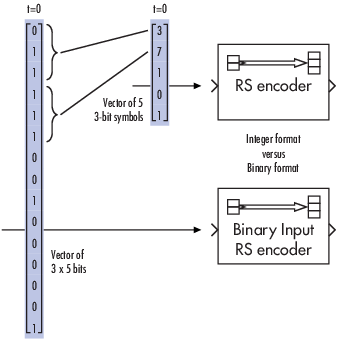
Каждое сообщение или кодовая комбинация являются упорядоченной группировкой символов. Каждый блок в подбиблиотеке Block Coding обрабатывает одно слово в каждом временном шаге, как описано в следующем разделе, Двоичный формат (Все Методы Кодирования). Кодеры тростника-Solomon также позволяют вам выбрать между двоичными и целочисленными данными, как описано в Целочисленном формате (Только Тростник-Solomon).
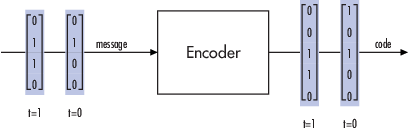
Двоичный формат (Все Методы Кодирования). Можно структурировать сообщения и кодовые комбинации, когда бинарный вектор сигнализирует, где каждый вектор представляет слово сообщения или кодовую комбинацию. В установленный срок энкодер получает целое слово сообщения, кодирует его и выводит целую кодовую комбинацию. Сигналы сообщения и кода действуют по тому же шагу расчета.
Этот пример иллюстрирует энкодер, получающий четырехбитное сообщение и производящий пятибитную кодовую комбинацию во время 0. Это повторяет этот процесс с новым сообщением во время 1.
Для всех методов кодирования кроме Тростника-Solomon с помощью двоичного входа вектор сообщения должен иметь длину K, и соответствующий вектор кода имеет длину N. Для кодов Тростника-Solomon с двоичным входом символы для кода являются двоичными последовательностями длины M, соответствуя элементам GF Поля Галуа (2M). В этом случае вектор сообщения должен иметь длину, M*K и соответствующий вектор кода имеют длину M*N. Блок Binary-Input RS Encoder и блок Binary-Output RS Decoder используют этот формат для сообщений и кодовых комбинаций.
Если вход к блоку блочного кодирования является основанным на кадре вектором, это должен быть вектор-столбец вместо вектора - строки.
Чтобы произвести основанные на выборке сообщения в двоичном формате, можно сконфигурировать блок Bernoulli Binary Generator так, чтобы его параметр Probability of a zero был вектором, длина которого является длиной сигнала, который вы хотите создать. Чтобы произвести основанные на кадре сообщения в двоичном формате, можно сконфигурировать тот же блок так, чтобы его параметр Probability of a zero был скаляром, и его параметр Samples per frame является длиной сигнала, который вы хотите создать.
Используя последовательные сигналы
Если вы предпочитаете структурировать сообщения и кодовые комбинации, когда скаляр сигнализирует, где несколько выборок совместно формируют слово сообщения или кодовую комбинацию, можно использовать Буфер и Освободить буфер блоки. Буферизация включает задержку и многоскоростную обработку. Если ваша модель вычисляет коэффициенты ошибок, начальная задержка буферизующей кодирование комбинации влияет на параметр Receive delay в блоке Error Rate Calculation. Если вы не уверены в шагах расчета сигналов в вашей модели, кликните по меню Display и выберите Sample Time> Colors. Также можно присоединить Тестовые блоки к строкам коннектора, чтобы помочь оценить демонстрационную синхронизацию, буферизовав и задержки.
Целочисленный формат (Только Тростник-Solomon). Слово сообщения для [N, K] код Тростника-Solomon состоит из битов M*K, которые можно интерпретировать как K символы от 0 до 2M. Символы являются двоичными последовательностями длины M, соответствуя элементам GF Поля Галуа (2M), в порядке убывания степеней. Целочисленный формат для кодов Тростника-Solomon позволяет вам сообщения структуры и кодовые комбинации, когда целое число сигнализирует вместо двоичных сигналов. (Вход должен быть основанным на кадре вектор-столбцом.)
В этом контексте Simulink ожидает, что первый бит будет старшим значащим битом в символе. “Сначала” означает самый маленький индекс в векторе или самое маленькое время для серии скаляров.
Следующая фигура иллюстрирует эквивалентность между бинарными и целочисленными сигналами для энкодера Тростника-Solomon. Случай для декодера подобен.
Чтобы произвести основанные на выборке сообщения в целочисленном формате, можно сконфигурировать блок Random Integer Generator так, чтобы M-ary number и параметры Initial seed были векторами желаемой длины, и все записи вектора M-ary number 2M. Чтобы произвести основанные на кадре сообщения в целочисленном формате, можно сконфигурировать тот же блок так, чтобы его M-ary number и параметры Initial seed были скалярами, и его параметр Samples per frame является длиной сигнала, который вы хотите создать.
Если вы сконфигурировали кодеры, несколько советов могут помочь вам разместить их правильно в вашей модели:
Если блок имеет несколько выходных параметров, первый всегда является потоком кодирования данных.
Тростник-Solomon и блоки BCH имеют ошибочный счетчик как второй вывод.
Убедитесь, что размеры сигнала подходят для параметров маски. Например, если вы используете блок Binary Cyclic Encoder и устанавливаете Message length K на 4, входной сигнал должен быть вектором длины 4.
Если вы не уверены в размере сигналов в вашей модели, отмечание меню Display выбирает Signals and Ports > Signal Dimension.
Пример: Код тростника-Solomon в Целочисленном формате. Этот пример использует код Тростника-Solomon в целочисленном формате. Это иллюстрирует соответствующие длины вектора сигналов кода и сообщения для кодеров. Это также показывает исправление ошибок, с помощью простого способа ввести ошибки в каждую кодовую комбинацию.
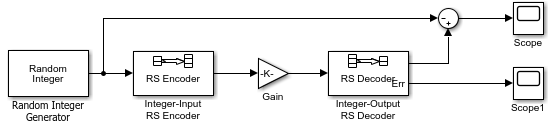
Откройте модель путем ввода doc_rscoding в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:
Случайный Целочисленный Генератор, в библиотеке Comm Sources
Установите M-ary number на 15.
Установите Initial seed на положительное число, randn выбран здесь.
Проверяйте флажок Frame-based outputs .
Установите Samples per frame на 5.
Введенный целым числом энкодер RS
Установите Codeword length N на 15.
Установите Message length K на 5.
Получите в библиотеке Simulink Math Operations
Установите Gain на [0; 0; 0; 0; 0; ones(10,1)].
Выведенный целым числом декодер RS
Установите Codeword length N на 15.
Установите Message length K на 5.
Определите объем в библиотеке Simulink Sinks. Получите две копии этого блока.
Суммируйте в библиотеке Simulink Math Operations
Установите List of signs на |-+
Соедините блоки как в предыдущей фигуре. Из меню Simulation окна модели выберите Model Configuration Parameters. В диалоговом окне Configuration Parameters, набор Stop Time к 500.
Числа длины вектора появляются на соединительных линиях, только если вы кликаете по меню Display и выбираете Signals & Ports> Signal Dimensions. Энкодер принимает вектор длины 5 (который является K в этом случае), и производит вектор длины 15 (который является N в этом случае). Декодер делает противоположное.
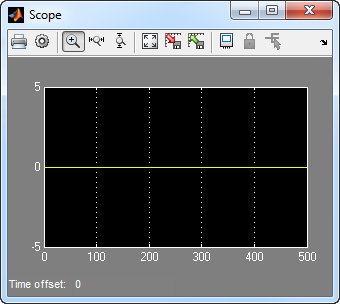
Выполнение модели производит следующие изображения осциллографа. Нанесенное на график ошибочное количество будет отличаться на основе значения Initial Seed, используемого в блоке Random Integer Generator. (Чтобы заставить ось расположиться точно соответствие тот из первого осциллографа, щелкните правой кнопкой по области построения по осциллографу и выберите Axes Properties.)
Количество ошибок перед исправлением
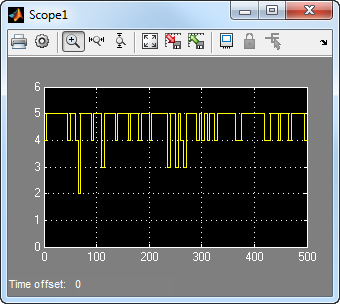
Второй график является количеством ошибок, которые декодер обнаружил при попытке восстановить сообщение. Часто номер равняется пяти, потому что блок Gain заменяет первые пять символов в каждой кодовой комбинации с нулями. Однако количество ошибок - меньше чем пять каждый раз, когда правильная кодовая комбинация содержит один или несколько нулей в первых пяти местах.
Первый график является различием между исходным сообщением и восстановленным сообщением; поскольку декодер смог исправить все ошибки, которые произошли, каждый из этих пяти потоков данных в графике является нулем.
Несмотря на то, что подбиблиотека Block Coding несколько универсальна в своем стили, различные методы кодирования не идентичны. В этом разделе описываются специальные опции и ограничения, которые применяются к параметрам и сигналам для категорий метода кодирования в этой подбиблиотеке. Кодирование методов, обсужденных ниже, включает - Типичный Линейный Блочный код, Циклический код, Код Хемминга, код BCH и код Тростника-Solomon.
Типичные линейные блочные коды
Кодирование сообщения с помощью типичного линейного блочного кода требует порождающей матрицы. Декодирование кода требует порождающей матрицы и возможно таблицы истинности. Чтобы использовать Бинарный Линейный Энкодер и Бинарные Линейные блоки Декодера, необходимо понять параметры Error-correction truth table и Generator matrix.
Порождающая матрица - процесс кодирования сообщения в [N, K] линейный блочный код определяется K-by-N порождающей матрицей G. А именно, 1 вектором сообщения K v закодирован в вектор кодовой комбинации 1 на n vG. Если G имеет форму [Ик, P] или [P, Ик], где P является некоторой матрицей K-by-(N-K), и Ик является K-by-K единичной матрицей, G, как говорят, находится в стандартной форме. (Некоторые авторы, такие как Кларк и Каин [2], используют первую стандартную форму, в то время как другие, такие как Лин и Костелло [3], используют второе.) Линейные блоки блочного кодирования в этом продукте требуют, чтобы параметр маски Generator matrix был в стандартной форме.
При декодировании Таблицы - таблица декодирования говорит декодер, как исправить ошибки, которые, возможно, повредили код во время передачи. Коды Хемминга могут исправить любую односимвольную ошибку в любой кодовой комбинации. Другие коды могут исправить, или частично исправить, ошибки, которые повреждают больше чем один символ в данной кодовой комбинации.
Блок Binary Linear Decoder позволяет вам задавать таблицу декодирования в параметре Error-correction truth table. Представляйте таблицу декодирования как матрицу со столбцами N и строками 2N-K. Каждая строка дает вектор исправления для одного полученного вектора кодовой комбинации.
Можно постараться не задавать таблицу декодирования явным образом путем установки параметра Error-correction truth table на 0. Когда Error-correction truth table является 0, блок вычисляет таблицу декодирования с помощью функции syndtable.
Циклические коды
Для циклических кодов длина кодовой комбинации N должна иметь форму 2M-1, где M является целым числом, больше, чем или равный 3.
Полиномы генератора - Циклические коды имеют специальные алгебраические свойства, которые позволяют полиному определять процесс кодирования полностью. Этот так называемый полином генератора является степенью - (N-K) делитель полинома xN-1. Линт фургона [5] объясняет, как полином генератора определяет циклический код.
Бинарный Циклический Энкодер и Бинарные Циклические блоки Декодера позволяют вам задавать полином генератора как второй параметр маски, вместо того, чтобы задать K там. Блоки представляют полином генератора использование вектора, который перечисляет коэффициенты полинома в порядке возрастающих степеней переменной. Можно найти полиномы генератора для циклических кодов с помощью функции cyclpoly.
Если вы не хотите задавать полином генератора, установите второй параметр маски на значение K.
Коды Хемминга
Для Кодов Хемминга длина кодовой комбинации N должна иметь форму 2M-1, где M является целым числом, больше, чем или равный 3. Длина сообщения K должна равняться N-M.
Примитивные Полиномы - Коды Хемминга полагаются на алгебраические поля, которые имеют 2M элементы (или, в более общем плане, пополудни элементы для простого числа p). Элементы таких полей называют относительно выдающегося элемента поля, которое называется примитивным элементом. Минимальный полином примитивного элемента называется примитивным полиномом. Блоки Декодера Энкодера и Хэмминга Хэмминга позволяют вам задавать примитивный полином для конечного поля, которое они используют для вычислений. Если вы хотите задать этот полином, сделайте так во втором поле параметра маски. Блоки представляют примитивный полином с помощью вектора, который перечисляет коэффициенты полинома в порядке возрастающих степеней переменной. Можно найти полиномы генератора для Полей Галуа с помощью функции gfprimfd.
Если вы не хотите задавать примитивный полином, установите второй параметр маски на значение K.
Коды BCH
Коды BCH являются циклическими кодами с коррекцией ошибок, которые создаются с помощью конечных полей. Для этих кодов длина кодовой комбинации N должна иметь форму 2M-1, где M является целым числом от 3 до 9. Длина сообщения K ограничивается особыми значениями, которые зависят от N. Чтобы видеть, какие значения K допустимы для данного N, смотрите Систему comm.BCHEncoder object™ страница с описанием. Никакая известная аналитическая формула не описывает отношение среди длины кодовой комбинации, длины сообщения и возможности исправления ошибок кодов BCH.
Узкий смысл коды BCH
Полином генератора узкого смысла является LCM [m_1 (x), m_2 (x)..., m_2t (x)], где:
LCM представляет наименьшее общее кратное,
m_i (x) представляет минимальный многочлен, соответствующий αi, α является корнем примитивного полинома по умолчанию для поля GF (n+1),
и t представляет поддержку с коррекцией ошибок кода.
Коды тростника-Solomon
Коды тростника-Solomon полезны для исправления ошибок, которые происходят в пакетах. В самом простом случае длина кодовых комбинаций в коде Тростника-Solomon имеет форму N = 2M-1, где 2M количество символов для кода. Поддержкой исправления ошибок кода Тростника-Solomon является floor((N-K)/2), где K является длиной слов сообщения. Различие N-K должно быть ровным.
Иногда удобно использовать сокращенный код Тростника-Solomon, в котором N является меньше, чем 2M-1. В этом случае энкодер добавляет нулевые символы 2M-1-N к каждому слову сообщения и кодовой комбинации. Поддержкой исправления ошибок сокращенного кода Тростника-Solomon является также floor((N-K)/2). Блоки Тростника-Solomon Communications Toolbox могут реализовать сокращенные коды Тростника-Solomon.
Эффект Небинарных Символов - Одно различие между кодами Тростника-Solomon и другими кодами, поддержанными в этом продукте, состоит в том что символы процесса Тростника-Solomon кода в GF (2M) вместо GF (2). M биты задают каждый символ. Небинарная природа кодовых знаков Тростника-Solomon заставляет блоки Тростника-Solomon отличаться от других кодеров этими способами:
Можно использовать целочисленный формат через Введенный целым числом Энкодер RS и Выведенные целым числом блоки Декодера RS.
Двоичный формат ожидает, что длины вектора будут целочисленным кратным M*K (не K) для сообщений и того же целочисленного M*N (не N) для кодовых комбинаций.
Информация об ошибке - блоки декодирования Тростника-Solomon (Двоичный выход Декодер RS и Выведенный целым числом Декодер RS) возвращают связанную с ошибкой информацию во время симуляции. Второй выходной сигнал указывает на количество ошибок, которые блок обнаружил во входной кодовой комбинации.-1 во втором выводе указывает, что блок обнаружил больше ошибок, чем это могло исправить использование схемы кодирования.
Много стандартов используют проколотые коды, и цифровые получатели могут легко вывести стирания. Производительность BCH и RS значительно улучшается в исчезающих каналах, где получатель генерирует стирания.
Проколотая кодовая комбинация имеет только символы четности, удаленные, и сокращенная кодовая комбинация имеет только информационные удаленные символы. Кодовая комбинация со стираниями может иметь те стирания или в информационных символах или в символах четности.
Примеры Рида Соломона с сокращением, прокалыванием и стираниями
В этом разделе, представительном примере Рида Соломона, кодирующего с сокращением, прокалывание и стирания создаются с увеличивающейся сложностью исправления ошибок.
Пример энкодера с сокращением и прокалыванием
Следующие данные показывают представительный пример (7,3) энкодер Рида Соломона с сокращением и прокалыванием.
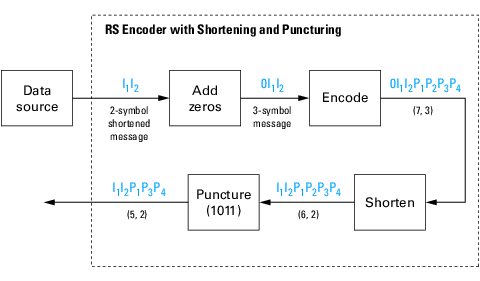
В этой фигуре, источник сообщения выходные параметры два информационных символа, определяемые I1I2. (Для примера BCH символы являются битами.), Поскольку код является сокращенным (7,3) код, нуль должен быть добавлен перед информационными символами, приведя к сообщению с тремя символами 0I1I2. Измененной последовательностью сообщения является RS, закодированный, и добавленный информационный нуль затем удален, который приводит к результату I1I2P1P2P3P4. (В этом примере биты четности в конце кодовой комбинации.)
Операцией прокалывания управляет вектор прокола, который, в этом случае, является 1011. В векторе прокола 1 означает, что символ сохранен, и 0 означает, что символ выброшен. В этом примере операция прокалывания удаляет второй символ четности, приводя к итоговому вектору I1I2P1P3P4.
Пример декодера с сокращением и прокалыванием
Следующие данные показывают, как декодер RS работает с сокращенной и проколотой кодовой комбинацией.
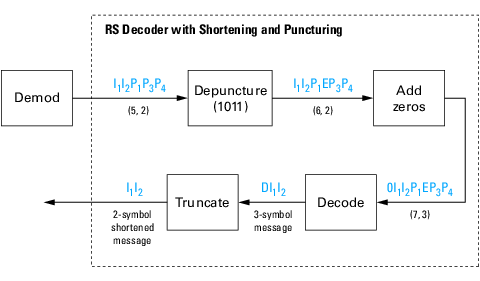
Этот случай соответствует работе энкодера, показанной в фигуре энкодера RS с сокращением и прокалыванием. Как показано в предыдущей фигуре, энкодер получает (5,2) кодовая комбинация, потому что это было сокращено от (7,3) кодовая комбинация одним символом, и один символ был также проколот.
Как первый шаг, декодер добавляет стирание, определяемое E, во втором положении четности кодовой комбинации. Это соответствует вектору прокола 1011. Добавление нуля составляет сокращение, таким же образом как показано в предыдущей фигуре. Одно стирание не превышает исправляющую стирание поддержку кода, который может исправить четыре стирания. Операция декодирования приводит к сообщению DI1I2 с тремя символами. Первый символ является усеченным, как в предыдущей фигуре, приводя к окончательному результату I1I2.
Пример декодера с сокращением, прокалыванием и стираниями
Следующие данные показывают декодер, работающий с проколотой, сокращенной кодовой комбинацией, также исправляя стирания, сгенерированные получателем.
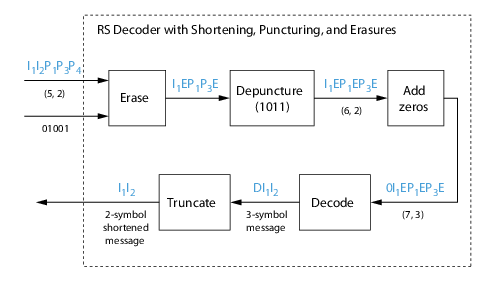
В этой фигуре демодулятор получает вектор I1I2P1P3P4 что отправленный энкодер. Демодулятор объявляет, что два из пяти полученных символов достаточно ненадежны, чтобы быть стертыми, такие, что символы 2 и 5, как считают, являются стираниями. 01 001 вектор, обеспеченный внешним источником, указывает на эти стирания. В векторе стираний 1 означает, что символ должен быть заменен символом стирания и 0 средние значения, что символ передается неизменный.
Блоки декодера получают кодовую комбинацию и вектор стирания, и выполняют стирания, обозначенные вектором 01001. В векторе стираний 1 означает, что символ должен быть заменен символом стирания и 0 средние значения, что символ передается неизменный. Получившийся вектор кодовой комбинации является I1EP1P3E, где E является символом стирания.
Кодовая комбинация затем depunctured, согласно вектору прокола, используемому в операции кодирования (т.е. 1011). Таким образом символ стирания вставляется между P1 и P3, приводя к вектору кодовой комбинации I1EP1EP3E.
Только до декодирования, сложение нулей в начале информационного вектора составляет сокращение. Итоговый вектор является 0I1EP1EP3E, таким, что (7,3) кодовая комбинация отправляется в алгоритм Berlekamp.
Эта кодовая комбинация декодируется, приводя к сообщению с тремя символами DI1I2 (где D относится к фиктивному символу). Наконец, удаление символа D от вектора сообщения составляет сокращение и приводит к исходному I1I2 вектору.
Для получения дополнительной информации смотрите, что Тростник-Solomon Кодирует со Стираниями, Проколами, и Сокращает пример.
Чтобы открыть модель в качестве примера, которая использует код Тростника-Solomon в целочисленном формате, введите doc_rscoding в командной строке MATLAB. Для получения дополнительной информации о модели, смотрите Пример: Код тростника-Solomon в Целочисленном формате
Чтобы найти полином генератора для циклического, BCH или код Тростника-Solomon, используют cyclpoly, bchgenpoly или функцию rsgenpoly, соответственно. Команды
genpolyCyclic = cyclpoly(15,5) % 1+X^5+X^10 genpolyBCH = bchgenpoly(15,5) % x^10+x^8+x^5+x^4+x^2+x+1 genpolyRS = rsgenpoly(15,5)
найдите полиномы генератора для блочных кодов различных типов. Вывод ниже.
genpolyCyclic =
1 0 0 0 0 1 0 0 0 0 1
genpolyBCH = GF(2) array.
Array elements =
1 0 1 0 0 1 1 0 1 1 1
genpolyRS = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
1 4 8 10 12 9 4 2 12 2 7
Форматы этих выходных параметров отличаются:
cyclpoly представляет полином генератора использование целочисленного вектора - строки, который перечисляет коэффициенты полинома в порядке возрастающих степеней переменной.
bchgenpoly и rsgenpoly представляют полином генератора использование вектора - строки Галуа, который перечисляет коэффициенты полинома в порядке убывающих степеней переменной.
rsgenpoly использует коэффициенты в Поле Галуа кроме бинарного поля GF (2). Для получения дополнительной информации о значении этих коэффициентов смотрите, Как Целые числа Соответствуют Элементам Поля Галуа и Полиномам по Полям Галуа.
Групповой из полиномов генератора
Некоторые пары длины сообщения и длины кодовой комбинации исключительно не определяют полином генератора. Синтаксисы для функций в примере выше также включают опции для получения полиномов генератора, которые удовлетворяют определенные ограничения, которые вы задаете. Смотрите страницы с описанием функций для получения дополнительной информации об опциях синтаксиса.
Алгебраическое выражение для полиномов генератора
Полиномы генератора, произведенные bchgenpoly и rsgenpoly, имеют форму (X - Ab) (X - Ab+1)... (X - Ab+2t-1), где A является примитивным элементом для соответствующего Поля Галуа, и b и t, целые числа. Смотрите страницы с описанием функций для получения дополнительной информации об этом выражении.
В этом разделе описываются функции, которые вычисляют типичные параметры, сопоставленные с линейными блочными кодами, а также функциями, которые преобразовывают информацию от одного формата до другого.
Исправление ошибок по сравнению с выявлением ошибок для линейных блочных кодов
Можно использовать линейный блочный код, чтобы обнаружить min d-1 ошибка или исправить t = ошибки.
Если вы ставите под угрозу поддержку исправления ошибок кода, можно обнаружить больше, чем ошибки t. Например, код с min d = 7 может исправить t = 3 ошибки, или это может обнаружить до 4 ошибок и исправить до 2 ошибок.
Нахождение возможности исправления ошибок
bchgenpoly и функции rsgenpoly могут возвратить дополнительный второй выходной аргумент, который указывает на возможность исправления ошибок кода Тростника-Solomon или BCH. Например, команды
[g,t] = bchgenpoly(31,16);
t
t =
3
найдите, что [31, 16] код BCH может исправить до трех ошибок в каждой кодовой комбинации.
Нахождение матриц генератора и проверки четности
Чтобы найти проверку четности и порождающую матрицу для Кода Хемминга с длиной кодовой комбинации 2^m-1, используйте функцию hammgen как ниже. m должен быть по крайней мере тремя.
[parmat,genmat] = hammgen(m); % Hamming
Чтобы найти проверку четности и порождающую матрицу для циклического кода, используйте функцию cyclgen. Необходимо обеспечить длину кодовой комбинации и допустимый полином генератора. Можно использовать функцию cyclpoly, чтобы произвести один возможный полином генератора после того, как вы обеспечите длина сообщения и длина кодовой комбинации. Например,
[parmat,genmat] = cyclgen(7,cyclpoly(7,4)); % CyclicПреобразование между матрицами проверки четности и генератора
Функция gen2par преобразовывает порождающую матрицу в матрицу проверки четности, и наоборот. Страница с описанием для gen2par содержит примеры, чтобы проиллюстрировать это.
[1] Berlekamp, Элвин Р., Алджебрэйк-Кодинг-Зэори, Нью-Йорк, McGraw-Hill, 1968.
[2] Кларк, Джордж К. Младший, и J. Затвор Каин, кодирование с коррекцией ошибок для цифровой связи, Нью-Йорка, нажатия пленума, 1981.
[3] Лин, Шу, и Дэниел Дж. Костелло младший, кодирование контроля ошибок: основные принципы и приложения, Englewood Cliffs, NJ, Prentice Hall, 1983.
[4] Петерсон, В. Уэсли, и Э. Дж. Уэлдон младший, Коды С коррекцией ошибок, 2-й редактор, Кембридж, MA, Нажатие MIT, 1972.
[5] Линт фургона, J. H. Введение в Кодинг-Зэори, Нью-Йорк, Springer-Verlag, 1982.
[6] Ивовый прут, Стивен Б., системы контроля ошибок для цифровой связи и устройства хранения данных, верхнего Сэддл-Ривер, NJ, Prentice Hall, 1995.
[7] Gallager, Роберт Г., имеющие малую плотность коды с проверкой четности, Кембридж, MA, нажатие MIT, 1963.
[8] Райан, Уильям Э., “Введение в коды LDPC”, Кодируя и Обработку сигналов для Магнитных Систем Перекодирования (Vasic, B., редактор), Нажатие CRC, 2004.
Разработайте Уровень 2/3 Feedforward Энкодер Используя Simulink
Реализуйте систематический энкодер с обратной связью Используя Simulink
Сверточное кодирование является особым случаем кодирования контроля ошибок. В отличие от кодера блока, сверточный кодер не является устройством без памяти. Даже при том, что сверточный кодер принимает постоянное число символов сообщения и производит постоянное число кодовых знаков, его вычисления зависят не только от текущего набора вводимых символов, но и на некоторых предыдущих вводимых символах.
Communications Toolbox предусматривает сверточные возможности кодирования как блоки Simulink, Системные объекты и функции MATLAB. Это поддержка продукта feedforward и сверточные коды обратной связи, которые могут быть описаны структурой решетки или набором полиномов генератора. Это использует алгоритм Viterbi, чтобы реализовать декодирование трудного решения и мягкого решения.
Продукт также включает по опыту декодер вероятности, который может использоваться для мягкого выходного декодирования сверточных кодов.
Для справочной информации о сверточном кодировании смотрите работы, перечисленные в Выбранной Библиографии для Сверточного Кодирования.
Параметры блоков для сверточного кодирования
К сверточным кодам процесса используйте Сверточный Энкодер, Декодер Витерби и/или блоки Декодера APP в подбиблиотеке Convolutional. Если параметр маски требуется и в энкодере и в декодере, используйте то же значение в обоих блоках.
Блоки в подбиблиотеке Convolutional принимают, что вы используете одно из двух различных представлений сверточного энкодера:
Если вы разрабатываете свой энкодер с помощью схемы со сдвиговыми регистрами и по модулю 2 сумматорами, можно вычислить матрицу полинома генератора кода и впоследствии использовать функцию poly2trellis (в Communications Toolbox), чтобы сгенерировать соответствующий параметр маски структуры решетки автоматически. Для примера см. Проект Уровень 2/3 Feedforward Энкодер Используя Simulink.
Если вы разрабатываете свой энкодер с помощью схемы решетки, можно создать структуру решетки в MATLAB и использовать его в качестве параметра маски.
Для получения дополнительной информации об этих представлениях, см. Полиномиальное Описание Описания Сверточного кода и Решетки Сверточного кода.
Используя полиномиальное описание в блоках
Чтобы использовать полиномиальное описание со Сверточным Энкодером, Декодер Витерби или блоки Декодера APP, использует служебную функцию poly2trellis от Communications Toolbox. Эта функция принимает полиномиальное описание и преобразовывает его в описание решетки. Например, следующая команда вычисляет описание решетки энкодера, продолжительность ограничения которого равняется 5 и чьи полиномы генератора равняются 35 и 31:
trellis = poly2trellis(5,[35 31]);
Чтобы использовать этот энкодер с одним из сверточных кодеров, просто поместите команду poly2trellis такой как
poly2trellis(5,[35 31]);
в поле параметра Trellis structure.
Полиномиальное описание сверточного энкодера описывает связи среди сдвиговых регистров и по модулю 2 сумматоров. Например, фигура ниже изображает feedforward сверточный энкодер, который имеет вход того, два выходных параметров и два сдвиговых регистра.
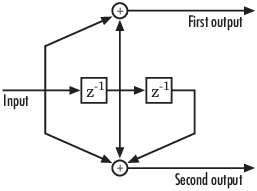
Полиномиальное описание сверточного энкодера имеет или два или три компонента, в зависимости от того, является ли энкодер типом обратной связи или feedforward:
Полиномы связи обратной связи (только для энкодеров обратной связи)
Продолжительности ограничения. Продолжительности ограничения энкодера формируют вектор, длина которого является количеством входных параметров в схеме энкодера. Элементы этого вектора указывают на количество битов, сохраненных в каждом сдвиговом регистре, включая текущие входные биты.
В фигуре выше, продолжительность ограничения равняется трем. Это - скаляр, потому что энкодер имеет входной поток того, и его значение один плюс количество сдвиговых регистров для того входа.
Полиномы генератора. Если схема энкодера имеет входные параметры k и n выходные параметры, матрица генератора кода является k-by-n матрицей. Элемент в ith строке и jth столбце указывает, как вход ith вносит в jth вывод.
Для систематических битов систематического энкодера обратной связи совпадайте с записью в матрице генератора кода с соответствующим элементом вектора связи обратной связи. Смотрите Полиномы Связи Обратной связи ниже для деталей.
В других ситуациях можно определить (i, j) запись в матрице можно следующим образом:
Создайте представление двоичного числа путем размещения 1 в каждое пятно, где строка связи от сдвигового регистра питается в сумматор и 0 в другом месте. Крайнее левое пятно в двоичном числе представляет текущий вход, в то время как самое правое пятно представляет самый старый вход, который все еще остается в сдвиговом регистре.
Преобразуйте это бинарное представление в восьмеричное представление путем рассмотрения последовательных триплетов битов, запуска с самого правого бита. Самый правый бит в каждом триплете младше значащий. Если количество битов не является кратным три, нулевые биты места в левом конце по мере необходимости. (Например, интерпретируйте 1101010 как 001 101 010 и преобразуйте его в 152.)
Например, двоичные числа, соответствующие верхним и более низким сумматорам в фигуре выше, равняются 110 и 111, соответственно. Эти двоичные числа эквивалентны восьмеричным числам 6 и 7, соответственно, таким образом, матрица полинома генератора [6 7].
Можно выполнить преобразование из двоичной системы в восьмеричную в MATLAB при помощи кода как str2num(dec2base(bin2dec('110'),8)).
Для таблицы некоторых хороших генераторов сверточного кода обратитесь к [2] в разделе Selected Bibliography for Block Coding, особенно что приложения книги.
Полиномы Связи обратной связи. Если вы представляете энкодер обратной связи, вам нужен вектор полиномов связи обратной связи. Длина этого вектора является количеством входных параметров в схеме энкодера. Элементы этого вектора указывают на связь обратной связи для каждого входа, с помощью восьмеричного формата. Сначала создайте представление двоичного числа как на шаге 1 выше. Затем преобразуйте бинарное представление в восьмеричное представление как на шаге 2 выше.
Если энкодер имеет настройку обратной связи и также систематичен, генератор кода и параметры связи обратной связи, соответствующие систематическим битам, должны иметь те же значения.
Структура решетки для 1/2 Обратной связи Сверточный Энкодер
Создайте структуру решетки для уровня 1/2 систематический сверточный энкодер с обратной связью, которую показывают. Используйте решетку, чтобы закодировать и декодировать случайный поток битов.

Этот энкодер имеет продолжительность ограничения 5, матрицу полинома генератора [37 33], и полином связи обратной связи 37.
Первый полином генератора совпадает с полиномом связи обратной связи, потому что первый вывод соответствует систематическим битам. Полином обратной связи представлен бинарным вектором [1 1 1 1 1], соответствуя верхней строке двоичных цифр в схеме. Эти цифры указывают на связи от выходных параметров регистров к сумматору. Начальный 1 соответствует входному биту. Восьмеричное представление двоичного числа 11111 равняется 37.
Второй полином генератора представлен бинарным вектором [1 1 0 1 1], соответствуя более низкой строке двоичных цифр в схеме. Восьмеричное число, соответствующее двоичному числу 11011, равняется 33.
Используйте poly2trellis, чтобы преобразовать полином в структуру решетки. Когда используется с полиномом обратной связи, poly2trellis устанавливает связь обратной связи с входом решетки.
trellis = poly2trellis(5, [37 33], 37)
trellis = struct with fields:
numInputSymbols: 2
numOutputSymbols: 4
numStates: 16
nextStates: [16x2 double]
outputs: [16x2 double]
Сгенерируйте случайные двоичные данные, convolutionally закодируйте данные и декодируйте данные с помощью алгоритма Viterbi.
data = randi([0 1],70,1); codedData = convenc(data,trellis); decodedData = vitdec(codedData,trellis,34,'trunc','hard');
Проверьте, что декодируемые данные не имеют никаких битовых ошибок.
biterr(data,decodedData)
ans = 0
Используя Полиномиальное Описание в MATLAB. Чтобы использовать полиномиальное описание с функциями convenc и vitdec, сначала преобразуйте его в описание решетки с помощью функции poly2trellis. Например, команда ниже вычисляет описание решетки энкодера, изображенного в разделе Polynomial Description Сверточного кода.
trellis = poly2trellis(3,[6 7]);
Структура MATLAB trellis является подходящим входным параметром для convenc и vitdec.
Описание решетки сверточного энкодера показывает, как каждый возможный вход к энкодеру влияет и на вывод и на изменения состояния энкодера. В этом разделе описываются решетки, и как представлять решетки в MATLAB и дает пример решетки MATLAB.
Фигура ниже изображает решетку для сверточного энкодера от предыдущего раздела. Энкодер имеет четыре состояния (пронумерованный в двоичном файле от 00 до 11), однобитный вход и двухбитовый вывод. (Отношение входных битов, чтобы вывести биты делает этот энкодер rate-1/2 энкодер.) Каждая твердая стрелка показывает, как энкодер изменяет свое состояние, если текущий вход является нулем, и каждая пунктирная стрелка показывает, как энкодер изменяет свое состояние, если текущий вход является тем. Восьмеричные числа выше каждой стрелки указывают на текущую производительность энкодера.
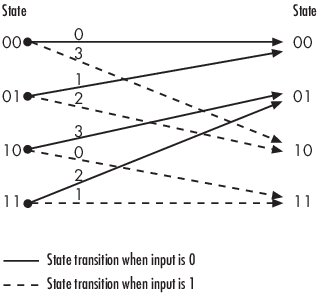
Как пример интерпретации этой схемы решетки, если энкодер находится в этих 10 состояниях и получает вход нуля, это выводит кодовый знак 3 и изменяется на это 01 состояние. Если это находится в этих 10 состояниях и получает вход одного, это выводит кодовый знак 0 и изменяется на эти 11 состояний.
Обратите внимание на то, что любое полиномиальное описание сверточного энкодера эквивалентно некоторому описанию решетки, несмотря на то, что некоторые решетки не имеют никаких соответствующих полиномиальных описаний.
Определение Решетки в MATLAB. Чтобы задать решетку в MATLAB, используйте определенную форму структуры MATLAB, названной структурой решетки. Структура решетки должна иметь пять полей, как в приведенной ниже таблице.
Поля Структуры Решетки для Уровня k/n Код
| Поле в структуре решетки | Размерности | Значение |
|---|---|---|
numInputSymbols
| Скаляр | Количество вводимых символов к энкодеру: 2k |
numOutputsymbols
| Скаляр | Количество выходных символов от энкодера: 2n |
numStates
| Скаляр | Количество состояний в энкодере |
nextStates
| numStates-by-2k матрица | Следующие состояния для всех комбинаций текущего состояния и текущего входа |
outputs
| numStates-by-2k матрица | Выходные параметры (в восьмеричном) для всех комбинаций текущего состояния и текущего входа |
В то время как ваша структура решетки может иметь любое имя, его поля должны иметь точные имена как в таблице. Имена полей являются чувствительными к регистру.
В матрице nextStates каждая запись является целым числом между 0 и numStates-1. Элемент в ith строке и jth столбце обозначает следующее состояние, когда начальное состояние является i-1, и входные биты имеют десятичное представление j-1. Чтобы преобразовать входные биты в десятичное значение, используйте первый входной бит в качестве старшего значащего бита (MSB). Например, второй столбец матрицы nextStates хранит следующие состояния, когда текущий набор входных значений {0..., 0,1}. Чтобы изучить, как присвоить номера состояниям, смотрите страницу с описанием для istrellis.
В матрице outputs элемент в ith строке и jth столбце обозначает вывод энкодера, когда начальное состояние является i-1, и входные биты имеют десятичное представление j-1. Чтобы преобразовать в десятичное значение, используйте первый выходной бит в качестве MSB.
Как Создать Структуру Решетки MATLAB. Если вы знаете, какую информацию вы хотите поместить в каждое поле, можно создать структуру решетки любым из этих способов:
Задайте каждое из этих пяти полей индивидуально, с помощью обозначения structurename.fieldname. Например, установите первое поле структуры под названием s с помощью команды ниже. Используйте дополнительные команды, чтобы задать другие поля.
s.numInputSymbols = 2;
Страница с описанием для функции istrellis иллюстрирует этот подход.
Соберите все имена полей и их значения в одной команде struct. Например:
s = struct('numInputSymbols',2,'numOutputSymbols',2,...
'numStates',2,'nextStates',[0 1;0 1],'outputs',[0 0;1 1]);
Запустите с полиномиального описания энкодера и используйте функцию poly2trellis, чтобы преобразовать его в допустимую структуру решетки. Для получения дополнительной информации см. Полиномиальное Описание Сверточного кода.
Чтобы проверять, является ли ваша структура допустимой структурой решетки, используйте функцию istrellis.
Пример: Структура Решетки MATLAB. Считайте решетку показанной ниже.

Чтобы создать структуру решетки, которая описывает его, используйте команду ниже.
trellis = struct('numInputSymbols',2,'numOutputSymbols',4,... 'numStates',4,'nextStates',[0 2;0 2;1 3;1 3],... 'outputs',[0 3;1 2;3 0;2 1]);
Количество вводимых символов равняется 2, потому что схема решетки имеет два типа входа path: твердая стрелка и пунктирная стрелка. Количество выходных символов равняется 4, потому что числа выше стрелок могут быть или 0, 1, 2, или 3. Количество состояний равняется 4, потому что существует четыре маркера на левой стороне схемы решетки (эквивалентно, четыре на правой стороне). Чтобы вычислить матрицу следующих состояний, создайте матрицу, строки которой соответствуют этим четырем текущим состояниям на левой стороне решетки, столбцы которой соответствуют входным параметрам 0 и 1, и чьи элементы дают следующие состояния в конце стрелок на правой стороне решетки. Чтобы вычислить матрицу выходных параметров, создайте матрицу, строки и столбцы которой как в следующей матрице состояний, но чьи элементы дают восьмеричные выходные параметры, показанные выше стрелок в решетке.
Функциями для кодирования и декодирования сверточных кодов является convenc и vitdec. В этом разделе рассматриваются использование этих функций, чтобы создать и декодировать сверточные коды.
Кодирование. Простой способ использовать convenc, чтобы создать сверточный код показывают в командах ниже.
Задайте решетку.
t = poly2trellis([4 3],[4 5 17;7 4 2]);
Закодируйте вектор из единиц.
x = ones(100,1); code = convenc(x,t);
Первая команда преобразовывает полиномиальное описание feedforward сверточного энкодера к соответствующему описанию решетки. Вторая команда кодирует 100 битов, или 50 двухбитовых символов. Поскольку уровень кода в этом примере является 2/3, выходной вектор, code содержит 150 битов (то есть, 100 входных раз битов 3/2).
Чтобы проверять, соответствует ли ваша решетка катастрофическому сверточному коду, используйте функцию iscatastrophic.
Декодирование трудного решения. Чтобы декодировать трудные решения использования, используйте функцию vitdec с флагом 'hard' и с данными о двоичном входе. Поскольку вывод convenc является бинарным декодирование трудного решения может использовать вывод convenc непосредственно без дополнительной обработки. Этот пример расширяет предыдущий пример и реализует декодирование трудного решения.
Задайте решетку.
t = poly2trellis([4 3],[4 5 17;7 4 2]);
Закодируйте вектор из единиц.
code = convenc(ones(100,1),t);
Установите traceback длину для декодирования и декодируйте использование vitdec.
tb = 2; decoded = vitdec(code,t,tb,'trunc','hard');
Проверьте, что декодируемые данные являются вектором из 100 единиц.
isequal(decoded,ones(100,1))
ans = logical
1
Декодирование мягкого решения. Чтобы декодировать использующие мягкие решения, используйте функцию vitdec с флагом 'soft'. Задайте номер, nsdec, битов мягкого решения и используйте входные данные, состоящие из целых чисел между 0 и 2^nsdec-1.
Вход 0 представляет самый уверенный 0, в то время как вход 2^nsdec-1 представляет самый уверенный 1. Другие значения представляют менее уверенные решения. Например, таблица ниже приводит интерпретации значений для 3-битных мягких решений.
Входные значения для 3-битных мягких решений
| Входное значение | Интерпретация |
|---|---|
| 0 | Самый уверенный 0 |
| 1 | Второй самый уверенный 0 |
| 2 | Третий самый большой уверенный 0 |
| 3 | Наименее уверенный 0 |
| 4 | Наименее уверенный 1 |
| 5 | Третий самый большой уверенный 1 |
| 6 | Второй самый уверенный 1 |
| 7 | Самый уверенный 1 |
Реализуйте декодирование Мягкого Решения Используя MATLAB
Скрипт ниже иллюстрирует декодирование с 3-битными мягкими решениями. Сначала это создает сверточный код с convenc и добавляет белый Гауссов шум в код с awgn. Затем чтобы подготовиться к декодированию мягкого решения, пример использует quantiz, чтобы сопоставить шумные значения данных с соответствующими целыми числами значения решения между 0 и 7. Второй аргумент в quantiz является вектором раздела, который определяет, который значения данных сопоставляют с 0, 1, 2, и т.д. Раздел выбран так, чтобы значения около 0 карт к 0 и значения около 1 карты к 7. (Можно совершенствовать раздел, чтобы получить лучше декодирующую производительность, если приложение требует его.) Наконец, пример декодирует код и вычисляет частоту ошибок по битам. При сравнении декодируемых данных с исходным сообщением пример должен принять задержку декодирования во внимание. Непрерывный режим работы vitdec вызывает задержку, равную traceback длине, таким образом, msg(1) соответствует decoded(tblen+1), а не decoded(1).
s = RandStream.create('mt19937ar', 'seed',94384); prevStream = RandStream.setGlobalStream(s); msg = randi([0 1],4000,1); % Random data t = poly2trellis(7,[171 133]); % Define trellis. % Create a ConvolutionalEncoder System object hConvEnc = comm.ConvolutionalEncoder(t); % Create an AWGNChannel System object. hChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)',... 'SNR', 6); % Create a ViterbiDecoder System object hVitDec = comm.ViterbiDecoder(t, 'InputFormat', 'Soft', ... 'SoftInputWordLength', 3, 'TracebackDepth', 48, ... 'TerminationMethod', 'Continuous'); % Create a ErrorRate Calculator System object. Account for the receive % delay caused by the traceback length of the viterbi decoder. hErrorCalc = comm.ErrorRate('ReceiveDelay', 48); ber = zeros(3,1); % Store BER values code = step(hConvEnc,msg); % Encode the data. hChan.SignalPower = (code'*code)/length(code); ncode = step(hChan,code); % Add noise. % Quantize to prepare for soft-decision decoding. qcode = quantiz(ncode,[0.001,.1,.3,.5,.7,.9,.999]); tblen = 48; delay = tblen; % Traceback length decoded = step(hVitDec,qcode); % Decode. % Compute bit error rate. ber = step(hErrorCalc, msg, decoded); ratio = ber(1) number = ber(2) RandStream.setGlobalStream(prevStream);
Вывод ниже.
number =
5
ratio =
0.0013
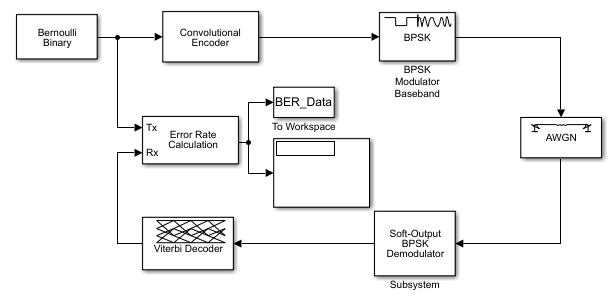
Реализуйте Декодирование Мягкого Решения Используя Simulink. Этот пример создает уровень 1/2 сверточный код. Это использует квантизатор и блок Viterbi Decoder, чтобы выполнить декодирование мягкого решения. Чтобы открыть модель, введите doc_softdecision в командной строке MATLAB. Для описания модели см. Обзор Симуляции.
Определение сверточного кода
feedforward сверточный энкодер в этом примере изображен ниже.
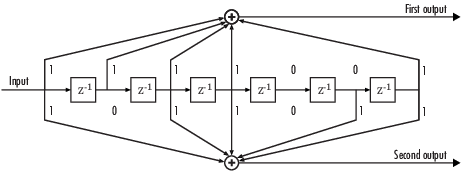
Продолжительность ограничения энкодера является скаляром, поскольку энкодер имеет вход того. Значение продолжительности ограничения является количеством битов, сохраненных в сдвиговом регистре, включая текущий вход. Существует шесть регистров памяти, и текущий вход составляет один бит. Таким образом продолжительность ограничения кода равняется 7.
Генератор кода 1 2 матрица восьмеричных чисел, потому что энкодер имеет вход того и два выходных параметров. Первый элемент в матрице указывает, какие входные значения способствуют первому выводу, и второй элемент в матрице указывает, какие входные значения способствуют второму выводу.
Например, первый вывод в схеме энкодера является 2 суммами по модулю самого правого и четырьмя крайними левыми элементами в массиве схемы входных значений. Семиразрядное двоичное число 1111001 получает эту информацию и эквивалентно восьмеричному числу 171. Восьмеричное число 171 таким образом становится первой записью матрицы генератора кода. Здесь, каждый триплет битов использует крайний левый бит в качестве старшего значащего бита. Второй вывод соответствует двоичному числу 1011011, которое эквивалентно восьмеричному числу 133. Генератор кода поэтому [171 133].
Параметр Trellis structure в блоке Convolutional Encoder говорит блок который код использовать при обработке данных. В этом случае функция poly2trellis, в Communications Toolbox, преобразовывает продолжительность ограничения и пару восьмеричных чисел в допустимую структуру решетки.
В то время как данные о сообщении, вводящие блок Convolutional Encoder, являются скалярным потоком битов, закодированные данные, оставляя блок являются потоком бинарных векторов длины 2.
Отображение полученных данных
Полученные данные, то есть, вывод блока AWGN Channel, состоят из комплексных чисел, которые являются близко к-1 и 1. В порядке восстановить исходное двоичное сообщение, часть получателя модели должна декодировать сверточный код. Блок Viterbi Decoder в этой модели ожидает, что ее входные данные будут целыми числами между 0 и 7. Демодулятор, пользовательская подсистема в этой модели, преобразовывает полученные данные в формат, который блок Viterbi Decoder может интерпретировать правильно. А именно, подсистема демодулятора
Преобразовывает полученный сигнал данных в действительный сигнал путем удаления его мнимой части. Разумно принять, что мнимая часть полученных данных не содержит важную информацию, потому что мнимая часть передаваемых данных является нулем (игнорирование небольших ошибок округления) и потому что шум канала не очень мощен.
Нормирует полученные данные путем деления на стандартное отклонение шумовой оценки и затем умножения на-1.
Квантует нормированные данные с помощью трех битов.
Комбинация этого отображения и отображения решения блока Viterbi Decoder инвертирует модуляцию BPSK, которую блок BPSK Modulator Baseband выполняет на стороне передачи этой модели. Чтобы исследовать подсистему демодулятора более подробно, дважды кликните, значок маркировал Soft-Output BPSK Demodulator.
Декодирование сверточного кода
После того, как полученные данные правильно сопоставлены с длиной 2 вектора 3-битных значений решения, блок Viterbi Decoder декодирует его. Блок использует мягкий алгоритм выбора решения с 23 различными входными значениями, потому что параметром Decision type является Soft Decision, и параметром Number of soft decision bits является 3.
Интерпретация мягкого решения данных
Когда параметр Decision type устанавливается на Soft Decision, блок Viterbi Decoder требует входных значений между 0 и 2b-1, где b является параметром Number of soft decision bits. Блок интерпретирует 0 как самое уверенное решение, что бит кодовой комбинации является 0 и интерпретирует 2b-1 как самое уверенное решение, что бит кодовой комбинации является 1. Значения, промежуточные эти экстремальные значения, представляют менее уверенные решения. В следующей таблице перечислены интерпретации восьми возможных входных значений для этого примера.
| Значение решения | Интерпретация |
|---|---|
| 0 | Самый уверенный 0 |
| 1 | Второй самый уверенный 0 |
| 2 | Третий самый большой уверенный 0 |
| 3 | Наименее уверенный 0 |
| 4 | Наименее уверенный 1 |
| 5 | Третий самый большой уверенный 1 |
| 6 | Второй самый уверенный 1 |
| 7 | Самый уверенный 1 |
Traceback и Decoding Delay
Параметр Traceback depth в блоке Viterbi Decoder представляет длину задержки декодирования. Типичные значения для traceback глубины являются приблизительно пять или шесть раз продолжительностью ограничения, которая была бы 35 или 42 в этом примере. Однако некоторые аппаратные реализации предлагают опции 48 и 96. Этот пример выбирает 48, потому что это ближе к целям (35, и 42), чем 96.
Задержка полученных данных
Параметр Receive delay блока Error Rate Calculation является ненулевым, потому что данный бит сообщения и его соответствующий восстановленный бит разделяются вовремя ненулевой суммой времени симуляции. Параметр Receive delay говорит блок который элементы его входных сигналов выдержать сравнение при проверке ошибок.
В этом случае Получить значение задержки равно значению глубины Traceback (48).
Сравнение результатов симуляции с теоретическими результатами
В этом разделе описывается сравнить частоту ошибок по битам в этой симуляции с частотой ошибок по битам, которая теоретически следовала бы из неквантованного декодирования. Процесс включает эти шаги
Вычисление теоретических границ для частоты ошибок по битам
Чтобы вычислить теоретические границы для Свинца частоты ошибок по битам сверточного кода в этой модели, можно использовать эту оценку на основе декодирования неквантованного решения:
В этой оценке CD является суммой битовых ошибок для ошибочных событий расстояния d, и f является свободным расстоянием кода. Фунт количества является попарной вероятностью появления ошибки, данной
где R является уровнем кода 1/2, и erfc является MATLAB дополнительная функция ошибок, заданная
Значения для содействующего CD и свободного расстояния f находятся в опубликованных статьях, таких как Frenger, P., П. Ортен и Т. Оттоссон, "Коды свертки с Оптимальным Спектром Расстояния", Коммуникационные Буквы IEEE, издание 3, стр 317-319, ноябрь 1999. [3]. Свободное расстояние для этого кода является f = 10.
Следующие команды вычисляют значения Свинца для значений Eb/N0 в диапазоне от 1 до 4 с шагом 0,5:
EbNoVec = [1:0.5:4.0]; R = 1/2; % Errs is the vector of sums of bit errors for % error events at distance d, for d from 10 to 29. Errs = [36 0 211 0 1404 0 11633 0 77433 0 502690 0,... 3322763 0 21292910 0 134365911 0 843425871 0]; % P is the matrix of pairwise error probilities, for % Eb/No values in EbNoVec and d from 10 to 29. P = zeros(20,7); % Initialize. for d = 10:29 P(d-9,:) = (1/2)*erfc(sqrt(d*R*10.^(EbNoVec/10))); end % Bounds is the vector of upper bounds for the bit error % rate, for Eb/No values in EbNoVec. Bounds = Errs*P;
Симуляция многократно, чтобы собрать частоты ошибок по битам
Можно эффективно отличаться параметры симуляции при помощи функции sim, чтобы запустить симуляцию из командной строки MATLAB. Например, следующий код вычисляет частоту ошибок по битам в отношениях энергии, подведенной к долоту к шуму в пределах от 1 дБ к 4 дБ с шагом 0,5 дБ. Это собирает все частоты ошибок по битам из этих симуляций в матричном BERVec. Это также строит частоты ошибок по битам в окне рисунка наряду с теоретическими границами, вычисленными в предыдущем фрагменте кода.
Сначала откройте модель путем нажатия здесь в Браузере документации MATLAB. Затем выполните эти команды, которые могут занять несколько минут.
% Plot theoretical bounds and set up figure. figure; semilogy(EbNoVec,Bounds,'bo',1,NaN,'r*'); xlabel('Eb/No (dB)'); ylabel('Bit Error Rate'); title('Bit Error Rate (BER)'); legend('Theoretical bound on BER','Actual BER'); axis([1 4 1e-5 1]); hold on; BERVec = []; % Make the noise level variable. set_param('doc_softdecision/AWGN Channel',... 'EsNodB','EbNodB+10*log10(1/2)'); % Simulate multiple times. for n = 1:length(EbNoVec) EbNodB = EbNoVec(n); sim('doc_softdecision',5000000); BERVec(n,:) = BER_Data; semilogy(EbNoVec(n),BERVec(n,1),'r*'); % Plot point. drawnow; end hold off;
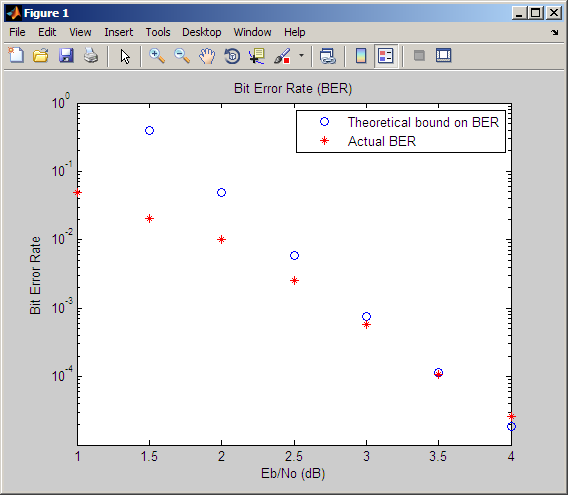
Оценка для Свинца принимает, что декодер использует неквантованные данные, то есть, бесконечно прекрасное квантование. В отличие от этого, симуляция в этом примере использует 8-уровневое (3-битное) квантование. Из-за этого квантования моделируемая частота ошибок по битам является не совсем настолько же низкой как связанное, когда отношение сигнал-шум высоко.
График частоты ошибок по битам против отношения сигнал-шум следует. Местоположения ваших фактических точек BER могут отличаться, потому что симуляция включает случайные числа.
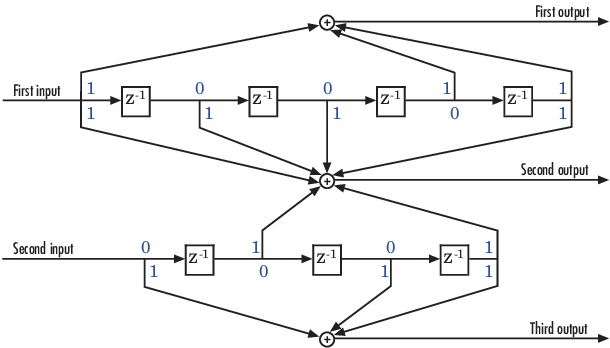
Пример ниже использует уровень 2/3 feedforward энкодер, изображенный в этом схематичном. Сопроводительное описание объясняет, как определить параметр структуры решетки от схематического из энкодера и затем как выполнить кодирование с помощью этого энкодера.
Определение Параметров Кодирования. convenc и функции vitdec могут реализовать этот код, если их параметры имеют соответствующие значения.
Продолжительность ограничения энкодера является вектором длины 2, потому что энкодер имеет два входных параметров. Элементы этого вектора указывают на количество битов, сохраненных в каждом сдвиговом регистре, включая текущие входные биты. Подсчет пространств памяти в каждом сдвиговом регистре в схеме и добавление один для текущих входных параметров приводят к продолжительности ограничения [5 4].
Чтобы определить параметр генератора кода как 2 3 матрица восьмеричных чисел, используйте элемент в ith строке и jth столбце, чтобы указать, как вход ith вносит в jth вывод. Например, чтобы вычислить элемент во второй строке и третьем столбце, крайнее левое и два самых правых элемента во втором сдвиговом регистре схемы питаются в сумму, которая формирует третий вывод. Получите эту информацию как двоичное число 1011, которое эквивалентно восьмеричному числу 13. Полная стоимость матрицы генератора кода [23 35 0; 0 5 13].
Чтобы использовать продолжительность ограничения и параметры генератора кода в convenc и функциях vitdec, используйте функцию poly2trellis, чтобы преобразовать те параметры в структуру решетки. Команда, чтобы сделать это ниже.
trel = poly2trellis([5 4],[23 35 0;0 5 13]); % Define trellis.
Используя Энкодер. Ниже скрипт, который использует этот энкодер.
len = 1000; msg = randi([0 1],2*len,1); % Random binary message of 2-bit symbols trel = poly2trellis([5 4],[23 35 0;0 5 13]); % Trellis % Create a ConvolutionalEncoder System object hConvEnc = comm.ConvolutionalEncoder(trel); % Create a ViterbiDecoder System object hVitDec = comm.ViterbiDecoder(trel, 'InputFormat', 'hard', ... 'TracebackDepth', 34, 'TerminationMethod', 'Continuous'); % Create a ErrorRate Calculator System object. Since each symbol represents % two bits, the receive delay for this object is twice the traceback length % of the viterbi decoder. hErrorCalc = comm.ErrorRate('ReceiveDelay', 68); ber = zeros(3,1); % Store BER values code = step(hConvEnc,msg); % Encode the message. ncode = rem(code + randerr(3*len,1,[0 1;.96 .04]),2); % Add noise. decoded = step(hVitDec, ncode); % Decode. ber = step(hErrorCalc, msg, decoded);
convenc принимает вектор, содержащий 2-битные символы, и производит вектор, содержащий 3-битные символы, в то время как vitdec делает противоположное. Также заметьте, что biterr игнорирует первые 68 элементов decoded. Таким образом, задержка декодирования равняется 68, который является количеством битов на символ (2) из восстановленных времен сообщения traceback значение глубины (34) в функции vitdec. Первые 68 элементов decoded являются 0s, в то время как последующие элементы представляют декодируемые сообщения.
Этот пример использует уровень 2/3 feedforward сверточный энкодер, изображенный в следующей фигуре. Описание объясняет, как определить параметры кодеров от схематического из уровня 2/3 feedforward энкодер. Этот пример также иллюстрирует использование блока Error Rate Calculation с получить задержкой.

Как Определить Параметры Кодирования. Сверточные блоки Энкодера и Декодера Витерби могут реализовать этот код, если их параметры имеют соответствующие значения.
Продолжительность ограничения энкодера является вектором длины 2, поскольку энкодер имеет два входных параметров. Элементы этого вектора указывают на количество битов, сохраненных в каждом сдвиговом регистре, включая текущие входные биты. Подсчет пространств памяти в каждом сдвиговом регистре в схеме и добавление один для текущих входных параметров приводят к продолжительности ограничения [5 4].
Чтобы определить параметр генератора кода как 2 3 матрица восьмеричных чисел, используйте элемент в ith строке и jth столбце, чтобы указать, как вход ith вносит в jth вывод. Например, чтобы вычислить элемент во второй строке и третьем столбце, заметьте, что крайнее левое и два самых правых элемента во втором сдвиговом регистре схемы питаются в сумму, которая формирует третий вывод. Получите эту информацию как двоичное число 1011, которое эквивалентно восьмеричному числу 13. Полная стоимость матрицы генератора кода [27 33 0; 0 5 13].
Чтобы использовать продолжительность ограничения и параметры генератора кода в Сверточных блоках Энкодера и Декодера Витерби, используйте функцию poly2trellis, чтобы преобразовать те параметры в структуру решетки.
Как Моделировать Энкодер. Следующая модель моделирует этот энкодер.

Чтобы открыть завершенную модель, введите doc_convcoding в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:
Бернуллиевый Бинарный Генератор, в библиотеке Comm Sources
Установите Probability of a zero на .5.
Установите Initial seed на любой положительный целочисленный скаляр, предпочтительно вывод функции randn.
Установите Sample time на .5.
Проверяйте флажок Frame-based outputs.
Установите Samples per frame на 2.
Установите Trellis structure на poly2trellis([5 4],[23 35 0; 0 5 13]).
Бинарный Симметричный Канал, в библиотеке Channels
Установите Error probability на 0.02.
Установите Initial seed на любой положительный целочисленный скаляр, предпочтительно вывод функции randn.
Снимите флажок Output error vector .
Установите Trellis structure на poly2trellis([5 4],[23 35 0; 0 5 13]).
Установите Decision type на Hard decision.
Вычисление Коэффициента ошибок, в библиотеке Comm Sinks
Установите Receive delay на 68.
Установите Output data на Port.
Проверяйте флажок Stop simulation.
Установите Target number of errors на 100.
Отобразитесь в библиотеке Simulink Sinks
Перетащите базовый край значка, чтобы сделать отображение достаточно большим для трех записей.
Соедините блоки как в фигуре. В окне модели выберите Simulation> Model Configuration parameters, чтобы открыть диалоговое окно Configuration Parameters. Установите Stop time на inf.
Примечания по Модели. Матричные аннотации размера появляются на соединительных линиях, только если вы кликаете по меню Display и выбираете Signals & Ports> Signal Dimensions. Энкодер принимает 2 1 вектор-столбец и производит вектор-столбец 3 на 1, в то время как декодер делает противоположное. Параметр Samples per frame в блоке Bernoulli Binary Generator равняется 2, потому что блок должен сгенерировать слово сообщения длины 2.
Параметр Receive delay в блоке Error Rate Calculation равняется 68, который является длиной вектора (2) из восстановленных времен сообщения значение Traceback depth (34) в блоке Viterbi Decoder. Если вы исследуете переданные и полученные сигналы как матрицы в рабочем пространстве MATLAB, вы видите, что первые 34 строки восстановленного сообщения состоят из нулей, в то время как последующие строки являются декодируемыми сообщениями. Таким образом задержка полученного сигнала является 34 векторами длины 2, или 68 выборок.
Выполнение модели производит, отображают вывод, состоящий из трех чисел: коэффициент ошибок, общее количество ошибок и общее количество сравнений, которые блок Error Rate Calculation делает во время симуляции. (Первые два числа отличаются в зависимости от ваших значений Initial seed по Бернуллиевому Бинарному Генератору и Бинарным Симметричным блокам Канала.) Остановки симуляции после 100 ошибок происходят, потому что Target number of errors установлен в 100 в блоке Error Rate Calculation. Коэффициент ошибок намного меньше, чем 0.02, Error probability в блоке Binary Symmetric Channel.
Этот пример обрабатывает проколотый сверточный код. Это начинается путем генерации 30 000 случайных битов и кодирования их использующий rate-3/4 сверточный энкодер с шаблоном прокола [1 1 1 0 0 1]. Итоговый вектор содержит 40 000 битов, которые сопоставлены со значениями-1 и 1 для передачи. Проколотый код, punctcode, проходит через аддитивный белый Гауссов шумовой канал. Затем vitdec декодирует шумный вектор с помощью типа решения 'unquant'.
Наконец, пример вычисляет частоту ошибок по битам и количество битовых ошибок.
len = 30000; msg = randi([0 1], len, 1); % Random data t = poly2trellis(7, [133 171]); % Define trellis. % Create a ConvolutionalEncoder System object hConvEnc = comm.ConvolutionalEncoder(t, ... 'PuncturePatternSource', 'Property', ... 'PuncturePattern', [1;1;1;0;0;1]); % Create an AWGNChannel System object. hChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)',... 'SNR', 3); % Create a ViterbiDecoder System object hVitDec = comm.ViterbiDecoder(t, 'InputFormat', 'Unquantized', ... 'TracebackDepth', 96, 'TerminationMethod', 'Truncated', ... 'PuncturePatternSource', 'Property', ... 'PuncturePattern', [1;1;1;0;0;1]); % Create a ErrorRate Calculator System object. hErrorCalc = comm.ErrorRate; berP = zeros(3,1); berPE = berP; % Store BER values punctcode = step(hConvEnc,msg); % Length is (2*len)*2/3. tcode = 1-2*punctcode; % Map "0" bit to 1 and "1" bit to -1 hChan.SignalPower = (tcode'*tcode)/length(tcode); ncode = step(hChan,tcode); % Add noise. % Decode the punctured code decoded = step(hVitDec,ncode); % Decode. berP = step(hErrorCalc, msg, decoded);% Bit error rate % Erase the least reliable 100 symbols, then decode release(hVitDec); reset(hErrorCalc) hVitDec.ErasuresInputPort = true; [dummy idx] = sort(abs(ncode)); erasures = zeros(size(ncode)); erasures(idx(1:100)) = 1; decoded = step(hVitDec,ncode, erasures); % Decode. berPE = step(hErrorCalc, msg, decoded);% Bit error rate fprintf('Number of errors with puncturing: %d\n', berP(2)) fprintf('Number of errors with puncturing and erasures: %d\n', berPE(2))
Этот раздел объясняет, как использовать блок Convolutional Encoder, чтобы реализовать систематический энкодер с обратной связью. Код систематичен, если фактические слова сообщения появляются как часть кодовых комбинаций. Следующая схема показывает пример систематического энкодера.
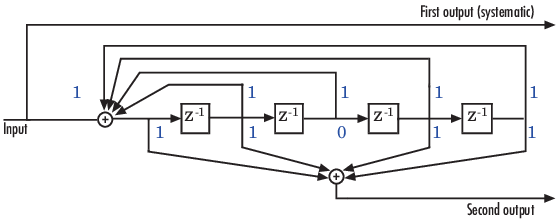
Чтобы реализовать этот энкодер, установите параметр Trellis structure в блоке Convolutional Encoder к poly2trellis(5, [37 33], 37). Эта установка соответствует
Продолжительность ограничения: 5
Пара полинома генератора: [37 33]
Полином обратной связи: 37
Полином обратной связи представлен бинарным вектором [1 1 1 1 1], соответствуя верхней строке двоичных цифр. Эти цифры указывают на связи от выходных параметров регистров к сумматору. Начальный 1 соответствует входному биту. Восьмеричное представление двоичного числа 11111 равняется 37.
Чтобы реализовать систематический код, установите первый полином генератора совпадать с полиномом обратной связи в параметре Trellis structure блока Convolutional Encoder. В этом примере оба полинома имеют восьмеричное представление 37.
Второй полином генератора представлен бинарным вектором [1 1 0 1 1], соответствуя более низкой строке двоичных цифр. Восьмеричное число, соответствующее двоичному числу 11011, равняется 33.
Для получения дополнительной информации об установке параметров маски для блока Convolutional Encoder см. Полиномиальное Описание Сверточного кода.
Этот пример создает уровень 1/2 сверточный код. Это использует квантизатор и блок Viterbi Decoder, чтобы выполнить декодирование мягкого решения. Это описание затрагивает эти темы:
Обзор Симуляции. Модель находится в следующей фигуре. Чтобы открыть модель, введите doc_softdecision в командной строке MATLAB. Симуляция создает случайный сигнал двоичного сообщения, кодирует сообщение в сверточный код, модулирует код с помощью метода бинарного манипулирования сдвига фазы (BPSK) и добавляет белый Гауссов шум в модулируемые данные в порядке моделировать шумный канал. Затем симуляция готовит полученные данные к блоку декодирования и декодирует. Наконец, симуляция сравнивает декодируемую информацию с сигналом исходного сообщения в порядке вычислить частоту ошибок по битам. Сверточный энкодер сконфигурирован как уровень 1/2 энкодер. Для каждых 2 битов энкодер добавляет еще 2 избыточных бита. Чтобы разместить это и добавить правильное количество шума, параметр Eb/No (dB) блока AWGN в действительности разделен на два путем вычитания 10*log10 (2). Концы симуляции после обработки 100 битовых ошибок или 107 битов сообщения, какой бы ни на первом месте.
Определение Сверточного кода. feedforward сверточный энкодер в этом примере изображен ниже.

Продолжительность ограничения энкодера является скаляром, поскольку энкодер имеет вход того. Значение продолжительности ограничения является количеством битов, сохраненных в сдвиговом регистре, включая текущий вход. Существует шесть регистров памяти, и текущий вход составляет один бит. Таким образом продолжительность ограничения кода равняется 7.
Генератор кода 1 2 матрица восьмеричных чисел, потому что энкодер имеет вход того и два выходных параметров. Первый элемент в матрице указывает, какие входные значения способствуют первому выводу, и второй элемент в матрице указывает, какие входные значения способствуют второму выводу.
Например, первый вывод в схеме энкодера является 2 суммами по модулю самого правого и четырьмя крайними левыми элементами в массиве схемы входных значений. Семиразрядное двоичное число 1111001 получает эту информацию и эквивалентно восьмеричному числу 171. Восьмеричное число 171 таким образом становится первой записью матрицы генератора кода. Здесь, каждый триплет битов использует крайний левый бит в качестве старшего значащего бита. Второй вывод соответствует двоичному числу 1011011, которое эквивалентно восьмеричному числу 133. Генератор кода поэтому [171 133].
Параметр Trellis structure в блоке Convolutional Encoder говорит блок который код использовать при обработке данных. В этом случае функция poly2trellis, в Communications Toolbox, преобразовывает продолжительность ограничения и пару восьмеричных чисел в допустимую структуру решетки.
В то время как данные о сообщении, вводящие блок Convolutional Encoder, являются скалярным потоком битов, закодированные данные, оставляя блок являются потоком бинарных векторов длины 2.
Отображение Полученных Данных. Полученные данные, то есть, вывод блока AWGN Channel, состоят из комплексных чисел, которые являются близко к-1 и 1. В порядке восстановить исходное двоичное сообщение, часть получателя модели должна декодировать сверточный код. Блок Viterbi Decoder в этой модели ожидает, что ее входные данные будут целыми числами между 0 и 7. Демодулятор, пользовательская подсистема в этой модели, преобразовывает полученные данные в формат, который блок Viterbi Decoder может интерпретировать правильно. А именно, подсистема демодулятора
Преобразовывает полученный сигнал данных в действительный сигнал путем удаления его мнимой части. Разумно принять, что мнимая часть полученных данных не содержит важную информацию, потому что мнимая часть передаваемых данных является нулем (игнорирование небольших ошибок округления) и потому что шум канала не очень мощен.
Нормирует полученные данные путем деления на стандартное отклонение шумовой оценки и затем умножения на-1.
Квантует нормированные данные с помощью трех битов.
Комбинация этого отображения и отображения решения блока Viterbi Decoder инвертирует модуляцию BPSK, которую блок BPSK Modulator Baseband выполняет на стороне передачи этой модели. Чтобы исследовать подсистему демодулятора более подробно, дважды кликните, значок маркировал Soft-Output BPSK Demodulator.
Декодирование Сверточного кода. После того, как полученные данные правильно сопоставлены с длиной 2 вектора 3-битных значений решения, блок Viterbi Decoder декодирует его. Блок использует мягкий алгоритм выбора решения с 23 различными входными значениями, потому что параметром Decision type является Soft Decision, и параметром Number of soft decision bits является 3.
Интерпретация мягкого решения данных
Когда параметр Decision type устанавливается на Soft Decision, блок Viterbi Decoder требует входных значений между 0 и 2b-1, где b является параметром Number of soft decision bits. Блок интерпретирует 0 как самое уверенное решение, что бит кодовой комбинации является 0 и интерпретирует 2b-1 как самое уверенное решение, что бит кодовой комбинации является 1. Значения, промежуточные эти экстремальные значения, представляют менее уверенные решения. В следующей таблице перечислены интерпретации восьми возможных входных значений для этого примера.
| Значение решения | Интерпретация |
|---|---|
| 0 | Самый уверенный 0 |
| 1 | Второй самый уверенный 0 |
| 2 | Третий самый большой уверенный 0 |
| 3 | Наименее уверенный 0 |
| 4 | Наименее уверенный 1 |
| 5 | Третий самый большой уверенный 1 |
| 6 | Второй самый уверенный 1 |
| 7 | Самый уверенный 1 |
Traceback и Decoding Delay
Параметр Traceback depth в блоке Viterbi Decoder представляет длину задержки декодирования. Типичные значения для traceback глубины являются приблизительно пять или шесть раз продолжительностью ограничения, которая была бы 35 или 42 в этом примере. Однако некоторые аппаратные реализации предлагают опции 48 и 96. Этот пример выбирает 48, потому что это ближе к целям (35, и 42), чем 96.
Задержка Полученных Данных. Receive delay parameterof блок Error Rate Calculation является ненулевым, потому что данный бит сообщения и его соответствующий восстановленный бит разделяются вовремя ненулевой суммой времени симуляции. Параметр Receive delay говорит блок который элементы его входных сигналов выдержать сравнение при проверке ошибок.
В этом случае Получить значение задержки равно значению глубины Traceback (48).
Сравнение Результатов симуляции с Теоретическими Результатами. В этом разделе описывается сравнить частоту ошибок по битам в этой симуляции с частотой ошибок по битам, которая теоретически следовала бы из неквантованного декодирования. Процесс включает несколько шагов, описанных в этих разделах:
Вычисление теоретических границ для частоты ошибок по битам
Чтобы вычислить теоретические границы для Свинца частоты ошибок по битам сверточного кода в этой модели, можно использовать эту оценку на основе декодирования неквантованного решения:
В этой оценке CD является суммой битовых ошибок для ошибочных событий расстояния d, и f является свободным расстоянием кода. Фунт количества является попарной вероятностью появления ошибки, данной
где R является уровнем кода 1/2, и erfc является MATLAB дополнительная функция ошибок, заданная
Значения для содействующего CD и свободного расстояния f находятся в опубликованных статьях, таких как Frenger, P., П. Ортен и Оттоссон, “Сверточные коды с Оптимальным Спектром Расстояния”, издание 3 IEEE Communications, стр 317-319, ноябрь 1999. Свободное расстояние для этого кода является f = 10.
Следующие команды вычисляют значения Свинца для значений Eb/N0 в диапазоне от 1 до 4 с шагом 0,5:
EbNoVec = [1:0.5:4.0]; R = 1/2; % Errs is the vector of sums of bit errors for % error events at distance d, for d from 10 to 29. Errs = [36 0 211 0 1404 0 11633 0 77433 0 502690 0,... 3322763 0 21292910 0 134365911 0 843425871 0]; % P is the matrix of pairwise error probilities, for % Eb/No values in EbNoVec and d from 10 to 29. P = zeros(20,7); % Initialize. for d = 10:29 P(d-9,:) = (1/2)*erfc(sqrt(d*R*10.^(EbNoVec/10))); end % Bounds is the vector of upper bounds for the bit error % rate, for Eb/No values in EbNoVec. Bounds = Errs*P;
Симуляция многократно, чтобы собрать частоты ошибок по битам
Можно эффективно отличаться параметры симуляции при помощи функции sim, чтобы запустить симуляцию из командной строки MATLAB. Например, следующий код вычисляет частоту ошибок по битам в отношениях энергии, подведенной к долоту к шуму в пределах от 1 дБ к 4 дБ с шагом 0,5 дБ. Это собирает все частоты ошибок по битам из этих симуляций в матричном BERVec. Это также строит частоты ошибок по битам в окне рисунка наряду с теоретическими границами, вычисленными в предыдущем фрагменте кода.
Сначала откройте модель путем нажатия здесь в Браузере документации MATLAB. Затем выполните эти команды, которые могут занять несколько минут.
% Plot theoretical bounds and set up figure. figure; semilogy(EbNoVec,Bounds,'bo',1,NaN,'r*'); xlabel('Eb/No (dB)'); ylabel('Bit Error Rate'); title('Bit Error Rate (BER)'); legend('Theoretical bound on BER','Actual BER'); axis([1 4 1e-5 1]); hold on; BERVec = []; % Make the noise level variable. set_param('doc_softdecision/AWGN Channel',... 'EsNodB','EbNodB+10*log10(1/2)'); % Simulate multiple times. for n = 1:length(EbNoVec) EbNodB = EbNoVec(n); sim('doc_softdecision',5000000); BERVec(n,:) = BER_Data; semilogy(EbNoVec(n),BERVec(n,1),'r*'); % Plot point. drawnow; end hold off;
Оценка для Свинца принимает, что декодер использует неквантованные данные, то есть, бесконечно прекрасное квантование. В отличие от этого, симуляция в этом примере использует 8-уровневое (3-битное) квантование. Из-за этого квантования моделируемая частота ошибок по битам является не совсем настолько же низкой как связанное, когда отношение сигнал-шум высоко.
График частоты ошибок по битам против отношения сигнал-шум следует. Местоположения ваших фактических точек BER могут отличаться, потому что симуляция включает случайные числа.

Этот пример демонстрирует Тэйлбитинга, кодирующего использование энкодеров обратной связи. Для энкодеров обратной связи конечное состояние зависит от целого блока данных. Чтобы выполнить tailbiting, необходимо вычислить для данного информационного вектора (битов N), начальное состояние, которое приводит к тому же конечному состоянию после того, как блок данных закодирован.
Это достигается на двух шагах:
Первый шаг должен определить ответ нулевого состояния для данного блока данных. Энкодер запускается во все-нулевом состоянии. Целый блок данных вводится, и выходные биты проигнорированы. После N биты, энкодер находится в XN состояния [zs]. От этого состояния мы вычисляем соответствующее начальное состояние X0 и инициализируем энкодер с X0.
Второй шаг является фактическим кодированием. Энкодер запускает с начального состояния X0, блок данных вводится, и допустимая кодовая комбинация выводится, который соответствует тому же условию государственной границы.
Обратитесь к [8] для теоретического вычисления начального состояния X0 от XN [zs] использующий формулировку пространства состояний. Это - одноразовое вычисление, которое зависит от длины блока и на практике могло быть реализовано как интерполяционная таблица. Здесь мы определяем эту таблицу отображения путем симуляции всех возможных записей для выбранной решетки и длины блока.
Чтобы открыть модель, введите doc_mtailbiting_wfeedback в командной строке MATLAB.
function mapStValues = getMapping(blkLen, trellis)
% The function returns the mapping value for the given block
length and trellis to be used for determining the initial
state from the zero-state response.
% All possible combinations of the mappings
mapStValuesTab = perms(0:trellis.numStates-1);
% Loop over all the combinations of the mapping entries:
for i = 1:length(mapStValuesTab)
mapStValues = mapStValuesTab(i,:);
% Model parameterized for the Block length
sim('mtailbiting_wfeedback');
% Check the boundary condition for each run
% if ending and starting states match, choose that mapping set
if unique(out)==0
return
end
endВыбор возвращенного mapStValues для параметра Table data блока Direct Lookup Table (n-D) в подсистеме Поиска выполнит tailbiting, кодирующий для выбранной длины блока и решетки.
[1] Кларк, Джордж К. Младший, и J. Затвор Каин, кодирование с коррекцией ошибок для цифровой связи, Нью-Йорка, нажатия пленума, 1981.
[2] Gitlin, Ричард Д., Иеремия Ф. Хейз, и Стивен Б. Вайнштейн, Дэта-Коммуникэйшнс-Принкиплс, Нью-Йорк, нажатие пленума, 1992.
[3] Frenger, P., П. Ортен и Т. Оттоссон, "Коды свертки с Оптимальным Спектром Расстояния", Коммуникационные Буквы IEEE, издание 3, стр 317-319, ноябрь 1999.
Циклическое, Хэмминг и типичная линейная функциональность блочного кода в этом продукте предлагают вам несколько способов организовать биты в сообщениях или кодовых комбинациях. Эти темы объясняют доступные форматы:
Используйте MATLAB, чтобы создать сообщения и кодовые комбинации в бинарном векторном формате
Используйте MATLAB, чтобы создать сообщения и кодовые комбинации в бинарном матричном формате
Используйте MATLAB, чтобы создать сообщения и кодовые комбинации в десятичном векторном формате
Чтобы изучить, как представлять слова для BCH или кодов Тростника-Solomon, смотрите, Представляют Слова для Кодов BCH или Представляют Слова для Кодов Тростника-Solomon.
Используйте MATLAB, чтобы Создать сообщения и Кодовые комбинации в Бинарном Векторном формате. Ваши сообщения и кодовые комбинации могут принять форму векторов, содержащих 0s и 1 с. Например, сообщения и коды могут быть похожими на msg и code в строках ниже.
n = 6; k = 4; % Set codeword length and message length % for a [6,4] code. msg = [1 0 0 1 1 0 1 0 1 0 1 1]'; % Message is a binary column. code = encode(msg,n,k,'cyclic'); % Code will be a binary column. msg' code'
Вывод ниже.
ans =
Columns 1 through 5
1 0 0 1 1
Columns 6 through 10
0 1 0 1 0
Columns 11 through 12
1 1
ans =
Columns 1 through 5
1 1 1 0 0
Columns 6 through 10
1 0 0 1 0
Columns 11 through 15
1 0 0 1 1
Columns 16 through 18
0 1 1 В этом примере msg состоит из 12 записей, которые интерпретированы, когда три 4-разрядных (потому что k = 4) обмениваются сообщениями. code итогового вектора включает три 6-разрядных (потому что n = 6) кодовые комбинации, которые конкатенированы, чтобы сформировать вектор из длины 18. Биты четности в начале каждой кодовой комбинации.
Используйте MATLAB, чтобы Создать сообщения и Кодовые комбинации в Бинарном Матричном Формате. Можно организовать информацию о кодировании, чтобы подчеркнуть группировку цифр в сообщения и кодовые комбинации. Если вы используете этот подход, каждое сообщение или кодовая комбинация занимают строку в бинарной матрице. Пример ниже иллюстрирует этот подход путем листинга каждого 4-битного сообщения на отличной строке в msg и каждой 6-битной кодовой комбинации на отличной строке в code.
n = 6; k = 4; % Set codeword length and message length. msg = [1 0 0 1; 1 0 1 0; 1 0 1 1]; % Message is a binary matrix. code = encode(msg,n,k,'cyclic'); % Code will be a binary matrix. msg code
Вывод ниже.
msg =
1 0 0 1
1 0 1 0
1 0 1 1
code =
1 1 1 0 0 1
0 0 1 0 1 0
0 1 1 0 1 1
В бинарном матричном формате матрица сообщения должна иметь столбцы k. Соответствующая матрица кода имеет столбцы n. Биты четности в начале каждой строки.
Используйте MATLAB, чтобы Создать сообщения и Кодовые комбинации в Десятичном Векторном формате. Ваши сообщения и кодовые комбинации могут принять форму векторов, содержащих целые числа. Каждый элемент вектора дает десятичное представление битов в одном сообщении или одной кодовой комбинации.
Если 2^n или 2^k являются очень большими, необходимо использовать двоичный формат по умолчанию вместо десятичного формата. Это вызвано тем, что функция использует двоичный формат внутренне, в то время как ошибка округления, сопоставленная с преобразованием многих битов к большим десятичным числам и назад, может быть существенной.
Когда вы будете использовать десятичный векторный формат, encode ожидает, что крайний левый бит будет младшим значащим битом.
Синтаксис для команды encode должен упомянуть десятичный формат явным образом, как в примере ниже. Заметьте, что /decimal добавлен к четвертому аргументу в команде encode.
n = 6; k = 4; % Set codeword length and message length. msg = [9;5;13]; % Message is a decimal column vector. % Code will be a decimal vector. code = encode(msg,n,k,'cyclic/decimal')
Вывод ниже.
code =
39
20
54
Эти три примера выше использовали циклическое кодирование. Форматы для сообщений и кодов подобны для Хэмминга и типичных линейных блочных кодов.
Этот подраздел описывает элементы, в которых вы можете нуждаться в порядке обработать [n, k] циклический, Хэмминг и типичные линейные блочные коды. Таблица ниже приводит элементы и методы кодирования, для которых они являются самыми важными.
Параметры, используемые в методах блочного кодирования
| Параметр | Метод блочного кодирования |
|---|---|
| Порождающая матрица | Типичный линейный блок |
| Матрица проверки четности | Типичный линейный блок |
| Полином генератора | Циклический |
| Декодирование таблицы | Типичный линейный блок, Хэмминг |
Порождающая матрица. Процесс кодирования сообщения в [n, k] линейный блочный код определяется k-by-n порождающей матрицей G. А именно, 1 вектором сообщения k v закодирован в вектор кодовой комбинации 1 на n vG. Если G имеет форму [Ик П] или [П Ик], где P является некоторым k-by-(n-k) матрица, и Ик является k-by-k единичной матрицей, G, как говорят, находится в стандартной форме. (Некоторые авторы, например, Кларк и Каин [2], используют первую стандартную форму, в то время как другие, например, Лин и Костелло [3], используют второе.) Большинство функций в этом тулбоксе принимает, что порождающая матрица находится в стандартной форме, когда вы используете его в качестве входного параметра.
Некоторые примеры матриц генератора находятся в следующем разделе, Матрице Проверки четности.
Матрица проверки четности. Декодируя [n, k] линейный блочный код требует (n-k)-by-n матрицы H проверки четности. GHtr = 0 (mod 2), удовлетворяет, где Htr обозначает, что матрица транспонирует H, G является порождающей матрицей кода, и эта нулевая матрица является k-by-(n-k). Если G = [Ик П] затем H = [-Ptr Чернила]. Большинство функций в этом продукте принимает, что матрица проверки четности находится в стандартной форме, когда вы используете его в качестве входного параметра.
Приведенная ниже таблица обобщает стандартные формы генератора и матриц проверки четности для [n, k] бинарный линейный блочный код.
| Тип матрицы | Стандартная форма | Размерности |
|---|---|---|
| Генератор | [Ик П] или [П Ик] | k-by-n |
| Проверка четности | [Чернила-P'] или [Чернила-P'] | (n-k)-by-n |
Ик является единичной матрицей размера k, и символ ' указывает, что матрица транспонирует. (Для двоичных кодов знаки "минус" в упомянутой выше форме проверки четности не важны; то есть,-1 = 1 в бинарном поле.)
Примеры
В команде ниже, parmat является матрицей проверки четности, и genmat является порождающей матрицей для Кода Хемминга в который [n, k] = [23-1, n-3] = [7,4]. genmat имеет стандартную форму [П Ик].
[parmat,genmat] = hammgen(3)
parmat =
1 0 0 1 0 1 1
0 1 0 1 1 1 0
0 0 1 0 1 1 1
genmat =
1 1 0 1 0 0 0
0 1 1 0 1 0 0
1 1 1 0 0 1 0
1 0 1 0 0 0 1
Следующий пример находит проверку четности и матрицы генератора для [7,3] циклический код. Функция cyclpoly упоминается ниже в Полиноме Генератора.
genpoly = cyclpoly(7,3);
[parmat,genmat] = cyclgen(7,genpoly)
parmat =
1 0 0 0 1 1 0
0 1 0 0 0 1 1
0 0 1 0 1 1 1
0 0 0 1 1 0 1
genmat =
1 0 1 1 1 0 0
1 1 1 0 0 1 0
0 1 1 1 0 0 1
Пример ниже преобразований порождающая матрица для [5,3] линейный блочный код в соответствующую матрицу проверки четности.
genmat = [1 0 0 1 0; 0 1 0 1 1; 0 0 1 0 1];
parmat = gen2par(genmat)
parmat =
1 1 0 1 0
0 1 1 0 1
Тот же функциональный gen2par может также преобразовать матрицу проверки четности в порождающую матрицу.
Полином генератора. Циклические коды имеют алгебраические свойства, которые позволяют полиному определять процесс кодирования полностью. Этот так называемый полином генератора является степенью - (n-k) делитель полинома xn-1. Линт фургона [5] объясняет, как полином генератора определяет циклический код.
Функция cyclpoly производит полиномы генератора для циклических кодов. cyclpoly представляет полином генератора использование вектора - строки, который перечисляет коэффициенты полинома в порядке возрастающих степеней переменной. Например, команда
genpoly = cyclpoly(7,3)
genpoly =
1 0 1 1 1
находит, что один допустимый полином генератора для [7,3] циклический код равняется 1 + x2 + x3 + x4.
Декодирование Таблицы. Таблица декодирования говорит декодер, как исправить ошибки, которые могут повредить код во время передачи. Коды Хемминга могут исправить любую односимвольную ошибку в любой кодовой комбинации. Другие коды могут исправить, или частично исправить, ошибки, которые повреждают больше чем один символ в данной кодовой комбинации.
Этот тулбокс представляет таблицу декодирования как матрицу со столбцами n и строками 2^(n-k). Каждая строка дает вектор исправления для одного полученного вектора кодовой комбинации. Таблица декодирования Хэмминга имеет n +1 строка. Функция syndtable генерирует таблицу декодирования для данной матрицы проверки четности.
Используйте таблицу декодирования в MATLAB
Скрипт ниже показов, как использовать таблицу декодирования Хэмминга, чтобы исправить ошибку в полученном сообщении. Функция hammgen производит матрицу проверки четности, в то время как функция syndtable производит таблицу декодирования. Транспонирование матрицы проверки четности умножается слева полученной кодовой комбинацией, приводя к синдрому. Таблица декодирования помогает определить вектор исправления. Исправленная кодовая комбинация является суммой (по модулю 2) вектора исправления и полученной кодовой комбинации.
% Use a [7,4] Hamming code. m = 3; n = 2^m-1; k = n-m; parmat = hammgen(m); % Produce parity-check matrix. trt = syndtable(parmat); % Produce decoding table. recd = [1 0 0 1 1 1 1] % Suppose this is the received vector. syndrome = rem(recd * parmat',2); syndrome_de = bi2de(syndrome,'left-msb'); % Convert to decimal. disp(['Syndrome = ',num2str(syndrome_de),... ' (decimal), ',num2str(syndrome),' (binary)']) corrvect = trt(1+syndrome_de,:) % Correction vector % Now compute the corrected codeword. correctedcode = rem(corrvect+recd,2)
Вывод ниже.
recd =
1 0 0 1 1 1 1
Syndrome = 3 (decimal), 0 1 1 (binary)
corrvect =
0 0 0 0 1 0 0
correctedcode =
1 0 0 1 0 1 1
Функциями для кодирования и декодирования циклического, Хэмминг и типичные линейные блочные коды является encode и decode. В этом разделе рассматриваются, как использовать эти функции, чтобы создать и декодировать типичные линейные блочные коды, циклические коды и Коды Хемминга.
Типичные Линейные Блочные коды. Кодирование сообщения с помощью типичного линейного блочного кода требует порождающей матрицы. Если вы задали переменные msg, n, k, и genmat, любую из команд
code = encode(msg,n,k,'linear',genmat); code = encode(msg,n,k,'linear/decimal',genmat);
кодирует информацию в msg с помощью [n, k] код, который определяет порождающая матрица genmat. Опция /decimal, подходящая, когда 2^n и 2^k не являются очень большими, указывает, что msg содержит неотрицательные десятичные целые числа, а не их бинарные представления. Смотрите Представляют Слова для Линейных Блочных кодов или страницу с описанием для encode для описания форматов msg и code.
Декодирование кода требует порождающей матрицы и возможно таблицы декодирования. Если вы задали переменные code, n, k, genmat, и возможно также trt, то команды
newmsg = decode(code,n,k,'linear',genmat); newmsg = decode(code,n,k,'linear/decimal',genmat); newmsg = decode(code,n,k,'linear',genmat,trt); newmsg = decode(code,n,k,'linear/decimal',genmat,trt);
декодируйте информацию в code, с помощью [n, k] код, который определяет порождающая матрица genmat. decode также исправляет ошибки согласно инструкциям в таблице декодирования, что trt представляет.
Пример: типичное линейное блочное кодирование
Пример ниже кодирует сообщение, искусственно добавляет некоторый шум, декодирует шумный код и отслеживает ошибки, которые декодер обнаруживает по пути. Поскольку таблица декодирования содержит только нули, декодер не исправляет ошибок.
n = 4; k = 2; genmat = [[1 1; 1 0], eye(2)]; % Generator matrix msg = [0 1; 0 0; 1 0]; % Three messages, two bits each % Create three codewords, four bits each. code = encode(msg,n,k,'linear',genmat); noisycode = rem(code + randerr(3,4,[0 1;.7 .3]),2); % Add noise. trt = zeros(2^(n-k),n); % No correction of errors % Decode, keeping track of all detected errors. [newmsg,err] = decode(noisycode,n,k,'linear',genmat,trt); err_words = find(err~=0) % Find out which words had errors.
Вывод указывает, что ошибки произошли в первых и вторых словах. Ваши результаты могут отличаться, потому что этот пример использует случайные числа в качестве ошибок.
err_words =
1
2
Циклические Коды. Циклический код является линейным блочным кодом со свойством, что циклические сдвиги кодовой комбинации (выраженный как ряд битов) являются также кодовыми комбинациями. Альтернативная характеристика циклических кодов основана на своем полиноме генератора, как упомянуто в Полиноме Генератора и обсудила в [5].
Кодирование сообщения с помощью циклического кода требует полинома генератора. Если вы задали переменные msg, n, k и genpoly, то любая из команд
code = encode(msg,n,k,'cyclic',genpoly); code = encode(msg,n,k,'cyclic/decimal',genpoly);
кодирует информацию в msg с помощью [n, k] код, определенный полиномом генератора genpoly. genpoly является дополнительным аргументом для encode. Полиномом генератора по умолчанию является cyclpoly(n,k). Опция /decimal, подходящая, когда 2^n и 2^k не являются очень большими, указывает, что msg содержит неотрицательные десятичные целые числа, а не их бинарные представления. Смотрите Представляют Слова для Линейных Блочных кодов или страницу с описанием для encode для описания форматов msg и code.
Декодирование кода требует полинома генератора и возможно таблицы декодирования. Если вы задали переменные code, n, k, genpoly и trt, то команды
newmsg = decode(code,n,k,'cyclic',genpoly); newmsg = decode(code,n,k,'cyclic/decimal',genpoly); newmsg = decode(code,n,k,'cyclic',genpoly,trt); newmsg = decode(code,n,k,'cyclic/decimal',genpoly,trt);
декодируйте информацию в code, с помощью [n, k] код, который определяет порождающая матрица genmat. decode также исправляет ошибки согласно инструкциям в таблице декодирования, что trt представляет. genpoly является дополнительным аргументом в первых двух синтаксисах выше. Полиномом генератора по умолчанию является cyclpoly(n,k).
Пример
Можно изменить пример в Типичных Линейных Блочных кодах так, чтобы он использовал циклический метод кодирования вместо линейного блочного кода с порождающей матрицей genmat. Делайте изменения описанными ниже:
Замените вторую строку
genpoly = [1 0 1]; % generator poly is 1 + x^2В пятых и девятых строках (encode и команды decode), замените genmat genpoly и замените 'linear' 'cyclic'.
Другой пример кодирования и декодирования циклического кода находится на странице с описанием для encode.
Коды Хемминга. Страницы с описанием для encode и decode содержат примеры кодирования и декодирования Кодов Хемминга. Кроме того, раздел Decoding Table иллюстрирует исправление ошибок в Коде Хемминга.
Этот пример показывает очень просто, как использовать энкодер и декодер. Это иллюстрирует соответствующие длины вектора сигналов кода и сообщения для кодеров. Поскольку блок Error Rate Calculation принимает только скаляры или основанные на кадре вектор-столбцы как переданные и полученные сигналы, этот пример использует основанные на кадре вектор-столбцы повсюду. (Это таким образом избегает необходимости изменять атрибуты сигнала с помощью блока, такие как Преобразование из 1D в 2D.)

Откройте эту модель путем ввода doc_hamming в командной строке MATLAB. Чтобы создать модель, соберите и сконфигурируйте эти блоки:
Бернуллиевый Бинарный Генератор, в библиотеке Comm Sources
Установите Probability of a zero на .5.
Установите Initial seed на любой положительный целочисленный скаляр, предпочтительно вывод функции randn.
Проверяйте флажок Frame-based outputs.
Установите Samples per frame на 4.
Энкодер Хэмминга, со значениями параметров по умолчанию
Декодер Хэмминга, со значениями параметров по умолчанию
Вычисление Коэффициента ошибок, в библиотеке Comm Sinks, со значениями параметров по умолчанию
Соедините блоки как в предыдущей фигуре. Кликните по меню Display и выберите Signals & Ports> Signal Dimensions. После обновления схемы при необходимости (Simulation> Update Diagram), строки коннектора показывают соответствующие атрибуты сигнала. Строки коннектора удваивают строки, чтобы указать на основанные на кадре сигналы, и аннотации рядом со строками показывают, что сигналы являются вектор-столбцами соответствующих размеров.
В этом разделе описывается уменьшать коэффициент ошибок путем добавления кода с коррекцией ошибок. Эти данные показывают модель, которая использует Код Хемминга.

Чтобы открыть полную версию модели, введите doc_hamming в посдказке MATLAB.
Создавание модели кода Хемминга
Можно создать модель Кода Хемминга путем выполнения этих шагов:
Введите doc_channel в посдказке MATLAB, чтобы открыть модель шума канала.
Затем сохраните модель как my_hamming в папке, где вы сохраняете свои рабочие файлы.
От Библиотеки Simulink Браузер перетаскивают блоки Декодера Энкодера и Хэмминга Хэмминга от подбиблиотеки Error Detection и Correction/Block в окно модели.
Кликните по правильной границе модели и перетащите его к праву расширить окно модели.
Переместите Бинарный Симметричный Канал, Вычисление Коэффициента ошибок и блоки Отображения направо путем перетаскивания.
Создайте достаточно пространства между Бернуллиевым Бинарным Генератором и Бинарными Симметричными блоками Канала, чтобы соответствовать Энкодеру Хэмминга между ними.
Перетащите блок Hamming Encoder сверху строки между блоком Bernoulli Binary Generator и блоком Binary Symmetric Channel, справа от точки разветвления, как показано в следующей фигуре. Затем отпустите кнопку мыши. Блок Hamming Encoder должен автоматически соединиться со строкой от блока Bernoulli Binary Generator до блока Binary Symmetric Channel.
Переместите блоки снова, чтобы создать достаточно пространства между Бинарным Симметричным Каналом и блоками Вычисления Коэффициента ошибок, чтобы соответствовать Декодеру Хэмминга между ними.
Перетащите блок Hamming Decoder сверху строки между блоком Binary Symmetric Channel и блоком Error Rate Calculation.
Модель должна теперь напомнить эту фигуру.

Используя блоки энкодера и декодера Хэмминга
Блок Hamming Encoder кодирует данные, прежде чем это будет отправлено через канал. Код по умолчанию [7,4] Код Хемминга, который кодирует слова сообщения длины 4 в кодовые комбинации длины 7. В результате блок преобразовывает кадры размера 4 в кадры размера 7. Код может исправить одну ошибку в каждой переданной кодовой комбинации.
Для [n, k] код, вход к блоку Hamming Encoder должен состоять из векторов размера k. В этом примере, k = 4.
Блок Hamming Decoder декодирует данные после того, как это будет отправлено через канал. Если самое большее одна ошибка создается в кодовой комбинации каналом, блок декодирует слово правильно. Однако, если больше чем одна ошибка происходит, блок Hamming Decoder может декодировать неправильно.
Чтобы узнать больше о функциях блочного кодирования, смотрите Блочные коды.
Установка параметров в модели кода Хемминга
Дважды кликните блок Bernoulli Binary Generator и внесите следующие изменения в установки параметров в диалоговом окне блока, как показано в следующей фигуре:
Установите Samples per frame на 4. Это преобразовывает вывод блока в кадры размера 4 в порядке удовлетворить входное требование Блока Энкодера Хэмминга. Смотрите Основанную на выборке и Основанную на кадре Обработку для получения дополнительной информации о кадрах.
Много блоков, таких как блок Hamming Encoder, требуют, чтобы их вход был вектором определенного размера. Если вы соединяете исходный блок, такой как блок Bernoulli Binary Generator, к одному из этих блоков, устанавливаете Samples per frame на необходимое значение. Для этой модели параметр Samples per frame блока Bernoulli Binary Generator должен быть кратным параметру Message Length K блока Hamming Encoder.
Маркировка блока отображения
Можно изменить метку, которая, кажется, ниже блока делает его более информативным. Например, чтобы изменить метку ниже блока Display к 'Error Rate Display', сначала выберите метку с мышью. Это заставляет поле появляться вокруг текста. Введите изменения в тексте в поле.
Выполнение модели кода Хемминга
Чтобы запустить модель, выберите Simulation > Start. Модель останавливается после того, как 100 ошибок происходят. Коэффициент ошибок, отображенный в главном окне блока Display, является приблизительно.001. Вы получаете немного отличающиеся результаты, если вы изменяете параметры Initial seed в модели или запускаете симуляцию в течение различного отрезка времени.
Вы ожидаете коэффициент ошибок приблизительно.001 по следующей причине: вероятность двух или больше ошибок, происходящих в кодовой комбинации длины 7,
1 – (0.99)7 – 7(0.99)6(0.01) = 0.002
Если кодовые комбинации с двумя или больше ошибками будут декодироваться случайным образом, вы ожидаете, что приблизительно половина битов в декодируемых словах сообщения будет неправильной. Это указывает, что.001 рыночная стоимость для частоты ошибок по битам.
Чтобы получить более низкий коэффициент ошибок для той же вероятности ошибки, попытайтесь использовать Код Хемминга с большими параметрами. Для этого измените параметры Codeword length и Message length в диалоговых окнах блока Decoder Энкодера и Хэмминга Хэмминга. Также необходимо внести соответствующие изменения в параметры блока Bernoulli Binary Generator и блока Binary Symmetric Channel.
Отображение форматов кадра
Можно отобразить размеры кадров данных в различных частях модели путем нажатия на меню Display и выбора Signals & Ports> Signal Dimensions. Строка, выводящая из блока Bernoulli Binary Generator, маркирована [4x1], указав, что его вывод состоит из вектор-столбцов размера 4. Поскольку блок Hamming Encoder использует [7,4] код, он преобразовывает кадры размера 4 в кадры размера 7, таким образом, его вывод маркирован [7x1].

Добавление осциллографа к модели
Чтобы отобразить ошибки канала, произведенные блоком Binary Symmetric Channel, добавьте блок Scope в модель. Это - хороший способ видеть, функционирует ли ваша модель правильно. Пример, показанный в следующей фигуре, показывает, где вставить блок Scope в модель.
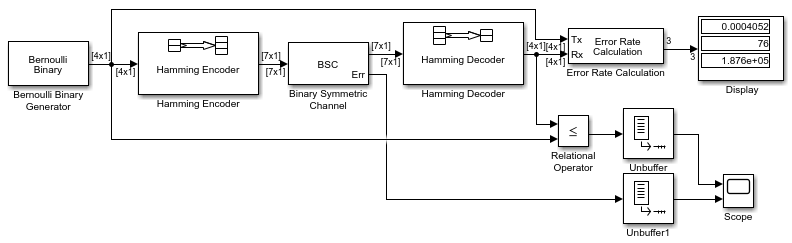
Чтобы создать эту модель от, один показанный в фигуре Уменьшает Коэффициент ошибок Используя Код Хемминга, выполняет эти шаги:
Перетащите следующие блоки от Браузера Библиотеки Simulink в окно модели:
Блок Relational Operator, от библиотеки Simulink Logic и Bit Operations
Блок Scope, от библиотеки Simulink Sinks
Две копии блока Unbuffer, от подбиблиотеки Buffers библиотеки Signal Management в DSP System Toolbox™
Дважды кликните блок Binary Symmetric Channel, чтобы открыть его диалоговое окно и выбрать Output error vector. Это создает второй выходной порт для блока, который несет вектор ошибок.
Дважды кликните блок Scope, под View > Configuration Properties ..., установите Number of input ports на 2. Выберите Layout и подсветите два блока вертикально. Нажмите OK.
Соедините блоки как показано в предыдущей фигуре.
Установка параметров в расширенной модели
Внесите следующие изменения в параметры для блоков, которые вы добавили в модель.
Блок Вычисления Коэффициента ошибок – Дважды кликает блок Error Rate Calculation и очищает поле рядом с Stop simulation в диалоговом окне блока.
Блок Scope – блок Scope отображает ошибки канала и неисправленные ошибки. Сконфигурировать блок,
Дважды кликните блок Scope, выберите 'View > Configuration Properties …'.
Выберите вкладку Time и установите Time span на 5000.
Выберите вкладку Logging и установите Limit data points to last на 30000.
Нажмите OK.
Осциллограф должен теперь появиться как показано.
Чтобы сконфигурировать оси, выполните эти шаги:
Щелкните правой кнопкой по вертикальной оси по левой стороне верхнего осциллографа.
В контекстном меню выберите Axes properties.
Установите Y-limits (Minimum) на -1.
Установите Y-limits (Maximum) на 2 и нажмите OK.
Повторите те же шаги для вертикальной оси более низкого осциллографа.
Расширьте окно scope, пока это не примерно в три раза более широко, чем это высоко. Можно сделать это путем нажатия на правильную границу окна и перетаскивания границы направо при нажатии левой кнопки мыши.
Оператор отношения – Набор Relational Operator к ~= в диалоговом окне блока. Блок Relational Operator сравнивает переданный сигнал, прибывающий из блока Bernoulli Random Generator, с полученным сигналом, прибывающим из блока Hamming Decoder. Блок выводит 0, когда два сигнала соглашаются и 1, когда они не соглашаются.
Наблюдение ошибок канала с осциллографом
Когда вы запускаете модель, осциллограф отображает ошибочные данные. В конце каждого 5 000 временных шагов осциллограф появляется как показано эта фигура. Осциллограф затем очищает отображенные данные и отображает следующие 5 000 точек данных.
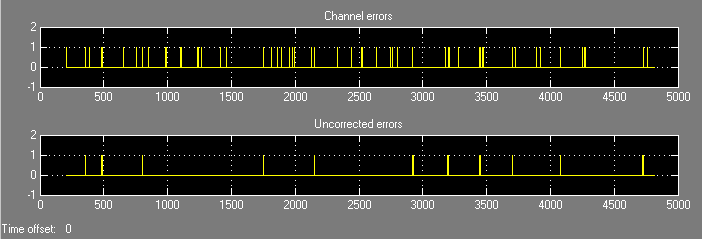
Верхний осциллограф показывает ошибки канала, сгенерированные блоком Binary Symmetric Channel. Более низкий осциллограф показывает ошибки, которые не исправляются кодированием канала.
Нажмите кнопку Stop на панели инструментов наверху окна модели, чтобы остановить осциллограф.
Вы видите отдельные ошибки путем увеличивания масштаб осциллографа. Сначала нажмите среднюю кнопку лупы, наверху оставленную окна Scope. Затем кликните по одной из строк в более низком осциллографе. Это увеличивает масштаб горизонтально на строке. Продолжите кликать по строкам в более низком осциллографе, пока горизонтальный масштаб не будет достаточно прекрасен, чтобы обнаружить отдельные ошибки. Типичный пример того, что вы можете видеть, показывают в фигуре ниже.
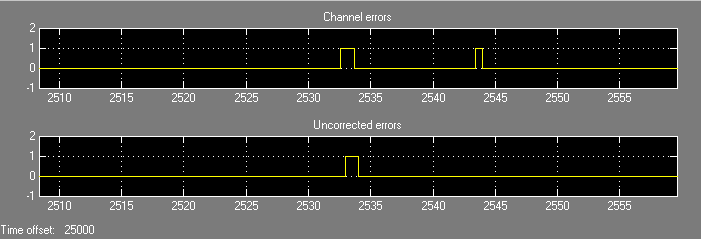
Более широкий меандр посреди верхнего осциллографа представляет два 1 с. Эти две ошибки, которые происходят в одной кодовой комбинации, не исправляются. Это составляет неисправленные ошибки в более низком осциллографе. Более узкий меандр справа от верхнего осциллографа представляет одну ошибку, которая исправляется.
Когда вы будете сделаны, наблюдая ошибки, выберите Simulation > Stop.
Экспортируйте Данные в MATLAB, объясняет, как отправить ошибочные данные в рабочее пространство MATLAB для более детального анализа.
Сообщение для [n, k] кодом BCH должен быть k - двоичный массив Поля Галуа столбца. Кодом, который соответствует тому сообщению, является n - двоичный массив Поля Галуа столбца. Каждая строка этих массивов Поля Галуа представляет одно слово.
Пример ниже иллюстрирует, как представлять слова для [15, 11] код BCH.
h = comm.BCHEncoder
msg = [1 0 0 1 0; 1 0 1 1 1]; % Messages in a Galois array
obj = comm.BCHEncoder;
c1 = step(obj, msg(1,:)');
c2 = step(obj, msg(2,:)');
cbch = [c1 c2].'Вывод
Columns 1 through 5
1 0 0 1 0
1 0 1 1 1
Columns 6 through 10
0 0 1 1 1
0 0 0 0 1
Columns 11 through 15
1 0 1 0 1
0 1 0 0 1 Коды BCH используют специальные значения n и k:
n, длина кодовой комбинации, является целым числом формы 2m-1 для некоторого целочисленного m> 2.
k, длина сообщения, является положительным целым числом меньше, чем n. Однако только некоторые положительные целые числа меньше, чем n являются допустимым выбором для k. Смотрите страницу с описанием блока BCH Encoder для списка некоторых допустимых значений k, соответствующего значениям n до 511.
BCH Encoder и Системные объекты BCH Decoder создают и декодируют коды BCH, использование данных, описанных в, Представляет Слова для Кодов BCH и Параметры для Кодов BCH.
Темы
Пример: BCH Кодирование Синтаксисов. Пример ниже иллюстрирует, как закодировать и декодировать данные с помощью [15, 5] код BCH.
n = 15; k = 5; % Codeword length and message length msg = randi([0 1],4*k,1); % Four random binary messages % Simplest syntax for encoding enc = comm.BCHEncoder(n,k); dec = comm.BCHDecoder(n,k); c1 = step(enc,msg); % BCH encoding d1 = step(dec,c1); % BCH decoding % Check that the decoding worked correctly. chk = isequal(d1,msg) % The following code shows how to perform the encoding and decoding % operations if one chooses to prepend the parity symbols. % Steps for converting encoded data with appended parity symbols % to encoded data with prepended parity symbols c11 = reshape(c1, n, []); c12 = circshift(c11,n-k); c1_prepend = c12(:); % BCH encoded data with prepended parity symbols % Steps for converting encoded data with prepended parity symbols % to encoded data with appended parity symbols prior to decoding c21 = reshape(c1_prepend, n, []); c22 = circshift(c21,k); c1_append = c22(:); % BCH encoded data with appended parity symbols % Check that the prepend-to-append conversion worked correctly. d1_append = step(dec,c1_append); chk = isequal(msg,d1_append)
Вывод ниже.
chk =
1
Обнаружьте и Исправьте Ошибки в Коде BCH Используя MATLAB. Следующий пример иллюстрирует результаты декодирования для поврежденного кода. Пример кодирует некоторые данные, вводит ошибки в каждой кодовой комбинации и пытается декодировать шумный код с помощью Системного объекта BCH Decoder.
n = 15; k = 5; % Codeword length and message length [gp,t] = bchgenpoly(n,k); % t is error-correction capability. nw = 4; % Number of words to process msgw = randi([0 1], nw*k, 1); % Random k-symbol messages enc = comm.BCHEncoder(n,k,gp); dec = comm.BCHDecoder(n,k,gp); c = step(enc, msgw); % Encode the data. noise = randerr(nw,n,t); % t errors per codeword noisy = noise'; noisy = noisy(:); cnoisy = mod(c + noisy,2); % Add noise to the code. [dc, nerrs] = step(dec, cnoisy); % Decode cnoisy. % Check that the decoding worked correctly. chk2 = isequal(dc,msgw) nerrs % Find out how many errors have been corrected.
Заметьте, что массив шумовых значений содержит двоичные значения, и что операция сложения , c + noise происходит в GF Поля Галуа (2), потому что c является массивом Поля Галуа в GF (2).
Вывод от примера ниже. Ненулевое значение ans указывает, что декодер смог исправить поврежденные кодовые комбинации и восстановить исходное сообщение. Значения в векторном nerrs указывают, что декодер исправил ошибки t в каждой кодовой комбинации.
chk2 =
1
nerrs =
3
3
3
3Чрезмерный шум в кодовых комбинациях BCH
В предыдущем примере Системный объект BCH Decoder исправил все ошибки. Однако каждый код BCH имеет конечную возможность исправления ошибок. Чтобы узнать больше, как Системный объект BCH Decoder ведет себя, когда шум является чрезмерным, смотрите аналогичное обсуждение для кодов Тростника-Solomon в Чрезмерном Шуме в Кодовых комбинациях Тростника-Solomon.
Обзор. Алгоритм декодирования только для ошибок, используемый для BCH и кодов RS, может быть описан следующими шагами (разделяет 5.3.2, 5.4, и 5.6 в [2]).
Вычислите первое 2t условия бесконечного полинома синдрома степени, .
Если те 2t условия все равны 0, затем код не имеет никаких ошибок, никакое исправление не должно быть выполнено, и концы алгоритма декодирования.
Если одно или несколько условий являются ненулевыми, вычисляют ошибочный полином локатора, Λ (z), с помощью алгоритма Berlekamp.
Вычислите ошибочный полином средства анализа, , через
Исправьте ошибку в кодовой комбинации согласно
где ошибочное значение в положение th в кодовой комбинации, m является значением меньше, чем поддержка с коррекцией ошибок кода, ошибочный полином значения, Λ '(z) формальная производная [5] из ошибочного полинома локатора, Λ (z), и α является примитивным элементом Поля Галуа кода.
Дальнейшее описание нескольких из шагов дано в следующих разделах.
Вычисление синдрома. Для кодов узкого смысла, 2t условия вычисляются путем оценки полученной кодовой комбинации в последовательных степенях α (примитивный элемент поля) от 0 до 2t-1. Другими словами, если мы принимаем индексацию на основе одну кодовых комбинаций и полином синдрома , и это кодовые комбинации имеет форму , затем каждый термин из дан как
Ошибочное Вычисление Полинома Локатора. Ошибочный полином локатора, Λ (z), найден с помощью алгоритма Berlekamp. Полное описание этого алгоритма найдено в [2], но мы обобщаем алгоритм можно следующим образом.
Мы задаем следующие переменные.
| Переменная | Описание |
|---|---|
| n | Переменная Iterator |
| k | Переменная Iterator |
| L | Длина регистра обратной связи раньше генерировала первое 2t условия |
| D (z) | Полином исправления |
| d | Несоответствие |
Следующая схема показывает, что итеративная процедура (т.е. алгоритм Berlekamp) раньше находила Λ (z).
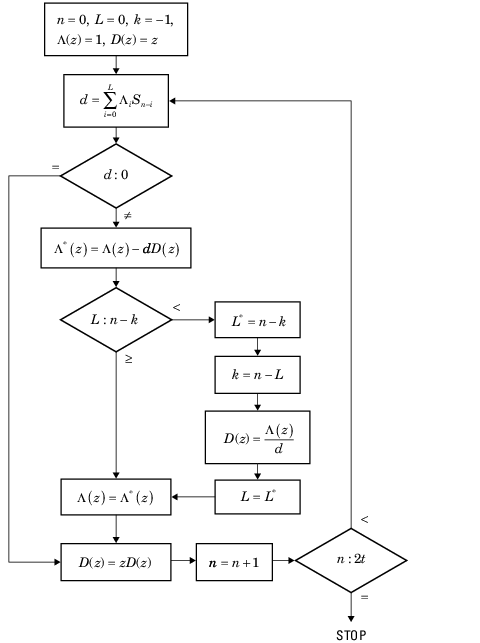
Ошибочное Вычисление Полинома Средства анализа. Ошибочный полином средства анализа, , просто свертка Λ (z) и .
Этот тулбокс поддерживает коды Тростника-Solomon, которые используют символы Мбит вместо битов. Сообщение для [n, k] кодом Тростника-Solomon должен быть k - массив Поля Галуа столбца в поле GF (2m). Каждая запись массива должна быть целым числом между 0 и 2m-1. Кодом, соответствующим тому сообщению, является n - массив Поля Галуа столбца в GF (2 м). Длина кодовой комбинации n должна быть между 3 и 2m-1.
Для получения информации о массивах Поля Галуа и как создать их, смотрите Элементы Представления Полей Галуа или страницы с описанием для функции gf.
Пример ниже иллюстрирует, как представлять слова для [7,3] код Тростника-Solomon.
n = 7; k = 3; % Codeword length and message length m = 3; % Number of bits in each symbol msg = [1 6 4; 0 4 3]; % Message is a Galois array. obj = comm.RSEncoder(n, k); c1 = step(obj, msg(1,:)'); c2 = step(obj, msg(2,:)'); c = [c1 c2].'
Вывод
C =
1 6 4 4 3 6 3
0 4 3 3 7 4 7
В этом разделе описываются несколько целых чисел, связанных с кодами Тростника-Solomon, и обсуждает, как найти полиномы генератора.
Допустимые Значения Целочисленных Параметров. Приведенная ниже таблица обобщает значения и допустимые значения некоторых положительных целочисленных количеств, связанных с кодами Тростника-Solomon, как поддержано в этом тулбоксе. Количества n и k являются входными параметрами для функций Тростника-Solomon в этом тулбоксе.
| Символ | Значение | Значение или область значений |
|---|---|---|
| m | Количество битов на символ | Целое число между 3 и 16 |
n | Количество символов на кодовую комбинацию | Целое число между 3 и 2m-1 |
k | Количество символов на сообщение | Положительные целочисленные меньше, чем n, такой, что n-k ровен |
| t | Поддержка исправления ошибок кода | (n-k)/2 |
Полином генератора. Функция rsgenpoly производит полиномы генератора для кодов Тростника-Solomon. rsgenpoly представляет полином генератора использование вектора - строки Галуа, который перечисляет коэффициенты полинома в порядке убывающих степеней переменной. Если каждый символ имеет m биты, вектор - строка Галуа находится в поле GF (2m). Например, команда
r = rsgenpoly(15,13)
r = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
1 6 8
находит, что один полином генератора для [15,13] код Тростника-Solomon является X2 + (A2 + A) X + (A3), где A является корнем примитивного полинома по умолчанию для GF (16).
Алгебраическое выражение для полиномов генератора
Полиномы генератора, которые производит rsgenpoly, имеют форму (X - Ab) (X - Ab+1)... (X - Ab+2t-1), где b является целым числом, A является корнем примитивного полинома для Поля Галуа, и t является (n-k)/2. Значение по умолчанию b равняется 1. Вывод от rsgenpoly является результатом умножения факторов и сбора как степени X. Пример ниже проверяет эту формулу на случай [15,13] код Тростника-Solomon, с помощью b = 1.
n = 15; a = gf(2,log2(n+1)); % Root of primitive polynomial f1 = [1 a]; f2 = [1 a^2]; % Factors that form generator polynomial f = conv(f1,f2) % Generator polynomial, same as r above.
RS Encoder и Системные объекты RS Decoder создают и декодируют коды Тростника-Solomon, использование данных, описанных в, Представляет Слова для Кодов Тростника-Solomon и Параметры для Кодов Тростника-Solomon.
Этот раздел иллюстрирует, как использовать Системные объекты RS Decoder и RS Encoder. Темы
Синтаксисы Кодирования тростника-Solomon в MATLAB. Пример ниже иллюстрирует несколько способов закодировать и декодировать данные с помощью [15,13] код Тростника-Solomon. Пример показывает, что вы можете
Отличайтесь полином генератора для кода, с помощью rsgenpoly, чтобы произвести различный полином генератора.
Отличайтесь примитивный полином для Поля Галуа, которое содержит символы, с помощью входного параметра в gf.
Отличайтесь положение символов четности в кодовых комбинациях, выбирая или конец (значение по умолчанию) или начало.
Этот пример также показывает, что соответствующие синтаксисы RS Encoder и Системных объектов RS Decoder используют те же входные параметры, за исключением первого входного параметра.
m = 4; % Number of bits in each symbol n = 2^m-1; k = 13; % Codeword length and message length msg = randi([0 m-1],4*k,1); % Four random integer messages % Simplest syntax for encoding hEnc = comm.RSEncoder(n,k); hDec = comm.RSDecoder(n,k); c1 = step(hEnc, msg); d1 = step(hDec, c1); % Vary the generator polynomial for the code. release(hEnc), release(hDec) hEnc.GeneratorPolynomialSource = 'Property'; hDec.GeneratorPolynomialSource = 'Property'; hEnc.GeneratorPolynomial = rsgenpoly(n,k,19,2); hDec.GeneratorPolynomial = rsgenpoly(n,k,19,2); c2 = step(hEnc, msg); d2 = step(hDec, c2); % Vary the primitive polynomial for GF(16). release(hEnc), release(hDec) hEnc.PrimitivePolynomialSource = 'Property'; hDec.PrimitivePolynomialSource = 'Property'; hEnc.GeneratorPolynomialSource = 'Auto'; hDec.GeneratorPolynomialSource = 'Auto'; hEnc.PrimitivePolynomial = [1 1 0 0 1]; hDec.PrimitivePolynomial = [1 1 0 0 1]; c3 = step(hEnc, msg); d3 = step(hDec, c3); % Check that the decoding worked correctly. chk = isequal(d1,msg) & isequal(d2,msg) & isequal(d3,msg) % The following code shows how to perform the encoding and decoding % operations if one chooses to prepend the parity symbols. % Steps for converting encoded data with appended parity symbols % to encoded data with prepended parity symbols c31 = reshape(c3, n, []); c32 = circshift(c31,n-k); c3_prepend = c32(:); % RS encoded data with prepended parity symbols % Steps for converting encoded data with prepended parity symbols % to encoded data with appended parity symbols prior to decoding c34 = reshape(c3_prepend, n, []); c35 = circshift(c34,k); c3_append = c35(:); % RS encoded data with appended parity symbols % Check that the prepend-to-append conversion worked correctly. d3_append = step(hDec,c3_append); chk = isequal(msg,d3_append)
Вывод
chk =
1
Обнаружьте и Исправьте Ошибки в Коде Тростника-Solomon Используя MATLAB. Пример ниже иллюстрирует результаты декодирования для поврежденного кода. Пример кодирует некоторые данные, вводит ошибки в каждой кодовой комбинации и пытается декодировать шумный код с помощью Системного объекта RS Decoder.
m = 3; % Number of bits per symbol n = 2^m-1; k = 3; % Codeword length and message length t = (n-k)/2; % Error-correction capability of the code nw = 4; % Number of words to process msgw = randi([0 n],nw*k,1); % Random k-symbol messages hEnc = comm.RSEncoder(n,k); hDec = comm.RSDecoder(n,k); c = step(hEnc, msgw); % Encode the data. noise = (1+randi([0 n-1],nw,n)).*randerr(nw,n,t); % t errors per codeword noisy = noise'; noisy = noisy(:); cnoisy = gf(c,m) + noisy; % Add noise to the code under gf(m) arithmetic. [dc nerrs] = step(hDec, cnoisy.x); % Decode the noisy code. % Check that the decoding worked correctly. isequal(dc,msgw) nerrs % Find out how many errors hDec corrected.
Массив шумовых значений содержит целые числа между 1 и 2^m и операция сложения , c + noise происходит в GF Поля Галуа (2^m), потому что c является массивом Поля Галуа в GF (2^m).
Вывод от примера ниже. Ненулевое значение ans указывает, что декодер смог исправить поврежденные кодовые комбинации и восстановить исходное сообщение. Значения в векторном nerrs указывают, что декодер исправил ошибки t в каждой кодовой комбинации.
ans =
1
nerrs =
2
2
2
2
Чрезмерный Шум в Кодовых комбинациях Тростника-Solomon. В предыдущем примере Системный объект RS Encoder исправил все ошибки. Однако каждый код Тростника-Solomon имеет конечную возможность исправления ошибок. Если шум является столь большим, что поврежденная кодовая комбинация слишком далека в Расстоянии Хемминга от правильной кодовой комбинации, которая означает также
Поврежденная кодовая комбинация близко к допустимой кодовой комбинации кроме правильной кодовой комбинации. Декодер возвращает сообщение, которое соответствует другой кодовой комбинации.
Поврежденная кодовая комбинация не достаточно близка ни к какой кодовой комбинации для успешного декодирования. Эта ситуация называется отказом декодирования. Декодер удаляет символы в положениях четности от поврежденной кодовой комбинации и возвращает оставшиеся символы.
В обоих случаях декодер возвращает неправильное сообщение. Однако можно сказать, когда отказ декодирования происходит, потому что Системный объект RS Decoder также возвращает значение -1 в его втором выводе.
Чтобы исследовать случаи, в которых кодовые комбинации являются слишком шумными для успешного декодирования, измените предыдущий пример так, чтобы определение noise было
noise = (1+randi([0 n-1],nw,n)).*randerr(nw,n,t+1); % t+1 errors/rowСоздайте Сокращенные Коды Тростника-Solomon. Каждый энкодер Тростника-Solomon использует длину кодовой комбинации, которая равняется 2m-1 для целого числа m. Сокращенный код Тростника-Solomon - тот, в котором длина кодовой комбинации не является 2m-1. Сокращенный [n, k] код Тростника-Solomon неявно использует [n1, k1] энкодер, где
n1 = 2 м - 1, где m является количеством битов на символ
k1 = k + (n1 - n)
Поддержки Системного объекта RS Encoder сократили коды с помощью тех же синтаксисов, которые это использует для несокращенных кодов. Вы не должны указывать явным образом, что хотите использовать сокращенный код.
hEnc = comm.RSEncoder(7,5); ordinarycode = step(hEnc,[1 1 1 1 1]'); hEnc = comm.RSEncoder(5,3); shortenedcode = step(hEnc,[1 1 1 ]');
Как системный объект RS Encoder создает сокращенный код
При создании сокращенного кода Системный объект RS Encoder выполняет эти шаги:
Клавиатуры каждое сообщение преднезаконченными нулями
Кодирует каждое заполненное сообщение с помощью энкодера Тростника-Solomon, имеющего допустимую длину кодовой комбинации и желаемую возможность исправления ошибок
Удаляет дополнительные нули из символов нечетности каждой кодовой комбинации
Следующий пример иллюстрирует этот процесс.
n = 12; k = 8; % Lengths for the shortened code m = ceil(log2(n+1)); % Number of bits per symbol msg = randi([0 2^m-1],3*k,1); % Random array of 3 k-symbol words hEnc = comm.RSEncoder(n,k); code = step(hEnc, msg); % Create a shortened code. % Do the shortening manually, just to show how it works. n_pad = 2^m-1; % Codeword length in the actual encoder k_pad = k+(n_pad-n); % Messageword length in the actual encoder hEnc = comm.RSEncoder(n_pad,k_pad); mw = reshape(msg,k,[]); % Each column vector represents a messageword msg_pad = [zeros(n_pad-n,3); mw]; % Prepend zeros to each word. msg_pad = msg_pad(:); code_pad = step(hEnc,msg_pad); % Encode padded words. cw = reshape(code_pad,2^m-1,[]); % Each column vector represents a codeword code_eqv = cw(n_pad-n+1:n_pad,:); % Remove extra zeros. code_eqv = code_eqv(:); ck = isequal(code_eqv,code); % Returns true (1).
Чтобы найти полином генератора для циклического, BCH или код Тростника-Solomon, используют cyclpoly, bchgenpoly или функцию rsgenpoly, соответственно. Команды
genpolyCyclic = cyclpoly(15,5) % 1+X^5+X^10 genpolyBCH = bchgenpoly(15,5) % x^10+x^8+x^5+x^4+x^2+x+1 genpolyRS = rsgenpoly(15,5)
найдите полиномы генератора для блочных кодов различных типов. Вывод ниже.
genpolyCyclic =
1 0 0 0 0 1 0 0 0 0 1
genpolyBCH = GF(2) array.
Array elements =
1 0 1 0 0 1 1 0 1 1 1
genpolyRS = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
1 4 8 10 12 9 4 2 12 2 7
Форматы этих выходных параметров отличаются:
cyclpoly представляет полином генератора использование целочисленного вектора - строки, который перечисляет коэффициенты полинома в порядке возрастающих степеней переменной.
bchgenpoly и rsgenpoly представляют полином генератора использование вектора - строки Галуа, который перечисляет коэффициенты полинома в порядке убывающих степеней переменной.
rsgenpoly использует коэффициенты в Поле Галуа кроме бинарного поля GF (2). Для получения дополнительной информации о значении этих коэффициентов смотрите, Как Целые числа Соответствуют Элементам Поля Галуа и Полиномам по Полям Галуа.
Групповой из Полиномов Генератора. Некоторые пары длины сообщения и длины кодовой комбинации исключительно не определяют полином генератора. Синтаксисы для функций в примере выше также включают опции для получения полиномов генератора, которые удовлетворяют определенные ограничения, которые вы задаете. Смотрите страницы с описанием функций для получения дополнительной информации об опциях синтаксиса.
Алгебраическое выражение для Полиномов Генератора. Полиномы генератора, произведенные bchgenpoly и rsgenpoly, имеют форму (X - Ab) (X - Ab+1)... (X - Ab+2t-1), где A является примитивным элементом для соответствующего Поля Галуа, и b и t, целые числа. Смотрите страницы с описанием функций для получения дополнительной информации об этом выражении.
В этом разделе, представительном примере Рида Соломона, кодирующего с сокращением, прокалывание и стирания создаются с увеличивающейся сложностью исправления ошибок.
Пример энкодера с Сокращением и Прокалыванием. Следующие данные показывают представительный пример (7,3) энкодер Рида Соломона с сокращением и прокалыванием.
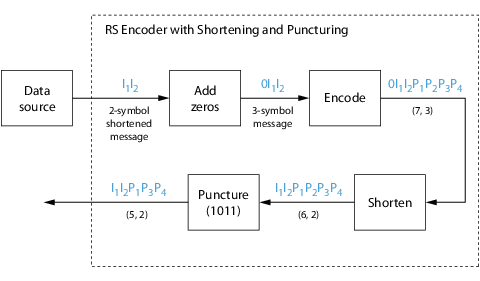
В этой фигуре, источник сообщения выходные параметры два информационных символа, определяемые I1I2. (Для примера BCH символы являются просто битами.), Поскольку код является сокращенным (7,3) код, нуль должен быть добавлен перед информационными символами, приведя к сообщению с тремя символами 0I1I2. Измененной последовательностью сообщения является затем RS, закодированный, и добавленный информационный нуль впоследствии удален, который приводит к результату I1I2P1P2P3P4. (В этом примере биты четности в конце кодовой комбинации.)
Операцией прокалывания управляет вектор прокола, который, в этом случае, является 1011. В векторе прокола 1 означает, что символ сохранен, и 0 средние значения, что символ выброшен. В этом примере операция прокалывания удаляет второй символ четности, приводя к итоговому вектору I1I2P1P3P4.
Пример декодера с Сокращением и Прокалыванием. Следующие данные показывают, как энкодер RS работает с сокращенной и проколотой кодовой комбинацией.
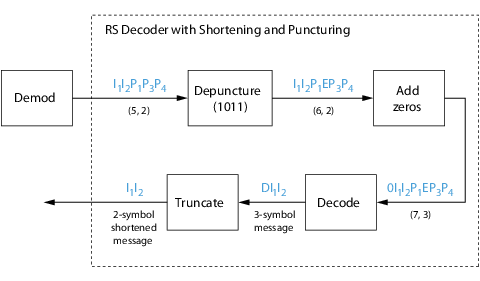
Этот случай соответствует работе энкодера, показанной в фигуре энкодера RS с сокращением и прокалыванием. Как показано в предыдущей фигуре, энкодер получает (5,2) кодовая комбинация, потому что это было сокращено от (7,3) кодовая комбинация одним символом, и один символ был также проколот.
Как первый шаг, декодер добавляет стирание, определяемое E, во втором положении четности кодовой комбинации. Это соответствует вектору прокола 1011. Добавление нуля составляет сокращение, таким же образом как показано в предыдущей фигуре. Одно стирание не превышает исправляющую стирание поддержку кода, который может исправить четыре стирания. Операция декодирования приводит к сообщению DI1I2 с тремя символами. Первый символ является усеченным, как в предыдущей фигуре, приводя к окончательному результату I1I2.
Пример энкодера с Сокращением, Прокалыванием и Стираниями. Следующие данные показывают декодер, работающий с проколотой, сокращенной кодовой комбинацией, также исправляя стирания, сгенерированные получателем.
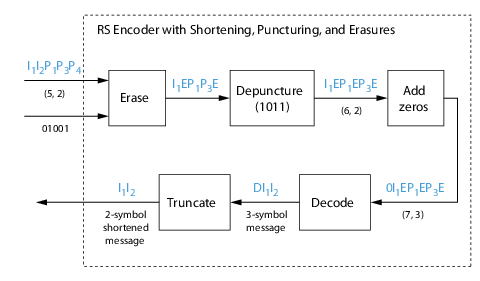
В этой фигуре демодулятор получает вектор I1I2P1P3P4 что отправленный энкодер. Демодулятор объявляет, что два из пяти полученных символов достаточно ненадежны, чтобы быть стертыми, такие, что символы 2 и 5, как считают, являются стираниями. 01 001 вектор, обеспеченный внешним источником, указывает на эти стирания. В векторе стираний 1 означает, что символ должен быть заменен символом стирания и 0 средние значения, что символ передается неизменный.
Блоки декодера получают кодовую комбинацию и вектор стирания, и выполняют стирания, обозначенные вектором 01001. В векторе стираний 1 означает, что символ должен быть заменен символом стирания и 0 средние значения, что символ передается неизменный. Получившийся вектор кодовой комбинации является I1EP1P3E, где E является символом стирания.
Кодовая комбинация затем depunctured, согласно вектору прокола, используемому в операции кодирования (т.е. 1011). Таким образом символ стирания вставляется между P1 и P3, приводя к вектору кодовой комбинации I1EP1EP3E.
Только до декодирования, сложение нулей в начале информационного вектора составляет сокращение. Итоговый вектор является 0I1EP1EP3E, таким, что (7,3) кодовая комбинация отправляется в алгоритм Berlekamp.
Эта кодовая комбинация декодируется, приводя к сообщению с тремя символами DI1I2 (где D относится к фиктивному символу). Наконец, удаление символа D от вектора сообщения составляет сокращение и приводит к исходному I1I2 вектору.
Для получения дополнительной информации смотрите, что Тростник-Solomon Кодирует со Стираниями, Проколами, и Сокращает пример.
Коды Имеющей малую плотность проверки четности (LDPC) являются кодами системы управления линейной погрешности с:
Разреженные матрицы проверки четности
Длины длинного блока, которые могут достигнуть производительности около предела Шеннона (см. Энкодер LDPC и Декодер LDPC),
Communications Toolbox выполняет LDPC, Кодирующий использование объекты MATLAB и блоки Simulink.
Процесс декодирования сделан итеративно. Если количество итераций является слишком маленьким, алгоритм не может сходиться. Вы, возможно, должны экспериментировать с количеством итераций, чтобы найти соответствующее значение для вашей модели. Для получения дополнительной информации на алгоритме декодирования, см. Алгоритм Декодирования.
В отличие от некоторых других кодеков, вы не можете соединить декодер LDPC непосредственно с выводом энкодера LDPC, потому что декодер требует логарифмических отношений правдоподобия (LLR). Таким образом можно использовать демодулятор, чтобы вычислить LLRs.

Кроме того, различающиеся другие декодеры, это возможно (несмотря на то, что редкий), что вывод декодера LDPC не удовлетворяет все проверки четности.
Поле Галуа является алгебраическим полем, которое имеет конечное число участников. Поля Галуа, имеющие участников на 2 м, используются в кодировании контроля ошибок и обозначаются GF (2 м). В этой главе описываются, как работать с полями, которые имеют участников на 2 м, где m является целым числом между 1 и 16. Разделы в этой главе следующие.
Если необходимо использовать Поля Галуа, имеющие нечетное число элементов, смотрите Поля Галуа Нечетной Характеристики.
Для получения дополнительной информации об определенных функциях, что массивы процесса элементов Поля Галуа, смотрите онлайновые страницы с описанием в документации для MATLAB или для программного обеспечения Communications Toolbox.
Обратите внимание на то, что объекты Поля Галуа не поддерживают метод copy.
Функции MATLAB, обобщение которых к Полям Галуа является прямым, чтобы описать, не имеют страниц с описанием в этом руководстве, потому что записи были бы идентичны тем в документации MATLAB.
Обсуждение Полей Галуа в этом документе использует несколько терминов, которые последовательно не используются в литературе. Определения, принятые здесь, появляются в Линте фургона [4]:
Примитивный элемент GF (2 м) является циклическим генератором группы ненулевых элементов GF (2 м). Это означает, что каждый ненулевой элемент поля может быть выражен как примитивный элемент, возведенный к некоторой целочисленной степени.
Примитивный полином для GF (2 м) является минимальным полиномом некоторого примитивного элемента GF (2 м). Это - полином бинарного коэффициента наименьшей ненулевой степени, имеющей определенный примитивный элемент как корень в GF (2 м). Как следствие примитивный полином имеет степень m и неприводим.
Определения подразумевают, что примитивный элемент является корнем соответствующего примитивного полинома.
Разделите Обзор. В этом разделе описывается создать массив Поля Галуа, который является выражением MATLAB, которое представляет элементы Поля Галуа. Этот раздел также описывает, как MATLAB, техническое вычислительное программное обеспечение интерпретирует числа, которые вы используете в представлении, и включает несколько примеров.
Создание массива Поля Галуа. Чтобы начать работать с данными из GF Поля Галуа (2^m), необходимо установить контекст путем соединения данных с важной информацией о поле. Функция gf выполняет эту ассоциацию и создает массив Поля Галуа в MATLAB. Эта функция принимает как входные параметры
Данные о Поле Галуа, x, который является массивом MATLAB, элементы которого являются целыми числами между 0 и 2^m-1.
(Необязательно) целое число, m, который указывает на x, находится в поле GF (2^m). Допустимые значения m между 1 и 16. Значение по умолчанию равняется 1, что означает, что поле является GF (2).
(Необязательно) положительное целое число, которое указывает, какой примитивный полином для GF (2^m) вы используете в представлениях в x. Если вы не используете этот входной параметр, gf использует примитивный полином по умолчанию для GF (2^m). Для получения информации об этом аргументе смотрите Определение Примитивного Полинома.
Вывод функции gf является переменной, которую MATLAB распознает массивом Поля Галуа, а не массивом целых чисел. В результате, когда вы управляете переменной, MATLAB работает в Поле Галуа, которое вы задали. Например, если вы применяете функцию log к массиву Поля Галуа, MATLAB вычисляет логарифм в Поле Галуа а не в области вещественных или комплексных чисел.
Когда MATLAB Неявно Создает массив Поля Галуа
Некоторые операции на массивах Поля Галуа требуют нескольких аргументов. Если вы задаете один аргумент, который является массивом Поля Галуа и другим, который является обычным массивом MATLAB, MATLAB интерпретирует обоих как массивы Поля Галуа в том же поле. Это неявно вызывает функцию gf на обычный массив MATLAB. Этот неявный вызов упрощает ваш синтаксис, потому что можно не использовать некоторые ссылки на функцию gf. Для примера упрощения смотрите Пример: Сложение и Вычитание.
Пример: Создание Переменных Поля Галуа. Код ниже создает вектор - строку, записи которого находятся в поле GF (4), и затем добавляет строку в себя.
x = 0:3; % A row vector containing integers m = 2; % Work in the field GF(2^2), or, GF(4). a = gf(x,m) % Create a Galois array in GF(2^m). b = a + a % Add a to itself, creating b.
Вывод
a = GF(2^2) array. Primitive polynomial = D^2+D+1 (7 decimal)
Array elements =
0 1 2 3
b = GF(2^2) array. Primitive polynomial = D^2+D+1 (7 decimal)
Array elements =
0 0 0 0
Вывод показывает значения массивов Поля Галуа под названием a и b. Каждый выходной раздел указывает
Поле, содержащее переменную, а именно, GF (2^2) = GF (4).
Примитивный полином для поля. В этом случае это - примитивный полином тулбокса по умолчанию для GF (4).
Массив значений Поля Галуа, которые содержит переменная. В частности, элементы массива в a являются точно элементами векторного x, и элементы массива в b являются четырьмя экземплярами нулевого элемента в GF (4).
Команда, которая создает b, показывает, как, задав переменную a как массив Поля Галуа, можно добавить a в себя при помощи обычного оператора +. MATLAB выполняет векторизованную операцию сложения в поле GF (4). Вывод показывает это
По сравнению с a b находится в том же поле и использует тот же примитивный полином. Не необходимо указать на поле при определении суммы, b, потому что MATLAB помнит что информация из определения слагаемых, a.
Элементы массива b являются нулями, потому что сумма любого значения с собой, в Поле Галуа характеристических двух, является нулем. Этот результат отличается от суммы x + x, который представляет операцию сложения в бесконечном поле целых чисел.
Пример: Представление Элементов GF (8). Проиллюстрировать то, что элементы массива в среднем значении Поля Галуа массивов, таблица ниже приводит элементы поля GF (8) как целые числа и как полиномы в примитивном элементе, A. Таблица должна помочь вам интерпретировать массив Поля Галуа как
gf8 = gf([0:7],3); % Galois vector in GF(2^3)
| Целочисленное представление | Бинарное представление | Элемент GF (8) |
|---|---|---|
| 0 | 000 | 0 |
| 1 | 001 | 1 |
| 2 | 010 | A |
| 3 | 011 | + 1 |
| 4 | 100 | A2 |
| 5 | 101 | A2 + 1 |
| 6 | 110 | A2 + A |
| 7 | 111 | A2 + + 1 |
Как Целые числа Соответствуют Элементам Поля Галуа. Основываясь на GF (8) пример выше, этот раздел объясняет интерпретацию элементов массива в массиве Поля Галуа в большей общности. Поле GF (2^m) имеет 2^m отличные элементы, которые этот тулбокс маркирует как 0, 1, 2..., 2^m-1. Эти целочисленные метки соответствуют элементам Поля Галуа через многочленное выражение, включающее примитивный элемент поля. А именно, каждое целое число между 0 и 2^m-1 имеет бинарное представление в битах m. Используя биты в бинарном представлении, когда коэффициенты в полиноме, где младший значащий бит является постоянным термином, приводят к бинарному полиному, порядок которого в большей части m-1. Оценка бинарного полинома в примитивном элементе GF (2^m) приводит к элементу поля.
С другой стороны любой элемент GF (2^m) может быть выражен как бинарный полином порядка в большей части m-1, оцененном в примитивном элементе поля. m - кортеж коэффициентов полинома соответствует бинарному представлению целого числа между 0 и 2^m.
Ниже символьный рисунок соответствия целочисленного X, представимого в двоичной форме, с элементом Поля Галуа. Каждый b k является или нулем или один, в то время как A является примитивным элементом.
Пример: Представление Примитивного Элемента. Код ниже задает переменную alph, которая представляет примитивный элемент поля GF (24).
m = 4; % Or choose any positive integer value of m. alph = gf(2,m) % Primitive element in GF(2^m)
Вывод
alph = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
2
Массив Поля Галуа alph представляет примитивный элемент из-за соответствия среди
Целое число 2, заданный в синтаксисе gf
Бинарное представление 2, который равняется 10 (или 0010 использований четыре бита)
Полином + 0, где A является примитивным элементом в этом поле (или 0A3 + 0A2 + + 0 использований четырех самых низких степеней A)
Примитивные Полиномы и Представления Элемента. Этот раздел основывается на обсуждении в Создании массива Поля Галуа путем описания, как задать собственный примитивный полином, когда вы создаете массив Поля Галуа. Темы
Если вы выполняете много вычислений с помощью примитивного полинома не по умолчанию, смотрите Скорость и Примитивные Полиномы Не по умолчанию.
Обсуждение в том, Как Целые числа Соответствуют Элементам Поля Галуа, обращается к примитивному элементу, который является корнем примитивного полинома поля. Когда вы используете функцию gf, чтобы создать массив Поля Галуа, функция интерпретирует целые числа в массиве относительно определенного примитивного полинома по умолчанию для того поля, если вы явным образом не обеспечиваете различный примитивный полином. Список примитивных полиномов по умолчанию находится на странице с описанием для функции gf.
Чтобы задать ваш собственный примитивный полином при создании массива Поля Галуа, используйте синтаксис как
c = gf(5,4,25) % 25 indicates the primitive polynomial for GF(16).вместо
c1= gf(5,4); % Use default primitive polynomial for GF(16).Дополнительный входной параметр, 25 в этом случае, задает примитивный полином для поля GF (2^m), в некотором роде подобный представлению, описанному в том, Как Целые числа Соответствуют Элементам Поля Галуа. В этом случае целое число 25 соответствует бинарному представлению 11 001, который в свою очередь соответствует полиномиальному D4 + D3 + 1.
Когда вы задаете примитивный полином, входной параметр должен иметь бинарное представление, использующее точно биты m+1, не включая ненужные начальные нули. Другими словами, примитивный полином для GF (2^m) всегда имеет, заказывают m.
Когда вы используете входной параметр, чтобы задать примитивный полином, вывод отражает ваш выбор путем показа целочисленного значения, а также полиномиального представления.
d = gf([1 2 3],4,25)
d = GF(2^4) array. Primitive polynomial = D^4+D^3+1 (25 decimal)
Array elements =
1 2 3После того, как вы задали массив Поля Галуа, вы не можете изменить примитивный полином, относительно которого MATLAB интерпретирует элементы массива.
Нахождение примитивных полиномов
Можно использовать функцию primpoly, чтобы найти, что примитивные полиномы для GF (2^m) и функция isprimitive определяют, примитивен ли полином для GF (2^m). Код ниже иллюстрирует.
m = 4; defaultprimpoly = primpoly(m) % Default primitive poly for GF(16) allprimpolys = primpoly(m,'all') % All primitive polys for GF(16) i1 = isprimitive(25) % Can 25 be the prim_poly input in gf(...)? i2 = isprimitive(21) % Can 21 be the prim_poly input in gf(...)?
Вывод ниже.
Primitive polynomial(s) =
D^4+D^1+1
defaultprimpoly =
19
Primitive polynomial(s) =
D^4+D^1+1
D^4+D^3+1
allprimpolys =
19
25
i1 =
1
i2 =
0
Эффект примитивных полиномов не по умолчанию на числовых результатах
Большинство полей предлагает разнообразный выбор для примитивного полинома, который помогает задать представление членов поля. Когда вы используете функцию gf, изменение примитивного полинома изменяет интерпретацию элементов массива и, в свою очередь, изменяет результаты некоторых последующих операций на массиве Поля Галуа. Например, возведение в степень примитивного элемента облегчает, чтобы видеть, как примитивный полином влияет на представления полевых элементов.
a11 = gf(2,3); % Use default primitive polynomial of 11. a13 = gf(2,3,13); % Use D^3+D^2+1 as the primitive polynomial. z = a13.^3 + a13.^2 + 1 % 0 because a13 satisfies the equation nz = a11.^3 + a11.^2 + 1 % Nonzero. a11 does not satisfy equation.
Вывод ниже показов, что, когда примитивный полином имеет целочисленное представление 13, массив Поля Галуа удовлетворяет определенному уравнению. В отличие от этого, когда примитивный полином имеет целочисленное представление 11, массиву Поля Галуа не удается удовлетворить уравнению.
z = GF(2^3) array. Primitive polynomial = D^3+D^2+1 (13 decimal)
Array elements =
0
nz = GF(2^3) array. Primitive polynomial = D^3+D+1 (11 decimal)
Array elements =
6
Вывод, когда вы пробуете этот пример, может также включать предупреждение об интерполяционных таблицах. Это нормально, если вы не использовали функцию gftable, чтобы оптимизировать вычисления, включающие примитивный полином не по умолчанию 13.
Разделите Обзор. Можно выполнить арифметические операции на массивах Поля Галуа при помощи знакомых операторов MATLAB, перечисленных в таблице ниже. Каждый раз, когда вы работаете с парой массивов Поля Галуа, оба массива должны быть в том же Поле Галуа.
| Операция | Оператор |
|---|---|
| Сложение | +
|
| Вычитание | -
|
| Поэлементное умножение | .*
|
| Умножение матриц | *
|
| Поэлементно оставленный деление | ./
|
| Поэлементное правильное деление | .\
|
| Матрица покинула деление | /
|
| Матричное правильное деление | \
|
| Поэлементное возведение в степень | .^
|
| Поэлементный логарифм | log()
|
| Возведение в степень квадрата матрица Галуа скалярным целым числом | ^
|
Для умножения и деления полиномов по Полю Галуа, смотрите Сложение и Вычитание Полиномов.
Пример: Сложение и Вычитание. Код ниже добавляет два массива Поля Галуа, чтобы составить таблицу сложения для GF (8). Сложение использует обычный оператор +. Код ниже также показывает, как индексировать в массив addtb, чтобы найти результат добавления 1 к элементам GF (8).
m = 3; e = repmat([0:2^m-1],2^m,1); f = gf(e,m); % Create a Galois array. addtb = f + f' % Add f to its own matrix transpose. addone = addtb(2,:); % Assign 2nd row to the Galois vector addone.
Вывод ниже.
addtb = GF(2^3) array. Primitive polynomial = D^3+D+1 (11 decimal)
Array elements =
0 1 2 3 4 5 6 7
1 0 3 2 5 4 7 6
2 3 0 1 6 7 4 5
3 2 1 0 7 6 5 4
4 5 6 7 0 1 2 3
5 4 7 6 1 0 3 2
6 7 4 5 2 3 0 1
7 6 5 4 3 2 1 0
Как пример чтения этой таблицы сложения, (7,4) запись в массиве addtb показывает, что gf(6,3) плюс gf(3,3) равняется gf(5,3). Эквивалентно, элемент A2+A плюс элемент A+1 равняется элементу A2+1. Эквивалентность является результатом бинарного представления 6 как 110, 3 как 011, и 5 как 101.
Таблица вычитания, которую можно получить, заменив + -, совпадает с addtb. Это вызвано тем, что вычитание и сложение являются идентичными операциями в поле характеристических двух. На самом деле нули по основной диагонали addtb иллюстрируют этот факт для GF (8).
Упрощение синтаксиса
Код ниже иллюстрирует скалярное расширение и неявное создание массива Поля Галуа от обычного массива MATLAB. h Поля Галуа массивов и h1 идентичны, но создание h использует более простой синтаксис.
g = gf(ones(2,3),4); % Create a Galois array explicitly. h = g + 5; % Add gf(5,4) to each element of g. h1 = g + gf(5*ones(2,3),4) % Same as h.
Вывод ниже.
h1 = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
4 4 4
4 4 4
Заметьте, что 1+5 сообщается как 4 в Поле Галуа. Это верно, потому что эти 5 представляют многочленное выражение, A2+1, и 1 + (A2+1) в GF (16) является A2. Кроме того, целое число, которое представляет многочленное выражение A2, равняется 4.
Пример: Умножение. Пример ниже умножает отдельные элементы в массиве Поля Галуа с помощью оператора .*. Это затем выполняет умножение матриц с помощью оператора *. Поэлементное умножение производит массив чьи соответствия размера те из входных параметров. В отличие от этого, умножение матриц производит скаляр Галуа, потому что это - матричное произведение вектора - строки с вектор-столбцом.
m = 5; row1 = gf([1:2:9],m); row2 = gf([2:2:10],m); col = row2'; % Transpose to create a column array. ep = row1 .* row2; % Elementwise product. mp = row1 * col; % Matrix product.
Таблица умножения для GF (8)
Как другой пример, код ниже умножает два вектора Галуа с помощью умножения матриц. Результатом является таблица умножения для GF (8).
m = 3;
els = gf([0:2^m-1]',m);
multb = els * els' % Multiply els by its own matrix transpose.Вывод ниже.
multb = GF(2^3) array. Primitive polynomial = D^3+D+1 (11 decimal)
Array elements =
0 0 0 0 0 0 0 0
0 1 2 3 4 5 6 7
0 2 4 6 3 1 7 5
0 3 6 5 7 4 1 2
0 4 3 7 6 2 5 1
0 5 1 4 2 7 3 6
0 6 7 1 5 3 2 4
0 7 5 2 1 6 4 3
Пример: Деление. Примеры ниже иллюстрируют эти четыре оператора деления в Поле Галуа путем вычисления мультипликативных инверсий отдельных элементов и массива. Можно также вычислить инверсии с помощью inv или с помощью возведения в степень-1.
Поэлементное деление
Этот пример делится 1 на каждый из отдельных элементов в массиве Поля Галуа с помощью операторов .\ и ./. Эти два оператора отличаются только по своей последовательности входных параметров. Каждый вектор частного перечисляет мультипликативные инверсии ненулевых элементов поля. В этом примере MATLAB расширяет скаляр 1 до размера nz перед вычислением; альтернативно, можно использовать в качестве аргументов два массива, одного размера.
m = 5; nz = gf([1:2^m-1],m); % Nonzero elements of the field inv1 = 1 ./ nz; % Divide 1 by each element. inv2 = nz .\ 1; % Obtain same result using .\ operator.
Матричное деление
Этот пример делит единичный массив на квадратный массив Поля Галуа mat с помощью операторов \ и /. Каждая матрица частного является мультипликативной инверсией mat. Заметьте, как оператор операции транспонирования (') появляется в эквивалентной операции с помощью \. Для квадратных матриц последовательность транспонирует операции, является ненужным, но для неквадратных матриц, это необходимо.
m = 5; mat = gf([1 2 3; 4 5 6; 7 8 9],m); minv1 = eye(3) / mat; % Compute matrix inverse. minv2 = (mat' \ eye(3)')'; % Obtain same result using \ operator.
Пример: Возведение в степень. Примеры ниже иллюстрируют, как вычислить целочисленные степени массива Поля Галуа. Чтобы выполнить матричное возведение в степень на массиве Поля Галуа, необходимо использовать квадратный массив Поля Галуа в качестве основы и дежурного блюда (не Галуа) целочисленный скаляр как экспонента.
Поэлементное возведение в степень
Этот пример вычисляет степени примитивного элемента, A, Поля Галуа. Это затем использует эти отдельно вычисленные степени оценить примитивный полином по умолчанию в A. Ответ нуля показывает, что A является корнем примитивного полинома. Оператор .^ exponentiates каждый элемент массива независимо.
m = 3; av = gf(2*ones(1,m+1),m); % Row containing primitive element expa = av .^ [0:m]; % Raise element to different powers. evp = expa(4)+expa(2)+expa(1) % Evaluate D^3 + D + 1.
Вывод ниже.
evp = GF(2^3) array. Primitive polynomial = D^3+D+1 (11 decimal)
Array elements =
0
Матричное возведение в степень
Этот пример вычисляет инверсию квадратной матрицы путем повышения матрицы до степени-1. Это также повышает квадратную матрицу до степеней 2 и-2.
m = 5; mat = gf([1 2 3; 4 5 6; 7 8 9],m); minvs = mat ^ (-1); % Matrix inverse matsq = mat^2; % Same as mat * mat matinvssq = mat^(-2); % Same as minvs * minvs
Пример: Поэлементный Логарифм. Код ниже вычисляет логарифм элементов массива Поля Галуа. Вывод указывает, как выразить каждый ненулевой элемент GF (8) как степень примитивного элемента. Логарифм нулевого элемента поля не определен.
gf8_nonzero = gf([1:7],3); % Vector of nonzero elements of GF(8) expformat = log(gf8_nonzero) % Logarithm of each element
Вывод
expformat =
0 1 3 2 6 4 5
Как пример того, как интерпретировать вывод, рассмотрите последнюю запись в каждом векторе в этом примере. Можно вывести, что элемент gf(7,3) в GF (8) может быть выражен как также
A5, с помощью последнего элемента expformat
A2+A+1, с помощью бинарного представления 7 как 111. Смотрите Пример: Представление Элементов GF (8) для получения дополнительной информации.
Разделите Обзор. Можно применить логические тесты к массивам Поля Галуа и получить логический массив. Некоторые важные типы тестов тестируют на равенство двух массивов Поля Галуа и тестируют на ненулевые значения в массиве Поля Галуа.
Тестирование на Равенство. Чтобы сравнить соответствующие элементы двух массивов Поля Галуа, которые имеют тот же размер, используйте операторы == и ~=. Результатом является логический массив, каждый элемент которого указывает на истину или ошибочность соответствующего поэлементного сравнения. Если вы используете те же операторы, чтобы сравнить скаляр с массивом Поля Галуа, MATLAB, техническое вычислительное программное обеспечение сравнивает скаляр с каждым элементом массива, производя логический массив, одного размера.
m = 5; r1 = gf([1:3],m); r2 = 1 ./ r1; lg1 = (r1 .* r2 == [1 1 1]) % Does each element equal one? lg2 = (r1 .* r2 == 1) % Same as above, using scalar expansion lg3 = (r1 ~= r2) % Does each element differ from its inverse?
Вывод ниже.
lg1 =
1 1 1
lg2 =
1 1 1
lg3 =
0 1 1
Сравнение isequal и ==
Чтобы сравнить целые массивы и получить логический скалярный результат, а не логический массив, используйте встроенную функцию isequal. Однако isequal использует строгие правила для своего сравнения и возвращает значение 0, (FALSE), если вы выдерживаете сравнение
Массив Поля Галуа с обычным массивом MATLAB, даже если значения соответствия элементов основного массива
Скаляр с нескалярным массивом, даже если все элементы в массиве совпадают со скаляром
Пример ниже иллюстрирует это различие между == и isequal.
m = 5; r1 = gf([1:3],m); r2 = 1 ./ r1; lg4 = isequal(r1 .* r2, [1 1 1]); % False lg5 = isequal(r1 .* r2, gf(1,m)); % False lg6 = isequal(r1 .* r2, gf([1 1 1],m)); % True
Тестирование на Ненулевые значения. Чтобы протестировать на ненулевые значения в векторе Галуа, или в столбцах массива Поля Галуа, который имеет больше чем одну строку, используют функция all или any. Эти две функции ведут себя точно так же, как обычные функции MATLAB any и all, за исключением того, что они рассматривают только элементы основного массива при игнорировании информации, о котором Поле Галуа элементы находятся в. Примеры ниже.
m = 3; randels = gf(randi([0 2^m-1],6,1),m); if all(randels) % If all elements are invertible invels = randels .\ 1; % Compute inverses of elements. else disp('At least one element was not invertible.'); end alph = gf(2,4); poly = 1 + alph + alph^3; if any(poly) % If poly contains a nonzero value disp('alph is not a root of 1 + D + D^3.'); end code = [0:4 4 0; 3:7 4 5] if all(code,2) % Is each row entirely nonzero? disp('Both codewords are entirely nonzero.'); else disp('At least one codeword contains a zero.'); end
Основные Манипуляции Массивов Поля Галуа. Основные операции над массивами на массивах Поля Галуа находятся в приведенной ниже таблице. Функциональность этих операций походит на операции MATLAB, имеющие тот же синтаксис.
| Операция | Синтаксис |
|---|---|
| Индексируйте в массив, возможно с помощью оператора двоеточия вместо вектора явных индексов | a(vector) или a(vector,vector1), где vector и/или vector1 может быть ":" вместо вектора |
| Транспонируйте массив | a'
|
| Конкатенируйте матрицы | [a,b] или [a;b]
|
| Создайте массив, указывавший диагональные элементы | diag(vector) или diag(vector,k)
|
| Извлеките диагональные элементы | diag(a) или diag(a,k)
|
| Извлеките нижнюю треугольную часть | tril(a) или tril(a,k)
|
| Извлеките верхнюю треугольную часть | triu(a) или triu(a,k)
|
| Измените форму массива | reshape(a,k1,k2)
|
Код ниже использует некоторые из этих синтаксисов.
m = 4; a = gf([0:15],m); a(1:2) = [13 13]; % Replace some elements of the vector a. b = reshape(a,2,8); % Create 2-by-8 matrix. c = [b([1 1 2],1:3); a(4:6)]; % Create 4-by-3 matrix. d = [c, a(1:4)']; % Create 4-by-4 matrix. dvec = diag(d); % Extract main diagonal of d. dmat = diag(a(5:9)); % Create 5-by-5 diagonal matrix dtril = tril(d); % Extract upper and lower triangular dtriu = triu(d); % parts of d.
Основная информация О Массивах Поля Галуа. Можно определить длину вектора Галуа или размер любого массива Поля Галуа с помощью функций size и length. Функциональность для массивов Поля Галуа походит на функциональность операций MATLAB на обычных массивах, за исключением того, что выходными аргументами от size и length всегда являются целые числа, не массивы Поля Галуа. Код ниже иллюстрирует использование этих функций.
m = 4; e = gf([0:5],m); f = reshape(e,2,3); lne = length(e); % Vector length of e szf = size(f); % Size of f, returned as a two-element row [nr,nc] = size(f); % Size of f, returned as two scalars nc2 = size(f,2); % Another way to compute number of columns
Положения ненулевых элементов
Другой тип информации, которую вы можете хотеть определить от массива Поля Галуа, является положениями ненулевых элементов. Для обычного массива MATLAB вы можете использовать функцию find. Однако для массива Поля Галуа, необходимо использовать find в сочетании с оператором ~=, как проиллюстрировано.
x = [0 1 2 1 0 2]; m = 2; g = gf(x,m); nzx = find(x); % Find nonzero values in the ordinary array x. nzg = find(g~=0); % Find nonzero values in the Galois array g.
Инвертирование Матриц и Вычисление Детерминантов. Чтобы инвертировать квадратный массив Поля Галуа, используйте функцию inv. Связанный функция det, которая вычисляет детерминант массива Поля Галуа. И inv и det ведут себя как их обычные дубликаты MATLAB, за исключением того, что они выполняют вычисления в Поле Галуа вместо в области комплексных чисел.
Массив Поля Галуа сингулярен, если и только если его детерминант является точно нулевым. Не необходимо рассмотреть ошибки округления, как в случае действительных и комплексных массивов.
Код ниже иллюстрирует матричную инверсию и определяющее вычисление.
m = 4; randommatrix = gf(randi([0 2^m-1],4,4),m); gfid = gf(eye(4),m); if det(randommatrix) ~= 0 invmatrix = inv(randommatrix); check1 = invmatrix * randommatrix; check2 = randommatrix * invmatrix; if (isequal(check1,gfid) & isequal(check2,gfid)) disp('inv found the correct matrix inverse.'); end else disp('The matrix is not invertible.'); end
Вывод от этого примера или этих двух сообщений, в зависимости от того, несингулярна ли случайным образом сгенерированная матрица или сингулярна.
inv found the correct matrix inverse. The matrix is not invertible.
Вычисление Рангов. Чтобы вычислить ранг массива Поля Галуа, используйте функцию rank. Это ведет себя как обычный MATLAB функция rank, когда дали точно один входной параметр. Пример ниже иллюстрирует, как найти ранг квадратных и неквадратных массивов Поля Галуа.
m = 3; asquare = gf([4 7 6; 4 6 5; 0 6 1],m); r1 = rank(asquare); anonsquare = gf([4 7 6 3; 4 6 5 1; 0 6 1 1],m); r2 = rank(anonsquare); [r1 r2]
Вывод
ans =
2 3
Значения r1 и r2 указывают, что asquare имеет меньше, чем полный ранг, но что anonsquare имеет полный ранг.
Факторинг Квадратных Матриц. Чтобы выразить квадратный массив Поля Галуа (или перестановка его) как продукт нижнего треугольного массива Поля Галуа и верхнего треугольного массива Поля Галуа, используйте функцию lu. Эта функция принимает один входной параметр и производит точно два или три выходных аргумента. Это ведет себя как обычный MATLAB функция lu, когда дали тот же синтаксис. Пример ниже иллюстрирует, как учесть использование lu.
tofactor = gf([6 5 7 6; 5 6 2 5; 0 1 7 7; 1 0 5 1],3); [L,U]=lu(tofactor); % lu with two output arguments c1 = isequal(L*U, tofactor) % True tofactor2 = gf([1 2 3 4;1 2 3 0;2 5 2 1; 0 5 0 0],3); [L2,U2,P] = lu(tofactor2); % lu with three output arguments c2 = isequal(L2*U2, P*tofactor2) % True
Решение Линейных уравнений. Чтобы найти конкретное решение линейного уравнения в Поле Галуа, используйте \ или оператор / на массивах Поля Галуа. Приведенная ниже таблица указывает на уравнение, к которому каждый оператор обращается, принимая, что A и B являются ранее заданными массивами Поля Галуа.
| Оператор | Линейное уравнение | Синтаксис | Эквивалентный синтаксис Используя \ |
|---|---|---|---|
Наклонная черта влево (\) | A * x = B | x = A \ B | Не применяется |
Разрежьте (/) | x * A = B | x = B / A | x = (A'\B')' |
Результаты синтаксиса в таблице зависят от характеристик массива Поля Галуа A:
Если A является квадратным и несингулярным, вывод x является уникальным решением линейного уравнения.
Если A является квадратным и сингулярным, синтаксис в таблице производит ошибку.
Если A не является квадратным, MATLAB пытается найти конкретное решение. Если A'*A или A*A' являются сингулярным массивом, или если A является матрицей, где строки превосходят численностью столбцы, который представляет сверхрешительную систему, попытка может перестать работать.
Сообщение об ошибке не обязательно указывает, что линейное уравнение не имеет никакого решения. Вы можете смочь найти решение путем перефразирования проблемы. Например, gf([1 2; 0 0],3) \ gf([1; 0],3) производит ошибку, но математически эквивалентный gf([1 2],3) \ gf([1],3) не делает. Первый синтаксис перестал работать, потому что gf([1 2; 0 0],3) является сингулярной квадратной матрицей.
Пример: решение линейных уравнений
Примеры ниже иллюстрируют, как найти конкретные решения линейных уравнений по Полю Галуа.
m = 4; A = gf(magic(3),m); % Square nonsingular matrix Awide=[A, 2*A(:,3)]; % 3-by-4 matrix with redundancy on the right Atall = Awide'; % 4-by-3 matrix with redundancy at the bottom B = gf([0:2]',m); C = [B; 2*B(3)]; D = [B; B(3)+1]; thesolution = A \ B; % Solution of A * x = B thesolution2 = B' / A; % Solution of x * A = B' ck1 = all(A * thesolution == B) % Check validity of solutions. ck2 = all(thesolution2 * A == B') % Awide * x = B has infinitely many solutions. Find one. onesolution = Awide \ B; ck3 = all(Awide * onesolution == B) % Check validity of solution. % Atall * x = C has a solution. asolution = Atall \ C; ck4 = all(Atall * asolution == C) % Check validity of solution. % Atall * x = D has no solution. notasolution = Atall \ D; ck5 = all(Atall * notasolution == D) % It is not a valid solution.
Вывод от этого примера указывает, что проверки достоверности являются всей истиной (1), за исключением ck5, который является ложным (0).
Разделите Обзор. Можно выполнить некоторые операции обработки сигналов на массивах Поля Галуа, таких как фильтрация, свертка и дискретное преобразование Фурье.
В этом разделе описывается выполнить эти операции.
Другая информация о соответствующих операциях для обычных векторов действительных чисел находится в документации Signal Processing Toolbox™.
Фильтрация. Чтобы отфильтровать вектор Галуа, используйте функцию filter. Это ведет себя как обычный MATLAB функция filter, когда дали точно три входных параметра.
Код и схема ниже дают импульсный ответ конкретного фильтра по GF (2).
m = 1; % Work in GF(2). b = gf([1 0 0 1 0 1 0 1],m); % Numerator a = gf([1 0 1 1],m); % Denominator x = gf([1,zeros(1,19)],m); y = filter(b,a,x); % Filter x. figure; stem(y.x); % Create stem plot. axis([0 20 -.1 1.1])
Свертка. Программное обеспечение Communications Toolbox предлагает два эквивалентных способа применить операцию свертки к паре векторов Галуа:
Используйте функцию conv, как описано в Умножении и Делении Полиномов. Это работает, потому что свертка к двум векторам эквивалентна умножению двух полиномов, коэффициенты которых являются записями векторов.
Используйте функцию convmtx, чтобы вычислить матрицу свертки одного из векторов, и затем умножить ту матрицу на другой вектор. Это работает, потому что свертка к двум векторам эквивалентна фильтрации одного из векторов другим. Эквивалентность разрешает представление цифрового фильтра как матрица свертки, которую можно затем умножить на любой вектор Галуа соответствующей длины.
Если необходимо применить операцию свертки к большим векторам Галуа, умножающимся сверткой, матричная сила быстрее, чем использование conv.
Пример
Вычисляет матрицу свертки для векторного b в GF (4). Представляйте коэффициенты числителя для цифрового фильтра, и затем проиллюстрируйте два эквивалентных способа применить операцию свертки к b с x по Полю Галуа.
m = 2; b = gf([1 2 3]',m); n = 3; x = gf(randi([0 2^m-1],n,1),m); C = convmtx(b,n); % Compute convolution matrix. v1 = conv(b,x); % Use conv to convolve b with x v2 = C*x; % Use C to convolve b with x.
Дискретное преобразование Фурье. Дискретное преобразование Фурье является важным инструментом в цифровой обработке сигналов. Этот тулбокс предлагает эти инструменты, чтобы помочь вам обработать дискретные преобразования Фурье:
fft, который преобразовывает вектор Галуа
ifft, который инвертирует дискретное преобразование Фурье на векторе Галуа
dftmtx, который возвращает массив Поля Галуа, который можно использовать, чтобы выполнить или инвертировать дискретное преобразование Фурье на векторе Галуа
Во всех случаях преобразовываемый вектор должен быть вектором Галуа длины 2m-1 в поле GF (2m). Следующий пример иллюстрирует использование этих функций. Можно проверять, с помощью функции isequal, что y равняется y1, z равняется z1, и z равняется x.
m = 4; x = gf(randi([0 2^m-1],2^m-1,1),m); % A vector to transform alph = gf(2,m); dm = dftmtx(alph); idm = dftmtx(1/alph); y = dm*x; % Transform x using the result of dftmtx. y1 = fft(x); % Transform x using fft. z = idm*y; % Recover x using the result of dftmtx(1/alph). z1 = ifft(y1); % Recover x using ifft.
Если у вас есть много векторов, которые вы хотите преобразовать (в том же поле), это может быть быстрее, чтобы использовать dftmtx однажды и умножение матриц много раз, вместо того, чтобы много раз использовать fft.
Разделите Обзор. Можно использовать векторы Галуа, чтобы представлять полиномы в неопределенном количестве x с коэффициентами в Поле Галуа. Сформируйте представление путем листинга коэффициентов полинома в векторе в порядке убывающих степеней x. Например, вектор
gf([2 1 0 3],4)
представляет полиномиальный Ax3 + 1x2 + 0x + (A+1), где
A является примитивным элементом в поле GF (24).
x является неопределенным количеством в полиноме.
Можно затем использовать такой вектор Галуа, чтобы выполнить арифметику с, оценить и найти корни полиномов. Можно также найти минимальные полиномы элементов Поля Галуа.
Сложение и Вычитание Полиномов. Чтобы добавить и вычесть полиномы, используйте + и - на равной длине векторы Галуа, которые представляют полиномы. Если один полином имеет более низкую степень, чем другой, необходимо заполнить более короткий вектор нулями вначале, таким образом, эти два вектора имеют ту же длину. Пример ниже показов, как добавить степень один и степень два полинома.
lin = gf([4 2],3); % A^2 x + A, which is linear in x linpadded = gf([0 4 2],3); % The same polynomial, zero-padded quadr = gf([1 4 2],3); % x^2 + A^2 x + A, which is quadratic in x % Can't do lin + quadr because they have different vector lengths. sumpoly = [0, lin] + quadr; % Sum of the two polynomials sumpoly2 = linpadded + quadr; % The same sum
Умножение и Деление Полиномов. Чтобы умножить и разделить полиномы, используйте conv и deconv на векторах Галуа, которые представляют полиномы. Умножение и деление полиномов эквивалентны свертке и развертке векторов. Функция deconv возвращает частное этих двух полиномов, а также полинома остатка. Примеры ниже.
m = 4; apoly = gf([4 5 3],m); % A^2 x^2 + (A^2 + 1) x + (A + 1) bpoly = gf([1 1],m); % x + 1 xpoly = gf([1 0],m); % x % Product is A^2 x^3 + x^2 + (A^2 + A) x + (A + 1). cpoly = conv(apoly,bpoly); [a2,remd] = deconv(cpoly,bpoly); % a2==apoly. remd is zero. [otherpol,remd2] = deconv(cpoly,xpoly); % remd is nonzero.
Операторы умножения и операторы деления в Арифметике в Полях Галуа умножают элементы или матрицы, не полиномы.
Оценка многочленов. Чтобы оценить полином в элементе Поля Галуа, используйте polyval. Это ведет себя как обычный MATLAB функция polyval, когда дали точно два входных параметра. Пример ниже оценивает полином в нескольких элементах в поле и проверяет результаты с помощью .^ и .* в поле.
m = 4; apoly = gf([4 5 3],m); % A^2 x^2 + (A^2 + 1) x + (A + 1) x0 = gf([0 1 2],m); % Points at which to evaluate the polynomial y = polyval(apoly,x0) a = gf(2,m); % Primitive element of the field, corresponding to A. y2 = a.^2.*x0.^2 + (a.^2+1).*x0 + (a+1) % Check the result.
Вывод ниже.
y = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
3 2 10
y2 = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
3 2 10
Первый элемент y оценивает полином в 0 и, поэтому, возвращает постоянный термин полинома 3.
Корни многочленов. Чтобы найти корни полинома в Поле Галуа, используйте функцию roots на векторе Галуа, который представляет полином. Эта функция находит корни, которые находятся в том же поле, в котором находится вектор Галуа. Число раз запись появляется в выходном векторе от roots, является точно своей кратностью как корнем полинома.
Если вектор Галуа находится в GF (2 м), полином, который это представляет, может иметь дополнительные корни в некотором дополнительном поле GF ((2 м) k). Однако roots не находит те дополнительные корни или указывает на их существование.
Примеры ниже корней находки кубических полиномов в GF (8).
p = 3; m = 2; field = gftuple([-1:p^m-2]',m,p); % List of all elements of GF(9) % Use default primitive polynomial here. polynomial = [1 0 1 1]; % 1 + x^2 + x^3 rts =gfroots(polynomial,m,p) % Find roots in exponential format % Check that each one is actually a root. for ii = 1:3 root = rts(ii); rootsquared = gfmul(root,root,field); rootcubed = gfmul(root,rootsquared,field); answer(ii)= gfadd(gfadd(0,rootsquared,field),rootcubed,field); % Recall that 1 is really alpha to the zero power. % If answer = -Inf, then the variable root represents % a root of the polynomial. end answer
Корни Бинарных Полиномов. В особом случае полинома, имеющего бинарные коэффициенты, также легко найти корни, которые существуют в дополнительном поле. Это вызвано тем, что элементы 0 и 1 имеют то же однозначное представительство во всех полях характеристических двух. Чтобы найти корни бинарного полинома в дополнительном поле, примените функцию roots к вектору Галуа в дополнительном поле, элементы массива которого являются бинарными коэффициентами полинома.
Пример ниже ищет корни бинарного полинома в различных полях.
gf2poly = gf([1 1 1],1); % x^2 + x + 1 in GF(2) noroots = roots(gf2poly); % No roots in the ground field, GF(2) gf4poly = gf([1 1 1],2); % x^2 + x + 1 in GF(4) roots4 = roots(gf4poly); % The roots are A and A+1, in GF(4). gf16poly = gf([1 1 1],4); % x^2 + x + 1 in GF(16) roots16 = roots(gf16poly); % Roots in GF(16) checkanswer4 = polyval(gf4poly,roots4); % Zero vector checkanswer16 = polyval(gf16poly,roots16); % Zero vector
Корни полинома не существуют в GF (2), таким образом, noroots является пустым массивом. Однако корни полинома существуют в GF (4), а также в GF (16), таким образом, roots4 и roots16 непусты.
Заметьте, что roots4 и roots16 не равны друг другу. Они отличаются этими способами:
roots4 является GF (4) массив, в то время как roots16 является GF (16) массив. MATLAB отслеживает базовое поле массива Поля Галуа.
Элементы массива в roots4 и roots16 отличаются, потому что они используют представления относительно различных примитивных полиномов. Например, 2 (который представляет примитивный элемент) является элементом векторного roots4, потому что примитивный полином по умолчанию для GF (4) является тем же полиномом, который представляет gf4poly. С другой стороны, 2 не является элементом roots16, потому что примитивный элемент GF (16) не является корнем полинома, который представляет gf16poly.
Минимальные Полиномы. Минимальный полином элемента GF (2 м) является наименьшей степенью ненулевой полином бинарного коэффициента, имеющий тот элемент как корень в GF (2 м). Чтобы найти минимальный полином элемента или вектор-столбец элементов, используйте функцию minpol.
Код ниже находок, что минимальный полином gf(6,4) является D2 + D + 1 и затем проверяет, что gf(6,4) действительно среди корней того полинома в поле GF (16).
m = 4; e = gf(6,4); em = minpol(e) % Find minimal polynomial of e. em is in GF(2). emr = roots(gf([0 0 1 1 1],m)) % Roots of D^2+D+1 in GF(2^m)
Вывод
em = GF(2) array.
Array elements =
0 0 1 1 1
emr = GF(2^4) array. Primitive polynomial = D^4+D+1 (19 decimal)
Array elements =
6
7
Чтобы узнать, какие элементы Поля Галуа совместно используют тот же минимальный полином, используйте функцию cosets.
Разделите Обзор. В этом разделе описываются методы для управления переменными Галуа или для передачи информации между массивами Поля Галуа и обычными массивами MATLAB.
Эти методы особенно релевантны, если вы пишете функциям файла MATLAB то Поле Галуа процесса массивы. Для примера этого типа использования введите edit gf/conv в Командном окне и исследуйте первые несколько строк кода в окне редактора.
Определение, Является ли Переменная Массивом Поля Галуа. Чтобы узнать, является ли переменная массивом Поля Галуа, а не обычным массивом MATLAB, используйте функцию isa. Рисунок ниже.
mlvar = eye(3); gfvar = gf(mlvar,3); no = isa(mlvar,'gf'); % False because mlvar is not a Galois array yes = isa(gfvar,'gf'); % True because gfvar is a Galois array
Извлечение информации от Массива Поля Галуа. Чтобы извлечь элементы массива, полевой порядок или примитивный полином от переменной, которая является массивом Поля Галуа, добавляет суффикс к имени переменной. Таблица ниже приводит точные суффиксы, которые независимы от имени переменной.
| Информация | Суффикс | Выходное значение |
|---|---|---|
| Элементы массива | .x | Массив MATLAB типа uint16, который содержит значения данных от массива Поля Галуа. |
| Полевой порядок | .m | Целое число типа double, который указывает, что массив Поля Галуа находится в GF (2^m). |
| Примитивный полином | .prim_poly | Целое число типа uint32, который представляет примитивный полином. Представление подобно описанию в том, Как Целые числа Соответствуют Элементам Поля Галуа. |
Если выходное значение является целочисленным типом данных, и вы хотите преобразовать его в double для более поздней манипуляции, использовать функцию double.
Код ниже иллюстрирует использование этих суффиксов. Определение empr использует вектор бинарных коэффициентов полинома, чтобы создать массив Поля Галуа в дополнительном поле. Другая часть примера получает примитивный полином для поля и преобразовывает его в бинарное векторное представление, имеющее соответствующее количество битов.
% Check that e solves its own minimal polynomial. e = gf(6,4); % An element of GF(16) emp = minpol(e); % The minimal polynomial, emp, is in GF(2). empr = roots(gf(emp.x,e.m)); % Find roots of emp in GF(16). % Check that the primitive element gf(2,m) is % really a root of the primitive polynomial for the field. primpoly_int = double(e.prim_poly); mval = e.m; primpoly_vect = gf(de2bi(primpoly_int,mval+1,'left-msb'),mval); containstwo = roots(primpoly_vect); % Output vector includes 2.
Преобразование массива поля Галуа к удваивается
a = gf([1,0]) b = double(a.x) %a.x is in uint16
MATLAB возвращает следующее:
a = GF(2) array.
Array elements =
1 0
b =
1 0Определение Примитивного Полинома описывает, как представлять элементы Поля Галуа относительно примитивного полинома по вашему выбору. В этом разделе описывается можно увеличить скорость вычислений, включающих массив Поля Галуа, который использует примитивный полином кроме примитивного полинома по умолчанию. Метод рекомендуется, если вы выполняете много таких вычислений.
Механизм для увеличения скорости является файлом данных, userGftable.mat, что некоторое вычислительное использование функций, чтобы не выполнять определенные вычисления неоднократно. Использовать в своих интересах этот механизм для вашей комбинации полевого порядка (m) и примитивный полином (prim_poly):
Перейдите в приложении MATLAB к папке, к которой у вас есть разрешение записи. Можно использовать или функцию cd или функцию Текущей папки, чтобы перейти.
Задайте m и prim_poly как переменные рабочей области. Например:
m = 3; prim_poly = 13; % Examples of valid values
Вызовите функцию gftable:
gftable(m,prim_poly); % If you previously defined m and prim_poly
Функция пересматривает или создает userGftable.mat в вашей текущей рабочей папке, чтобы включать данные, относящиеся к вашей комбинации полевого порядка и примитивного полинома. После того, как вы первоначально инвестируете время, чтобы вызвать gftable, последующие вычисления с помощью тех значений m и prim_poly должны быть быстрее.
Если вы изменяете свою текущую рабочую директорию после вызова gftable, необходимо поместить userGftable.mat в путь MATLAB, чтобы гарантировать, что MATLAB видит его. Сделайте это при помощи команды addpath, чтобы снабдить префиксом директорию, содержащую userGftable.mat к вашему пути MATLAB. Если у вас есть несколько копий userGftable.mat на вашем пути, используйте which('userGftable.mat','-all'), чтобы узнать, где они и который использует один MATLAB.
Чтобы видеть, как много gftable улучшает скорость ваших вычислений, можно окружить вычисления функциями toc и tic. Смотрите страницу с описанием gftable для примера.
[1] Blahut, Ричард Э., Теория и Практика Кодов Контроля ошибок, Чтения, MA, Аддисона-Уэсли, 1983, p. 105.
[2] Ленг, саржа, алгебра, третий выпуск, чтение, MA, Аддисон-Уэсли, 1993.
[3] Лин, Шу, и Дэниел Дж. Костелло младший, кодирование контроля ошибок: основные принципы и приложения, Englewood Cliffs, NJ, Prentice Hall, 1983.
[4] Линт фургона, J. H. Введение в Кодинг-Зэори, Нью-Йорк, Springer-Verlag, 1982.
[5] Ивовый прут, Стивен Б., системы контроля ошибок для цифровой связи и устройства хранения данных, верхнего Сэддл-Ривер, NJ, Prentice Hall, 1995.
Поле Галуа является алгебраическим полем, имеющим элементы pm, где p является главным, и m является положительным целым числом. В этой главе описываются, как работать с Полями Галуа, в которых p нечетен. Чтобы работать с Полями Галуа, имеющими четное число элементов, смотрите Вычисления Поля Галуа. Разделы в этой главе следующие.
В этом разделе p является нечетным простым числом, и m является положительным целым числом.
Кроме того, этот документ использует несколько терминов, которые последовательно не используются в литературе. Определения, принятые здесь, появляются в Линте фургона [5].
Примитивный элемент GF (pm), циклический генератор группы ненулевых элементов GF (pm). Это означает, что каждый ненулевой элемент поля может быть выражен как примитивный элемент, возведенный к некоторой целочисленной степени. Примитивные элементы называются в этом разделе.
Примитивный полином для GF (pm), минимальный полином некоторого примитивного элемента GF (pm). Как следствие это имеет степень m и неприводимо.
Разделите Обзор. В этом разделе рассматриваются, как представлять элементы Поля Галуа с помощью экспоненциального формата этого тулбокса и полиномиального формата. Это также описывает способ перечислить все элементы Поля Галуа, потому что некоторые функции используют такой список в качестве входного параметра. Наконец, это обсуждает групповые из представлений элементов Поля Галуа.
Элементы GF (p) могут быть представлены с помощью целых чисел от 0 до p-1.
Когда m - по крайней мере 2, GF (pm) называется дополнительным полем. Одни только Целые числа не могут представлять элементы GF (pm) прямым способом. MATLAB техническое вычислительное программное обеспечение использует два основных соглашения для представления элементов GF (pm): экспоненциальный формат и полиномиальный формат.
И экспоненциальный формат и полиномиальный формат относительно вашего выбора конкретного примитивного элемента GF (pm).
Экспоненциальный формат. Этот формат использует свойство, что каждый ненулевой элемент GF (pm), может быть выражен как Ac для некоторого целого числа c между 0 и pm-2. Более высокие экспоненты не нужны, потому что теория Полей Галуа подразумевает, что каждый ненулевой элемент GF (pm), удовлетворяет уравнению xq-1 = 1 где q = пополудни.
Использование экспоненциального формата показывают в приведенной ниже таблице.
| Элемент GF (pm) | Представление MATLAB элемента |
|---|---|
| 0 | -Inf |
| A0 = 1 | 0 |
| A1 | 1 |
| ... | ... |
Aq-2, где q = пополудни
| q-2
|
Несмотря на то, что -Inf является стандартным экспоненциальным представлением нулевого элемента, все отрицательные целые числа эквивалентны -Inf, когда используется в качестве входных параметров в экспоненциальном формате. Эта эквивалентность может быть полезной; например, смотрите краткую строку кода в конце раздела Default Primitive Polynomials.
Эквивалентность всех отрицательных целых чисел и -Inf как экспоненциальные форматы означает, что, например,-1 не представляет A-1, мультипликативную инверсию A. Вместо этого-1 представляет нулевой элемент поля.
Полиномиальный Формат. Полиномиальный формат использует свойство, что каждый элемент GF (pm), может быть выражен как полином в с экспонентами между 0 и m-1 и коэффициенты в GF (p). В полиномиальном формате, элементе
A(1) + A(2) + A(3) A2 + ... + Am A(m) 1
представлен в MATLAB вектором
[A(1) A(2) A(3) ... A(m)]
Функции Поля Галуа в этом тулбоксе представляют полином как вектор, который перечисляет коэффициенты в порядке возрастающих степеней переменной. Это - противоположность порядка, который используют другие функции MATLAB.
Список Всех Элементов Поля Галуа. Некоторые функции Поля Галуа в этом тулбоксе требуют аргумента, который перечисляет все элементы дополнительного поля GF (pm). Это снова относительно конкретного примитивного элемента GF (pm). Соответствующий формат для списка элементов является соответствующим форматом матрицы, имеющей строки pm, один для каждого элемента поля. Матрица имеет m столбцы, один для каждого коэффициента степени в полиномиальном формате, показанном в Полиномиальном Формате выше. Первая строка содержит только нули, потому что она соответствует нулевому элементу в GF (pm). Если k между 2 и пополудни, то kth строка задает полиномиальный формат элемента Ak-2.
Минимальный полином средства в вычислении этой матрицы, потому что это говорит, как выразить Am с точки зрения более низких степеней A. Например, таблица ниже приводит элементы GF (32), где A является корнем примитивного полинома 2 + 2x + x2. Этот полином позволяет повторенное использование замены
A2 = -2 - 2 А = 1 + A
при выполнении вычислений в среднем столбце таблицы.
Элементы GF (9)
| Экспоненциальный формат | Полиномиальный формат | Строка матрицы MATLAB элементов |
|---|---|---|
| A-Inf | 0 | 0 0 |
| A0 | 1 | 1 0 |
| A1 | A | 0 1 |
| A2 | 1+A | 1 1 |
| A3 | + A2 = + 1 + = 1 + 2 А | 1 2 |
| A4 | + 2A2 = + 2 + 2 А = 2 | 2 0 |
| A5 | 2 А | 0 2 |
| A6 | 2A2 = 2 + 2 А | 2 2 |
| A7 | 2 А + 2A2 = 2 А + 2 + 2 А = 2 + A | 2 1 |
Пример
Автоматический способ сгенерировать матрицу, строки которой находятся в третьем столбце приведенной выше таблицы, состоит в том, чтобы использовать код ниже.
p = 3; m = 2;
% Use the primitive polynomial 2 + 2x + x^2 for GF(9).
prim_poly = [2 2 1];
field = gftuple([-1:p^m-2]',prim_poly,p);Функция gftuple обсуждена более подробно в Преобразовании и Упрощении Форматов элемента.
Групповой из Представлений. Данное поле имеет больше чем один примитивный элемент. Если два примитивных элемента будут иметь различные минимальные полиномы, то соответствующие матрицы элементов будут иметь свои строки в различном порядке. Если два примитивных элемента совместно используют тот же минимальный полином, то матрица элементов поля является тем же самым.
Можно использовать любой примитивный элемент, который вы хотите, пока вы понимаете, как вводы и выводы функций Поля Галуа зависят от выбора некоторого примитивного полинома. Обычно лучше использовать тот же примитивный полином в данном скрипте или функции.
Другие пути, которыми представления элементов не уникальны, возникают из уравнений, которые удовлетворяют элементы Поля Галуа. Например, экспоненциальный формат 8 в GF (9) является действительно тем же самым как экспоненциальным форматом 0, потому что A8 = 1 = A0 в GF (9). Как другой пример, замена, упомянутая непосредственно перед тем, как, таблица Elements GF (9) показывает, что полиномиальный формат [0 0 1] является действительно тем же самым как полиномиальным форматом [1 1].
Этот тулбокс обеспечивает примитивный полином по умолчанию для каждого дополнительного поля. Можно получить этот полином с помощью функции gfprimdf. Команда
prim_poly = gfprimdf(m,p); % If m and p are already defined
производит стандартное представление вектора - строки минимального полинома по умолчанию для GF (pm).
Например, команда ниже показов, что примитивный полином по умолчанию для GF (9) равняется 2 + x + x2, не полином, используемый в Списке Всех Элементов Поля Галуа.
poly1=gfprimdf(2,3);
poly1 =
2 1 1
Чтобы сгенерировать список элементов GF (pm) использование примитивного полинома по умолчанию, используйте команду
field = gftuple([-1:p^m-2]',m,p);
Преобразование в Самый Простой Полиномиальный Формат. Функция gftuple производит самое простое полиномиальное представление элемента GF (pm), или, учитывая экспоненциальное представление или, учитывая полиномиальное представление того элемента. Это может быть полезно для генерации списка элементов GF (pm), которого требуют другие функции.
Используя gftuple требует трех аргументов: одно представление элемента GF (pm), одно указание на примитивный полином, который MATLAB техническое вычислительное программное обеспечение должен использовать при вычислении вывода и главного p. Приведенная ниже таблица указывает, как gftuple ведет себя, когда дали первые два аргумента в различных форматах.
Поведение gftuple В зависимости от Формата Первых Двух Входных параметров
| Как указать элемент | Как указать на примитивный полином | Что Производит gftuple |
|---|---|---|
| Экспоненциальный формат; c = любое целое число | Целочисленный m> 1 | Полиномиальный формат Ac, где A является корнем примитивного полинома по умолчанию для GF (pm), |
Example: tp = gftuple(6,2,3); % c = 6 here
| ||
| Экспоненциальный формат; c = любое целое число | Вектор коэффициентов примитивного полинома | Полиномиальный формат Ac, где A является корнем данного примитивного полинома |
Пример: polynomial = gfprimdf(2,3); tp = gftuple(6,polynomial,3); % c = 6 here
| ||
| Полиномиальный формат любой степени | Целочисленный m> 1 | Полиномиальный формат степени <m, с помощью примитивного полинома по умолчанию для GF (pm), чтобы упростить |
Пример: tp = gftuple([0 0 0 0 0 0 1],2,3);
| ||
| Полиномиальный формат любой степени | Вектор коэффициентов примитивного полинома | Полиномиальный формат степени <m, с помощью данного примитивного полинома для GF (pm), чтобы упростить |
Пример: polynomial = gfprimdf(2,3); tp = gftuple([0 0 0 0 0 0 1],polynomial,3);
| ||
Четыре примера, которые появляются в таблице, прежде всего, производят тот же векторный tp = [2, 1], но их различные входные параметры к gftuple соответствуют строкам таблицы. Каждый пример выражает то, что A6 = 2+A, где A является корнем примитивного полинома (по умолчанию) 2 + x + x2 для GF (32).
Пример
Этот пример показывает, как gfconv и gftuple объединяются, чтобы умножить два полиномиальных элемента формата GF (34). Первоначально, gfconv умножает эти два полинома, обрабатывая примитивный элемент, как будто это была переменная. Это производит старший полином, который gftuple упрощает использование полиномиального уравнения, которому удовлетворяет примитивный элемент. Конечным результатом является самый простой полиномиальный формат продукта.
p = 3; m = 4; a = [1 2 0 1]; b = [2 2 1 2]; notsimple = gfconv(a,b,p) % a times b, using high powers of alpha simple = gftuple(notsimple,m,p) %Highest exponent of alpha is m-1
Вывод ниже.
notsimple =
2 0 2 0 0 1 2
simple =
2 1 0 1
Пример: Генерация Списка Элементов Поля Галуа. Этот пример применяет функциональность преобразования к задаче генерации матрицы, которая перечисляет все элементы Поля Галуа. Матрица, которая перечисляет все полевые элементы, является входным параметром в функциях, таких как gfadd и gfmul. Переменные field1 и field2 ниже имеют формат, который ожидают такие функции.
p = 5; % Or any prime number m = 4; % Or any positive integer field1 = gftuple([-1:p^m-2]',m,p); prim_poly = gfprimdf(m,p); % Or any primitive polynomial % for GF(p^m) field2 = gftuple([-1:p^m-2]',prim_poly,p);
Преобразование в Самый Простой Экспоненциальный формат. Тот же функциональный gftuple также производит самое простое экспоненциальное представление элемента GF (pm), или, учитывая экспоненциальное представление или, учитывая полиномиальное представление того элемента. Чтобы получить этот вывод, используйте синтаксис
[polyformat, expformat] = gftuple(...)
Формат ввода и вывод polyformat как в таблице Behavior gftuple В зависимости от Формата Первых Двух Входных параметров. Кроме того, переменная expformat содержит самый простой экспоненциальный формат элемента, представленного в polyformat. Это является самым простым в том смысле, что экспонентой является или -Inf или номер между 0 и pm-2.
Пример
Чтобы восстановить экспоненциальный формат элемента 2 + что рассмотренный предыдущий раздел, используйте команды ниже. В этом случае polyformat содержит избыточную информацию, в то время как expformat содержит желаемый результат.
[polyformat, expformat] = gftuple([2 1],2,3)
polyformat =
2 1
expformat =
6
Этот вывод, кажется, сначала противоречит информации в таблице Elements GF (9) , но на самом деле это не делает. Таблица использует различный примитивный элемент; два плюс тот примитивный элемент имеет полиномиальные и экспоненциальные форматы, показанные ниже.
prim_poly = [2 2 1]; [polyformat2, expformat2] = gftuple([2 1],prim_poly,3)
Вывод ниже отражений информация в нижней строке таблицы.
polyformat2 =
2 1
expformat2 =
7
Разделите Обзор. Можно добавить, вычесть, умножить и разделить элементы Полей Галуа с помощью функций gfadd, gfsub, gfmul и gfdiv, соответственно. Каждая из этих функций имеет режим для лучших полей и режим для дополнительных полей.
Арифметика в Лучших Полях. Арифметика в GF (p) совпадает с арифметическим p по модулю. gfadd функций, gfmul, gfsub и gfdiv принимают два аргумента, которые представляют элементы GF (p) как целые числа между 0 и p-1. Третий аргумент задает p.
Пример: таблица сложения для GF (5)
Код ниже создает таблицу сложения для GF (5). Если a и b между 0 и 4, то элемент gfp_add(a+1,b+1) представляет сумму a+b в GF (5). Например, gfp_add(3,5) = 1, потому что 2+4 1 5 по модулю.
p = 5; row = 0:p-1; table = ones(p,1)*row; gfp_add = gfadd(table,table',p)
Вывод для этого примера следует.
gfp_add =
0 1 2 3 4
1 2 3 4 0
2 3 4 0 1
3 4 0 1 2
4 0 1 2 3
Другие значения p производят таблицы для различных лучших полей GF (p). Заменение gfadd gfmul, gfsub или gfdiv производит таблицу для соответствующей арифметической операции в GF (p).
Арифметика в Дополнительных Полях. Те же арифметические функции могут добавить элементы GF (pm), когда m> 1, но формат аргументов более сложен, чем в случае выше. В целом арифметика в дополнительных полях более сложна, чем арифметика в лучших полях; смотрите работы, перечисленные в Выбранной Библиографии для Полей Галуа для получения дополнительной информации о том, как арифметические операции работают.
При работе в дополнительных полях функции gfadd, gfmul, gfsub и gfdiv используют первые два аргумента, чтобы представлять элементы GF (pm) в экспоненциальном формате. Третий аргумент, который требуется, перечисляет все элементы GF (pm), как описано в Списке Всех Элементов Поля Галуа. Результат находится в экспоненциальном формате.
Пример: таблица сложения для GF (9)
Код ниже создает таблицу сложения для GF (32), с помощью экспоненциальных форматов относительно корня примитивного полинома по умолчанию для GF (9). Если a и b между-1 и 7, то элемент gfpm_add(a+2,b+2) представляет сумму Aa и Ab в GF (9). Например, gfpm_add(4,6) = 5, потому что
A2 + A4 = A5
Используя четвертые и шестые строки матричного field, можно проверить это
A2 + A4 = (1 + 2 А) + (2 + 0A) = 3 + 2 А = 0 + 2 А = A5 по модулю 3.
p = 3; m = 2; % Work in GF(3^2). field = gftuple([-1:p^m-2]',m,p); % Construct list of elements. row = -1:p^m-2; table = ones(p^m,1)*row; gfpm_add = gfadd(table,table',field)
Вывод ниже.
gfpm_add =
-Inf 0 1 2 3 4 5 6 7
0 4 7 3 5 -Inf 2 1 6
1 7 5 0 4 6 -Inf 3 2
2 3 0 6 1 5 7 -Inf 4
3 5 4 1 7 2 6 0 -Inf
4 -Inf 6 5 2 0 3 7 1
5 2 -Inf 7 6 3 1 4 0
6 1 3 -Inf 0 7 4 2 5
7 6 2 4 -Inf 1 0 5 3
Если бы вы использовали различный примитивный полином, то таблицы выглядели бы по-другому. Это целесообразно, потому что упорядоченное расположение строк и столбцов таблиц было основано на том конкретном выборе примитивного полинома а не на любом естественном упорядоченном расположении элементов GF (9).
Другие значения p и m производят таблицы для различных дополнительных полей GF (p^m). Заменение gfadd gfmul, gfsub или gfdiv производит таблицу для соответствующей арифметической операции в GF (p^m).
Разделите Обзор. Полином по GF (p) является полиномом, коэффициенты которого являются элементами GF (p). Программное обеспечение Communications Toolbox обеспечивает функции для
Изменение полиномов косметическими способами
Выполнение полиномиальной арифметики
Охарактеризование полиномов как примитивные или неприводимые
Нахождение корней полиномов в Поле Галуа
Функции Поля Галуа в этом тулбоксе представляют полином по GF (p) для нечетных значений p как вектор, который перечисляет коэффициенты в порядке возрастающих степеней переменной. Это - противоположность порядка, который используют другие функции MATLAB.
Косметические Изменения Полиномов. Чтобы отобразить традиционно отформатированный полином, который соответствует вектору - строке, содержащему коэффициенты, используйте gfpretty. Чтобы обрезать полином путем удаления всех условий нулевого коэффициента, которые имеют экспоненты выше, чем степень полинома, используйте gftrunc. Например,
polynom = gftrunc([1 20 394 10 0 0 29 3 0 0]) gfpretty(polynom)
Вывод ниже.
polynom =
1 20 394 10 0 0 29 3
2 3 6 7
1 + 20 X + 394 X + 10 X + 29 X + 3 X
Если вы не используете шрифт фиксированной ширины, то интервал в отображении не может выглядеть правильным.
Полиномиальная Арифметика. Функции gfadd и gfsub добавляют и вычитают, соответственно, полиномы по GF (p). Функция gfconv умножает полиномы по GF (p). Функция gfdeconv делит полиномы на GF (p), производя полином частного и полином остатка. Например, команды ниже показа, что 2 + x + x2 времена 1 + x по полю GF (3) 2 + 2x2 + x3.
a = gfconv([2 1 1],[1 1],3) [quot, remd] = gfdeconv(a,[2 1 1],3)
Вывод ниже.
a =
2 0 2 1
quot =
1 1
remd =
0
Ранее обсужденные функции gfadd и gfsub добавляют и вычитают, соответственно, полиномы. Поскольку это использует вектор коэффициентов, чтобы представлять полином, MATLAB не различает добавление двух полиномов и добавление двух векторов - строк поэлементно.
Характеристика Полиномов. Учитывая полином по GF (p), функция gfprimck определяет, неприводимо ли это и/или примитивно. По определению, если это примитивно затем, это неприводимо; однако, реверс не обязательно верен. gfprimdf и функции gfprimfd возвращают примитивные полиномы.
Учитывая элемент GF (pm), функция gfminpol вычисляет свой минимальный полином по GF (p).
Пример
Например, код ниже отражений неприводимость всех минимальных полиномов. Однако минимальный полином непримитивного элемента не является примитивным полиномом.
p = 3; m = 4; % Use default primitive polynomial here. prim_poly = gfminpol(1,m,p); ckprim = gfprimck(prim_poly,p); % ckprim = 1, since prim_poly represents a primitive polynomial. notprimpoly = gfminpol(5,m,p); cknotprim = gfprimck(notprimpoly,p); % cknotprim = 0 (irreducible but not primitive) % since alpha^5 is not a primitive element when p = 3. ckreducible = gfprimck([0 1 1],p); % ckreducible = -1 since the polynomial is reducible.
Корни многочленов. Учитывая полином по GF (p), функция gfroots находит корни полинома в подходящем дополнительном поле GF (pm). Существует два способа сказать MATLAB степень m дополнительного поля GF (pm), как показано в следующей таблице.
Форматы для Второго Аргумента gfroots
| Второй аргумент | Представляет |
|---|---|
| Положительное целое число | m как в GF (pm). MATLAB использует примитивный полином по умолчанию в своих вычислениях. |
| Вектор - строка | Примитивный полином для GF (pm). Здесь m является степенью этого примитивного полинома. |
Пример: корни полинома в GF (9)
Код ниже корней находок полинома 1 + x2 + x3 в GF (9) и затем проверяет, что они - действительно корни. Экспоненциальный формат элементов GF (9) используется повсюду.
p = 3; m = 2; field = gftuple([-1:p^m-2]',m,p); % List of all elements of GF(9) % Use default primitive polynomial here. polynomial = [1 0 1 1]; % 1 + x^2 + x^3 rts =gfroots(polynomial,m,p) % Find roots in exponential format % Check that each one is actually a root. for ii = 1:3 root = rts(ii); rootsquared = gfmul(root,root,field); rootcubed = gfmul(root,rootsquared,field); answer(ii)= gfadd(gfadd(0,rootsquared,field),rootcubed,field); % Recall that 1 is really alpha to the zero power. % If answer = -Inf, then the variable root represents % a root of the polynomial. end answer
Вывод показывает, что A0 (который равняется 1), A5 и A7 являются корнями.
roots =
0
5
7
answer =
-Inf -Inf -Inf
Смотрите страницу с описанием для gfroots, чтобы видеть, как gfroots может также предоставить вам полиномиальные форматы корней и список всех элементов поля.
Смотрите онлайновые страницы с описанием для получения информации об этих других функциях Поля Галуа в программном обеспечении Communications Toolbox:
[1] Blahut, Ричард Э., теория и практика кодов контроля ошибок, чтения, массы., Аддисон-Уэсли, 1983.
[2] Ленг, саржа, алгебра, третий выпуск, чтение, масса., Аддисон-Уэсли, 1993.
[3] Лин, Шу, и Дэниел Дж. Костелло младший, кодирование контроля ошибок: основные принципы и приложения, Englewood Cliffs, Нью-Джерси, Prentice Hall, 1983.
[4] Линт фургона, J. H. Введение в Кодинг-Зэори, Нью-Йорк, Springer-Verlag, 1982.