getDelayModel

Представление пространства состояний внутренних задержек

Синтаксис

[H,tau] = getDelayModel(sys) [A,B1,B2,C1,C2,D11,D12,D21,D22,E,tau] = getDelayModel(sys)

Описание

[H,tau] = getDelayModel(sys) анализирует модель в пространстве состояний sys с внутренними задержками в модель в пространстве состояний без задержек, H и вектор внутренних задержек, tau. Отношение среди sys, H и tau показывают в следующей схеме.

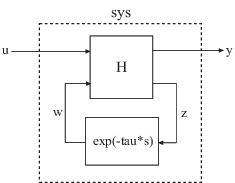
[A,B1,B2,C1,C2,D11,D12,D21,D22,E,tau] = getDelayModel(sys) возвращает набор матриц пространства состояний и внутреннего вектора задержки, tau, которые явным образом описывают модель в пространстве состояний sys. Эти матрицы пространства состояний заданы уравнениями пространства состояний:

Непрерывно-разовый sys:
$\begin{matrix} E \frac{d x (t)}{d t} = A x (t) + B_{1} u (t) + B_{2} w (t) \\ y (t) = C_{1} x (t) + D_{11} u (t) + D_{12} w (t) \\ z (t) = C_{2} x (t) + D_{21} u (t) + D_{22} w (t) \\ w (t) = z (t - τ) \end{matrix}$
Дискретное время sys:
$\begin{matrix} E x [k + 1] = A x [k] + B_{1} u [k] + B_{2} w [k] \\ y [k] = C_{1} x [k] + D_{11} u [k] + D_{12} w [k] \\ z [k] = C_{2} x [k] + D_{21} u [k] + D_{22} w [k] \\ w [k] = z [k - τ] \end{matrix}$

Входные параметры

sys

Любая модель (ss) пространства состояний.

Выходные аргументы

H

Модель в пространстве состояний без задержек (ss). результаты H разложения sys на компонент без задержек и exp(-tau*s) компонента, который представляет все внутренние задержки.

Если sys не имеет никаких внутренних задержек, H равен sys.

tau

Вектор внутренних задержек sys, выраженного в единицах измерения времени sys. Векторные результаты tau разложения sys в модель в пространстве состояний без задержек H и exp(-tau*s) компонента, который представляет все внутренние задержки.

Если sys не имеет никаких внутренних задержек, tau пуст.

A,B1,B2,C1,C2,D11,D12,D21,D22,E

Набор матриц пространства состояний, что, с внутренним вектором задержки tau, явным образом описывают модель в пространстве состояний sys.

Для явных моделей в пространстве состояний (E = I или sys.e = []), вывод E = [].

Если sys не имеет никаких внутренних задержек, выходных параметров B2, C2, D12, D21, и D22 весь пуст ([]).

Примеры

свернуть все

Получите модель в пространстве состояний без Задержек и внутреннюю задержку

Скрипт Open Live Script

Анализируйте следующую систему с обратной связью с внутренней задержкой на компонент без задержек и компонент, представляющий внутреннюю задержку.

Создайте модель sys с обратной связью от r до y.

G = tf(1,[1 10],'InputDelay',2.1); 
C = pid(0.5,2.3);
sys = feedback(C*G,1);

sys является моделью (ss) пространства состояний с внутренней задержкой, которая является результатом закрытия обратной связи на объекте с входной задержкой.

Разложите sys на модель в пространстве состояний без задержек и значение внутренней задержки.

[H,tau] = getDelayModel(sys);

Подтвердите, что внутренняя задержка совпадает с исходной входной задержкой на объекте.

tau

tau = 2.1000

Смотрите также

setDelayModel

Темы

Внутренние задержки

Документация