Линейно-квадратично-интегральное управление
[K,S,e] = lqi(SYS,Q,R,N)
lqi вычисляет оптимальный закон управления с обратной связью состояния для цикла отслеживания, показанного в следующей фигуре.
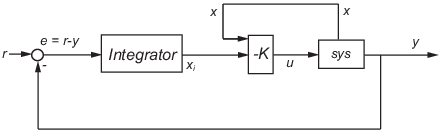
Для объекта sys с уравнениями пространства состояний (или их дискретный дубликат):
управление с обратной связью состояния имеет форму
где xi является интегратором вывод. Этот закон о надзоре гарантирует, что вывод y отслеживает ссылочную команду r. Для систем MIMO количество интеграторов равняется размерности вывода y.
[K,S,e] = lqi(SYS,Q,R,N) вычисляет оптимальную матрицу усиления K, учитывая модель в пространстве состояний SYS для объекта и матриц взвешивания Q, R, N. Закон о надзоре u = –Kz = –K [x; xi] минимизирует следующие функции стоимости (для r = 0)
в течение непрерывного времени
в течение дискретного времени
В дискретное время lqi вычисляет интегратор вывод xi с помощью прямой Эйлеровой формулы
где Ts является шагом расчета SYS.
Когда вы не используете матричный N, N установлен в 0. lqi также возвращает решение S связанного алгебраического уравнения Riccati и собственных значений с обратной связью e.
Для следующей системы пространства состояний с объектом с увеличенным интегратором:
Проблемные данные должны удовлетворить:
Пара (Aa, Ba) stabilizable.
R> 0 и .
не имеет никакого неразличимого режима на мнимой оси (или модульный круг в дискретное время).
lqi поддерживает модели дескриптора с несингулярным E. Вывод S lqi является решением уравнения Riccati для эквивалентной явной модели в пространстве состояний
[1] П. К. Янг и Дж. К. Виллемс, “Подход к линейной многомерной проблеме сервомеханизма”, Международный журнал Управления, Объем 15, Выпуск 5, май 1972, страницы 961-979.