Можно использовать функцию smooth, чтобы сглаживать данные об ответе. Можно использовать дополнительные методы для скользящего среднего значения, фильтров Savitzky-Golay и локальной регрессии с и без весов и робастности (lowess, loess, rlowess и rloess).
Фильтр скользящего среднего значения сглаживает данные, заменяя каждую точку данных на среднее значение соседних точек данных, заданных в промежутке. Этот процесс эквивалентен lowpass, фильтрующему с ответом сглаживания, данного разностным уравнением
где ys (i) является сглаживавшим значением для i th точка данных, N является количеством соседних точек данных по обе стороны от ys (i), и 2N+1 промежуток.
Метод сглаживания скользящего среднего значения, используемый Curve Fitting Toolbox™, следует этим правилам:
Промежуток должен быть нечетным.
Точка данных, которая будет сглаживаться, должна находиться в центре промежутка.
Промежуток настроен для точек данных, которые не могут разместить конкретное количество соседей с обеих сторон.
Конечные точки не сглаживаются, потому что промежуток не может быть задан.
Обратите внимание на то, что можно использовать функцию filter, чтобы реализовать разностные уравнения такой как один показанный выше. Однако из-за способа, которым обработаны конечные точки, результат скользящего среднего значения тулбокса будет отличаться от результата, возвращенного filter. Обратитесь к Разностным уравнениям и Фильтрации (MATLAB) для получения дополнительной информации.
Например, предположите, что вы сглаживаете данные с помощью фильтра скользящего среднего значения с промежутком 5. Используя правила, описанные выше, первыми четырьмя элементами y s дают
ys(1) = y(1) ys(2) = (y(1)+y(2)+y(3))/3 ys(3) = (y(1)+y(2)+y(3)+y(4)+y(5))/5 ys(4) = (y(2)+y(3)+y(4)+y(5)+y(6))/5
Обратите внимание на то, что y s(1), y s(2)..., y s(end) относится к порядку данных после сортировки, и не обязательно первоначального заказа.
Сглаживавшие значения и промежутки для первых четырех точек данных сгенерированного набора данных показывают ниже.
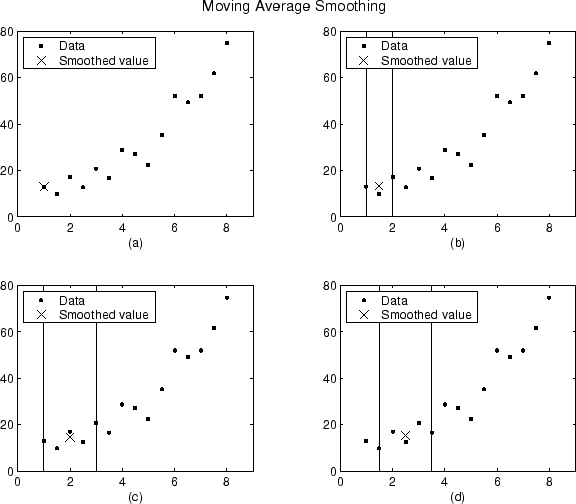
Постройте (a), указывает, что точка First Data не сглаживается, потому что промежуток не может быть создан. Постройте (b), указывает, что вторая точка данных сглаживается с помощью промежутка три. (c) графиков и (d) указывают, что промежуток пять используется, чтобы вычислить сглаживавшее значение.
Фильтрация Savitzky-Golay может считаться обобщенным скользящим средним значением. Вы выводите коэффициенты фильтра путем выполнения невзвешенной подгонки линейного метода наименьших квадратов использование полинома данной степени. Поэтому фильтр Savitzky-Golay также называется цифровым фильтром полинома сглаживания или наименьшие квадраты, сглаживающие фильтр. Обратите внимание на то, что более высокий полином степени позволяет достигнуть высокого уровня сглаживания без затухания функций данных.
Savitzky-Golay фильтрация метода часто используется с данными о частоте или со спектроскопическими (пиковыми) данными. Для данных о частоте метод является эффективным при сохранении высокочастотных компонентов сигнала. Для спектроскопических данных метод является эффективным при сохранении более высоких моментов пика, таких как ширина линии. Для сравнения фильтр скользящего среднего значения имеет тенденцию отфильтровывать значительный фрагмент высокочастотного содержимого сигнала, и это может только сохранить более низкие моменты пика, такие как центроид. Однако фильтрация Savitzky-Golay может быть менее успешной, чем фильтр скользящего среднего значения при отклонении шума.
Savitzky-Golay сглаживание метода, используемого программным обеспечением Curve Fitting Toolbox, следует этим правилам:
Промежуток должен быть нечетным.
Полиномиальная степень должна быть меньше, чем промежуток.
Точки данных не требуются, чтобы иметь универсальный интервал.
Обычно, фильтрация Savitzky-Golay требует универсального интервала данных о предикторе. Однако алгоритм Curve Fitting Toolbox поддерживает неоднородный интервал. Поэтому вы не обязаны выполнять дополнительный шаг фильтрации, чтобы создать данные с универсальным интервалом.
График, показанный ниже отображений, сгенерировал Гауссовы данные и несколько попыток сглаживания использования метода Savitzky-Golay. Данные являются очень шумными, и пиковые ширины отличаются от широко, чтобы сузиться. Промежуток равен 5% количества точек данных.
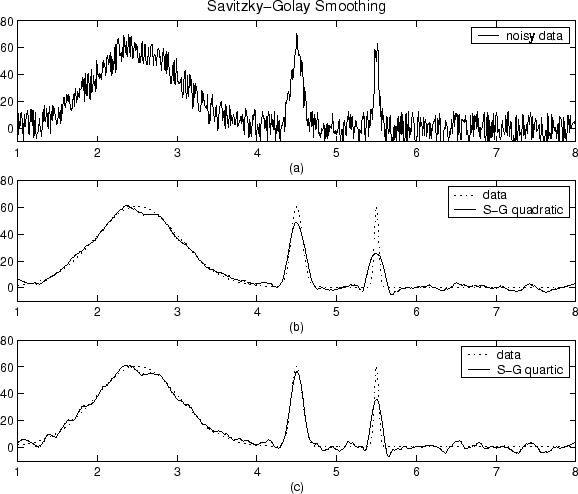
График (a) показывает шумные данные. Чтобы более легко сравнить сглаживавшие результаты, (b) графиков и (c) показывают данные без добавленного шума.
График (b) показывает результат сглаживания с квадратичным полиномом. Заметьте, что метод выполняет плохо для узкого peaks. График (c) показывает результат сглаживания с биквадратным полиномом. В целом более высокие полиномы степени могут более точно получить высоты и ширины узкого peaks, но могут сделать плохо при сглаживании более широкого peaks.
Имена “lowess” и “лесс” выведены от термина, “локально взвесил сглаженный график рассеивания”, как оба использования методов локально взвешенная линейная регрессия, чтобы сглаживать данные.
Процесс сглаживания рассматривается локальным, потому что, как метод скользящего среднего значения, каждое сглаживавшее значение определяется путем граничения с точками данных, заданными в промежутке. Процесс взвешивается, потому что функция веса регрессии задана для точек данных, содержавших в промежутке. В дополнение к функции веса регрессии можно использовать устойчивую функцию веса, которая делает процесс стойким к выбросам. Наконец, методы дифференцируются моделью, используемой в регрессии: lowess использует линейный полином, в то время как лесс использует квадратичный полином.
Локальные методы сглаживания регрессии, используемые программным обеспечением Curve Fitting Toolbox, следуют этим правилам:
Промежуток может быть даже или нечетен.
Можно задать промежуток как процент общего количества точек данных в наборе данных. Например, промежуток 0,1 использования 10% точек данных.
Локальный процесс сглаживания регрессии выполняет эти шаги для каждой точки данных:
Вычислите веса регрессии для каждой точки данных в промежутке. Веса даны функцией tricube, показанной ниже.
x является значением предиктора, сопоставленным со значением ответа, которое будет сглаживаться, xi самые близкие соседи x, как задано промежутком, и d (x) является расстоянием вдоль абсциссы от x до самого удаленного значения предиктора в промежутке. Веса имеют эти характеристики:
Точка данных, которая будет сглаживаться, имеет самый большой вес и большую часть влияния на подгонку.
Точки данных вне промежутка имеют нулевой вес и никакое влияние на подгонку.
Выполняется взвешенная регрессия линейного метода наименьших квадратов. Для lowess регрессия использует первый полином степени. Для лесса регрессия использует второй полином степени.
Сглаживавшее значение дано взвешенной регрессией в значении предиктора интереса.
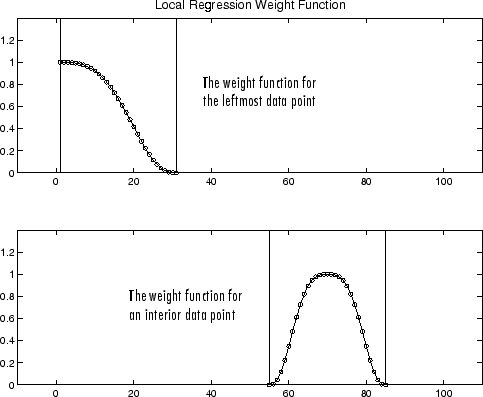
Если сглаженное вычисление включает то же количество соседних точек данных по обе стороны от сглаживавшей точки данных, функция веса симметрична. Однако, если количество соседних точек не симметрично о сглаживавшей точке данных, то функция веса не симметрична. Обратите внимание на то, что различающийся процесс сглаживания скользящего среднего значения, промежуток никогда не изменяется. Например, когда вы сглаживаете точку данных с наименьшим значением предиктора, форма функции веса является усеченной одной половиной, крайняя левая точка данных в промежутке имеет самый большой вес, и все соседние точки справа от сглаживавшего значения.
Функцию веса для конечной точки и для внутренней точки показывают ниже для промежутка 31 точки данных.
Используя lowess метод с промежутком пять, сглаживавшие значения и сопоставленные регрессии для первых четырех точек данных сгенерированного набора данных показывают ниже.
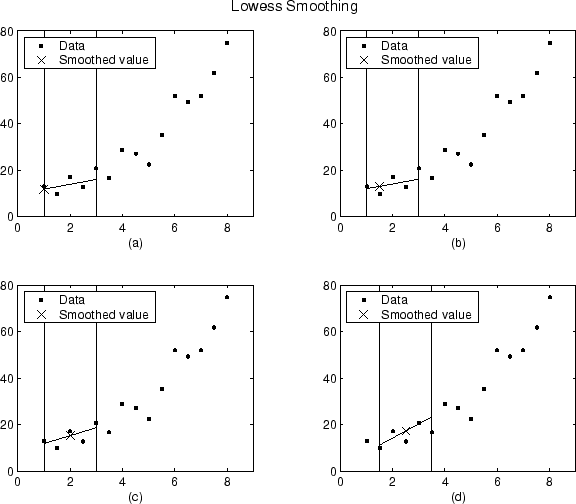
Заметьте, что промежуток не изменяется, в то время как процесс сглаживания прогрессирует от точки данных до точки данных. Однако в зависимости от количества самых близких соседей, вес регрессии функциональная сила не быть симметричным о точке данных, которая будет сглаживаться. В частности, строит (a), и (b) используют асимметричную функцию веса, в то время как графики (c) и (d) используют симметричную функцию веса.
Для метода лесса графики выглядели бы одинаково кроме сглаживавшего значения, будет сгенерирован полиномом второй степени.
Если ваши данные содержат выбросы, сглаживавшие значения могут стать искаженными и не отразить поведение объема соседних точек данных. Чтобы преодолеть эту проблему, можно сглаживать данные с помощью устойчивой процедуры, которая не является под влиянием небольшой части выбросов. Для описания выбросов обратитесь к Остаточному Анализу.
Программное обеспечение Curve Fitting Toolbox обеспечивает устойчивую версию и для lowess и для методов сглаживания лесса. Эти устойчивые методы включают дополнительное вычисление устойчивых весов, которое является стойким к выбросам. Устойчивая процедура сглаживания выполняет эти шаги:
Вычислите невязки из процедуры сглаживания, описанной в предыдущем разделе.
Вычислите устойчивые веса для каждой точки данных в промежутке. Веса даны функцией bisquare,
где ri является невязкой i th точка данных, произведенная процедурой сглаживания регрессии, и MAD является средним абсолютным отклонением невязок,
Среднее абсолютное отклонение является мерой того, насколько распространенный невязки. Если ri является маленьким по сравнению с 6MAD, то устойчивый вес близко к 1. Если ri больше, чем 6MAD, устойчивый вес 0, и связанная точка данных исключена из сглаженного вычисления.
Сглаживайте данные снова с помощью устойчивых весов. Сглаживавшее значение финала вычисляется с помощью и локального веса регрессии и устойчивого веса.
Повторите предыдущие два шага для в общей сложности пяти итераций.
Результаты сглаживания lowess процедуры сравнены ниже с результатами устойчивой lowess процедуры для сгенерированного набора данных, который содержит один выброс. Промежуток для обеих процедур является 11 точками данных.
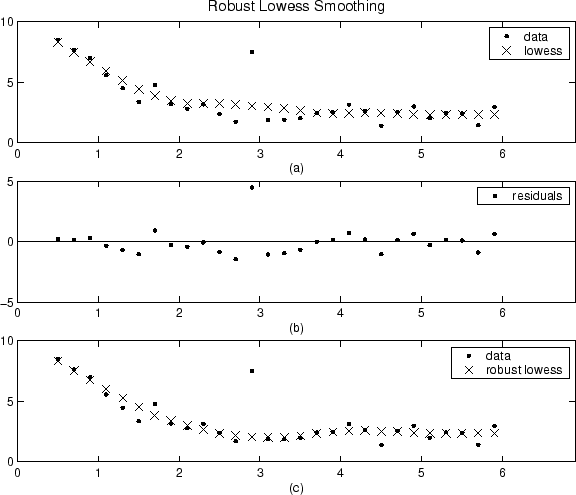
(a) графика показывает, что выброс влияет на сглаживавшее значение для нескольких самых близких соседей. (b) графика предполагает, что невязка выброса больше, чем шесть средних абсолютных отклонений. Поэтому устойчивый вес является нулем для этой точки данных. (c) графика показывает, что сглаживавшие значения, граничащие с выбросом, отражают объем данных.
Загрузите данные в count.dat:
load count.dat
24 3 массив count содержит количества трафика на трех пересечениях в течение каждого часа дня.
Во-первых, используйте фильтр скользящего среднего значения с 5-часовым промежутком, чтобы сглаживать все данные целиком (линейным индексом):
c = smooth(count(:)); C1 = reshape(c,24,3);
Отобразите на графике исходные данные и сглаживавшие данные:
subplot(3,1,1)
plot(count,':');
hold on
plot(C1,'-');
title('Smooth C1 (All Data)')Во-вторых, используйте тот же фильтр, чтобы сглаживать каждый столбец данных отдельно:
C2 = zeros(24,3);
for I = 1:3,
C2(:,I) = smooth(count(:,I));
endСнова, отобразите на графике исходные данные и сглаживавшие данные:
subplot(3,1,2)
plot(count,':');
hold on
plot(C2,'-');
title('Smooth C2 (Each Column)')Постройте различие между двумя сглаживавшими наборами данных:
subplot(3,1,3)
plot(C2 - C1,'o-')
title('Difference C2 - C1')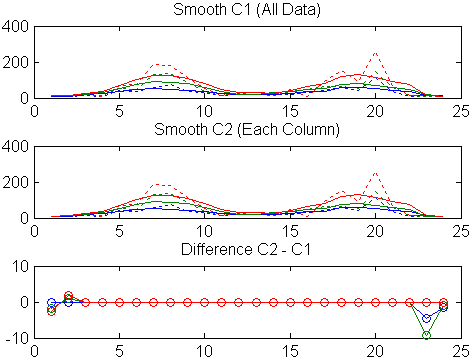
Отметьте дополнительные эффекты конца в сглаженном с 3 столбцами.
Создайте шумные данные с выбросами:
x = 15*rand(150,1); y = sin(x) + 0.5*(rand(size(x))-0.5); y(ceil(length(x)*rand(2,1))) = 3;
Сглаживайте данные с помощью loess и методов rloess с промежутком 10%:
yy1 = smooth(x,y,0.1,'loess'); yy2 = smooth(x,y,0.1,'rloess');
Отобразите на графике исходные данные и сглаживавшие данные.
[xx,ind] = sort(x);
subplot(2,1,1)
plot(xx,y(ind),'b.',xx,yy1(ind),'r-')
set(gca,'YLim',[-1.5 3.5])
legend('Original Data','Smoothed Data Using ''loess''',...
'Location','NW')
subplot(2,1,2)
plot(xx,y(ind),'b.',xx,yy2(ind),'r-')
set(gca,'YLim',[-1.5 3.5])
legend('Original Data','Smoothed Data Using ''rloess''',...
'Location','NW')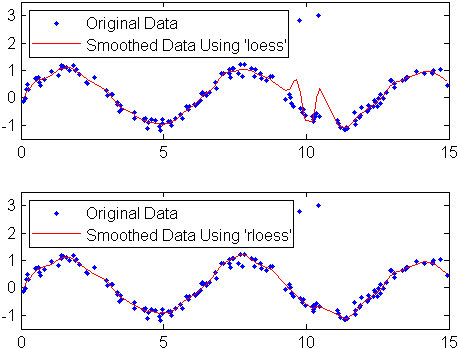
Обратите внимание на то, что выбросы имеют меньше влияния на устойчивый метод.