Этот пример иллюстрирует, как использовать недостающие алгоритмы данных для оптимизации портфеля и для оценки. Этот пример работает с пятью годами ежедневных данных о совокупном доходе для 12 запасов компьютерной технологии с 6 оборудованием и 6 компаниями-разработчиками программного обеспечения. Пример оценивает среднюю и ковариационную матрицу для этих запасов, формирует границы эффективности и с наивным подходом и с подходом ECM, и сравнивает результаты.
Можно запустить пример непосредственно с ecmtechdemo.m.
Загрузите следующий файл данных:
load ecmtechdemo
Этот файл содержит эти три количества:
Assets является массивом ячеек тикеров для этих 12 запасов в примере.
Data является 1254-by-12 матрица 1 254 ежедневных совокупных доходов для каждого из этих 12 запасов.
Dates является 1254-by-1 вектор-столбец дат, сопоставленных с данными.
Период времени для данных расширяет с 19 апреля 2000 до 18 апреля 2005.
Шестым запасом в Assets является Google (GOOG), который начал торговать 19 августа 2004. Так, все возвращается, до 20 августа 2004 отсутствуют и представленные как NaNs. Кроме того, Amazon (AMZN) имел несколько дней с отсутствующими значениями, рассеянными в течение прошлых пяти лет.
Наивный подход к оценке среднего значения и ковариации для этих 12 активов должен устранить все дни, которые имеют отсутствующие значения для любого из этих 12 активов. Используйте функциональный ecmninit с опцией nanskip, чтобы сделать это.
[NaNMean, NaNCovar] = ecmninit(Data,'nanskip');
Контрастируйте результат этого подхода с использованием всех доступных данных и функционального ecmnmle, чтобы вычислить среднее значение и ковариацию. Во-первых, вызовите ecmnmle без выходных аргументов, чтобы установить, что достаточно данных доступно, чтобы получить значимые оценки.
ecmnmle(Data);
Следующие данные показывают, что, даже почти с 87% данных Google, являющихся значениями NaN, алгоритм сходится только после четырех итераций.
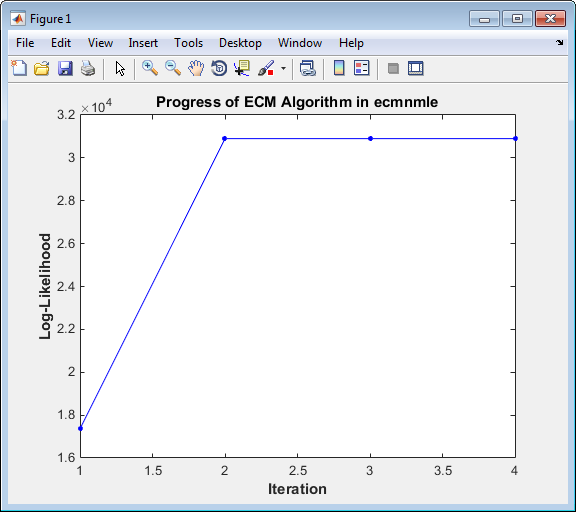
Оцените среднее значение и ковариацию, как вычислено ecmnmle.
[ECMMean, ECMCovar] = ecmnmle(Data)
ECMMean =
0.0008
0.0008
-0.0005
0.0002
0.0011
0.0038
-0.0003
-0.0000
-0.0003
-0.0000
-0.0003
0.0004
ECMCovar =
0.0012 0.0005 0.0006 0.0005 0.0005 0.0003
0.0005 0.0024 0.0007 0.0006 0.0010 0.0004
0.0006 0.0007 0.0013 0.0007 0.0007 0.0003
0.0005 0.0006 0.0007 0.0009 0.0006 0.0002
0.0005 0.0010 0.0007 0.0006 0.0016 0.0006
0.0003 0.0004 0.0003 0.0002 0.0006 0.0022
0.0005 0.0005 0.0006 0.0005 0.0005 0.0001
0.0003 0.0003 0.0004 0.0003 0.0003 0.0002
0.0006 0.0006 0.0008 0.0007 0.0006 0.0002
0.0003 0.0004 0.0005 0.0004 0.0004 0.0001
0.0005 0.0006 0.0008 0.0005 0.0007 0.0003
0.0006 0.0012 0.0008 0.0007 0.0011 0.0016
ECMCovar (continued)
0.0005 0.0003 0.0006 0.0003 0.0005 0.0006
0.0005 0.0003 0.0006 0.0004 0.0006 0.0012
0.0006 0.0004 0.0008 0.0005 0.0008 0.0008
0.0005 0.0003 0.0007 0.0004 0.0005 0.0007
0.0005 0.0003 0.0006 0.0004 0.0007 0.0011
0.0001 0.0002 0.0002 0.0001 0.0003 0.0016
0.0009 0.0003 0.0005 0.0004 0.0005 0.0006
0.0003 0.0005 0.0004 0.0003 0.0004 0.0004
0.0005 0.0004 0.0011 0.0005 0.0007 0.0007
0.0004 0.0003 0.0005 0.0006 0.0004 0.0005
0.0005 0.0004 0.0007 0.0004 0.0013 0.0007
0.0006 0.0004 0.0007 0.0005 0.0007 0.0020
Учитывая оценки для среднего значения и ковариации актива возвращается выведенный из наивного и подходов ECM, оценочных портфелей, и сопоставленных ожидаемых доходов и рисков на границе эффективности для обоих подходов.
[ECMRisk, ECMReturn, ECMWts] = portopt(ECMMean',ECMCovar,10); [NaNRisk, NaNReturn, NaNWts] = portopt(NaNMean',NaNCovar,10);
Постройте результаты на том же графике, чтобы проиллюстрировать различия.
figure(gcf) plot(ECMRisk,ECMReturn,'-bo','MarkerFaceColor','b','MarkerSize', 3); hold on plot(NaNRisk,NaNReturn,'-ro','MarkerFaceColor','r','MarkerSize', 3); title('\bfEfficient Frontiers under Various Assumptions'); legend('ECM','NaN','Location','SouthEast'); xlabel('\bfStd. Dev. of Returns'); ylabel('\bfMean of Returns'); hold off
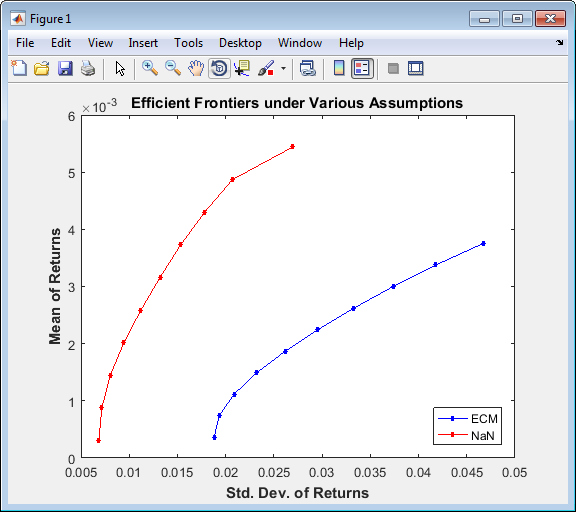
Безусловно, наивный подход оптимистичен относительно компромиссов возврата риск для этой вселенной 12 технологических акций. Доказательство, однако, находится в весах портфеля. Чтобы просмотреть веса, войти
Assets ECMWts NaNWts
который генерирует
>> Assets
ans =
'AAPL' 'AMZN' 'CSCO' 'DELL' 'EBAY' 'GOOG'
>> ECMWts
ans =
0.0358 0.0011 -0.0000 0.0000 0.0000 0.0989
0.0654 0.0110 0.0000 0.0000 0.0000 0.1877
0.0923 0.0194 0.0000 0.0000 0.0000 0.2784
0.1165 0.0264 0.0000 -0.0000 0.0000 0.3712
0.1407 0.0334 -0.0000 0 0.0000 0.4639
0.1648 0.0403 0.0000 0 -0.0000 0.5566
0.1755 0.0457 0.0000 -0.0000 -0.0000 0.6532
0.1845 0.0509 0.0000 0.0000 -0.0000 0.7502
0.1093 0.0174 -0.0000 0.0000 0 0.8733
0 0 -0.0000 0.0000 0 1.0000
>> NaNWts
ans =
-0.0000 0.0000 -0.0000 0.1185 0.0000 0.0522
0.0576 -0.0000 -0.0000 0.1219 0.0000 0.0854
0.1248 -0.0000 -0.0000 0.0952 -0.0000 0.1195
0.1969 -0.0000 -0.0000 0.0529 -0.0000 0.1551
0.2690 -0.0000 -0.0000 0.0105 0.0000 0.1906
0.3414 0.0000 -0.0000 -0.0000 -0.0000 0.2265
0.4235 0.0000 -0.0000 -0.0000 -0.0000 0.2639
0.5245 0.0000 -0.0000 -0.0000 -0.0000 0.3034
0.6269 -0.0000 -0.0000 -0.0000 -0.0000 0.3425
1.0000 -0.0000 -0.0000 0.0000 -0.0000 0
Assets (continued)
'HPQ' 'IBM' 'INTC' 'MSFT' 'ORCL' 'YHOO'
ECMWts (continued)
0.0535 0.4676 0.0000 0.3431 -0.0000 0.0000
0.0179 0.3899 -0.0000 0.3282 0.0000 -0.0000
0 0.3025 -0.0000 0.3074 0.0000 -0.0000
0.0000 0.2054 -0.0000 0.2806 0.0000 0.0000
0.0000 0.1083 -0.0000 0.2538 -0.0000 0.0000
0.0000 0.0111 -0.0000 0.2271 -0.0000 0.0000
0.0000 0.0000 -0.0000 0.1255 -0.0000 0.0000
0.0000 0 -0.0000 0.0143 -0.0000 -0.0000
0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000
0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000
NaNWts (continued)
0.0824 0.1779 0.0000 0.5691 -0.0000 0.0000
0.1274 0.0460 0.0000 0.5617 -0.0000 -0.0000
0.1674 -0.0000 0.0000 0.4802 0.0129 -0.0000
0.2056 -0.0000 0.0000 0.3621 0.0274 -0.0000
0.2438 -0.0000 0.0000 0.2441 0.0419 -0.0000
0.2782 -0.0000 0.0000 0.0988 0.0551 -0.0000
0.2788 -0.0000 0.0000 -0.0000 0.0337 -0.0000
0.1721 -0.0000 0.0000 -0.0000 -0.0000 -0.0000
0.0306 -0.0000 0.0000 0.0000 0 -0.0000
0 0.0000 0.0000 -0.0000 -0.0000 -0.0000
Наивные портфели в NaNWts имеют тенденцию способствовать Apple Computer (AAPL), который, оказалось, преуспел за период от Google IPO в конец периода оценки, в то время как портфели ECM в ECMWts склоняются к весящей ниже нормы Apple Computer и рекомендовать увеличенные веса в Google относительно наивных весов.
Оценивать влияние ошибки оценки и, в частности, эффект недостающих данных, ecmnstd использования, чтобы вычислить стандартные погрешности. Несмотря на то, что возможно оценить стандартные погрешности и для среднего значения и для ковариации, стандартные погрешности для одних только средних оценок обычно являются основными количествами интереса.
StdMeanF = ecmnstd(Data,ECMMean,ECMCovar,'fisher');
Вычислите стандартные погрешности, которые используют сгенерированную данными матрицу Гессиана (который составляет возможную потерю информации из-за недостающих данных) с опцией HESSIAN.
StdMeanH = ecmnstd(Data,ECMMean,ECMCovar,'hessian');
Различие в стандартных погрешностях показывает увеличение неуверенности в оценке ожидаемых доходов актива из-за недостающих данных. Это может быть просмотрено путем ввода:
Assets StdMeanH' StdMeanF' StdMeanH' - StdMeanF'
Эти два актива с missing data, AMZN и GOOG, являются единственными активами, чтобы разойтись во мнениях из-за недостающей информации.
convert2sur | ecmlsrmle | ecmlsrobj | ecmmvnrfish | ecmmvnrfish | ecmmvnrmle | ecmmvnrobj | ecmmvnrstd | ecmmvnrstd | ecmnfish | ecmnhess | ecmninit | ecmnmle | ecmnobj | ecmnstd | mvnrfish | mvnrmle | mvnrobj | mvnrstd