Что такое Sugeno-тип нечеткий вывод?

Эта тема обсуждает Sugeno, или Такаги-Суджено-Канга, метод нечеткого вывода. Введенный в 1 985 [1], этот метод подобен методу Mamdani во многих отношениях. Первые две части нечеткого процесса вывода, fuzzifying входные параметры и применение нечеткого оператора, являются тем же самым. Основное различие между Mamdani и Sugeno - то, что Sugeno функции принадлежности вывода является или линейным или постоянным.

Типичное правило в Sugeno нечеткая модель имеет форму:

Если Введено 1 x, и Входом 2 является y, то Выводом является z = a x + b y + c

Для нулевого порядка модель Sugeno уровень на выходе z является константой (a = b = 0).

Каждое правило взвешивает свой уровень на выходе, z _i, силой увольнения правила, w _i. Например, для правила AND с Входом 1 = x и Вход 2 = y, сила увольнения

$w_{i} = A n d M e t h o d (F_{1} (x), F_{2} (y))$

где F _1,2(.) является функциями принадлежности для Входных параметров 1 и 2.

Окончательный результат системы является взвешенным средним всего правила выходные параметры, вычисленные как

$Окончательный результат = \frac{\sum_{i =1}^{N} w_{i} z_{i}}{\sum_{i = 1}^{N} w_{i}}$

где N является количеством правил.

Правило Sugeno действует как показано в следующей схеме.

Примечание

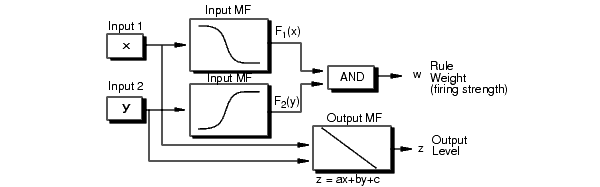
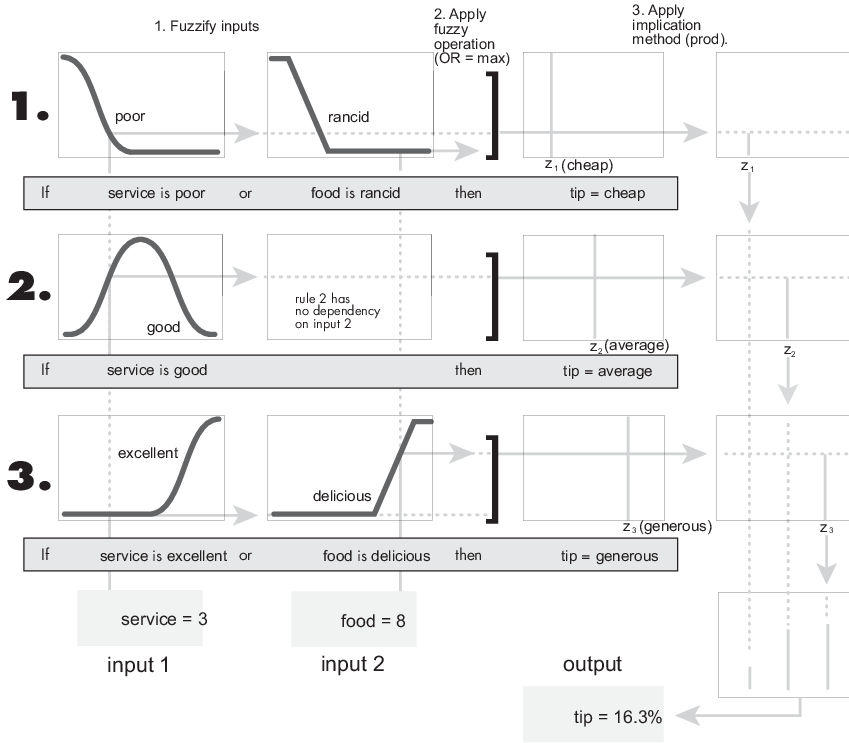
Системы Sugeno всегда используют значение продукта и суммируют агрегацию.

Предыдущие данные показывают нечеткую модель добавления подсказки, разработанную в Нечетком Процессе Вывода, адаптированном к использованию в качестве системы Sugeno. К счастью, часто имеет место, что одноэлементные выходные функции достаточны для потребностей данной проблемы. Как пример, система tippersg.fis является представлением Sugeno-типа теперь знакомой модели добавления подсказки. Если вы загружаете систему и строите ее выходную поверхность, вы видите, что это - почти то же самое как система Mamdani, которую вы ранее видели.

fis = readfis('tippersg');
gensurf(fis)

Самый легкий способ визуализировать системы Sugeno первого порядка состоит в том, чтобы думать о каждом правиле как об определении местоположения движущегося одиночного элемента. Таким образом, одноэлементные выходные скачки могут переместиться линейным способом на выходном пробеле, в зависимости от того, каков вход. Это также имеет тенденцию делать системное обозначение компактным и эффективным. Нечеткие модели Sugeno высшего порядка возможны, но они начинают значительную сложность с небольшой очевидной заслуги. Sugeno нечеткие модели, выходные функции принадлежности которых больше, чем первый порядок, не поддержаны программным обеспечением Fuzzy Logic Toolbox™.

Из-за линейной зависимости каждого правила о входных переменных метод Sugeno идеален для действия как супервизор интерполяции нескольких линейных контроллеров, которые должны быть применены, соответственно, к различным условиям работы динамической нелинейной системы. Например, производительность самолета может измениться существенно с высотой и Числом Маха. Линейные контроллеры, хотя легкий, чтобы вычислить и подходящий для любого данного условия рейса, должны обновляться регулярно и гладко не отставать от изменяющегося состояния автомобиля рейса. Нечеткая система вывода Sugeno подходит для задачи сглаженной интерполяции линейных усилений, которые были бы применены через входной пробел; это - естественный и эффективный планировщик усиления. Точно так же система Sugeno подходит для моделирования нелинейных систем путем интерполяции между несколькими линейными моделями.

Чтобы видеть определенный пример системы с линейными выходными функциями принадлежности, считайте систему с одним выходом, с одним входом сохраненной в sugeno1.fis. Загрузите систему и просмотрите свойства ее выходной переменной.

fis = readfis('sugeno1');
fis.Outputs(1)

ans = 
  fisvar with properties:

                   Name: "output"
                  Range: [0 1]
    MembershipFunctions: [1x2 fismf]

Выходная переменная имеет две функции принадлежности. Просмотрите свойства первой функции принадлежности.

fis.Outputs(1).MembershipFunctions(1)

ans = 
  fismf with properties:

          Name: "line1"
          Type: "linear"
    Parameters: [-1 -1]

Просмотрите свойства второй функции принадлежности.

fis.Outputs(1).MembershipFunctions(2)

ans = 
  fismf with properties:

          Name: "line2"
          Type: "linear"
    Parameters: [1 -1]

Далее, эти функции принадлежности являются линейными функциями входной переменной. Функция принадлежности line1 задана уравнением:

$o u t p u t = (- 1) \times i n p u t + (- 1)$

и функция принадлежности line2:

$o u t p u t = (1) \times i n p u t + (- 1)$

Входные функции принадлежности и правила задают, какая из этих выходных функций выражается и когда:

fis.Rules

ans = 
  1x2 fisrule array with properties:

    Description
    Antecedent
    Consequent
    Weight
    Connection

  Details:
                    Description           
         _________________________________

    1    "input==low => output=line1 (1)" 
    2    "input==high => output=line2 (1)"

Функциональный plotmf показывает нам, что функция принадлежности, low обычно отсылает к входным значениям меньше, чем нуль, в то время как high относится к значениям, больше, чем нуль. Функциональный gensurf показывает, как полная нечеткая система выводила переключатели гладко от строки под названием line1 к строке под названием line2.

subplot(2,1,1)
plotmf(fis,'input',1)
subplot(2,1,2)
gensurf(fis)

Когда этот пример показывает, Sugeno-система-типов дает вам свободу включить линейные системы в ваши нечеткие системы. Следовательно, вы могли создать нечеткую систему, которая переключается между несколькими оптимальными линейными контроллерами, когда очень нелинейная система перемещается на ее операционном пробеле.

Ссылки

[1] Sugeno, M., Промышленное применение нечеткого управления, паба Elsevier Science. Ко., 1985.

Смотрите также

gensurf | readfis

Документация