Оцените и подтвердите нелинейные модели от single-input/single-output (SISO) данные, чтобы найти тот, который лучше всего представляет вашу системную динамику.
После завершения этого примера вы сможете выполнить следующие задачи с помощью приложения System Identification:
Импортируйте объекты данных из рабочей области MATLAB® в приложение.
Оцените и подтвердите нелинейные модели от данных.
Постройте и анализируйте поведение нелинейности.
Этот пример использует файл данных twotankdata.mat, который содержит данные временного интервала SISO для системы 2D корпуса, показанной в следующей фигуре.
Система 2D корпуса
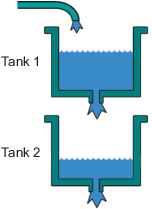
В системе 2D корпуса вода льется через канал в Корпус 1, стекает в Корпус 2 и оставляет систему через маленькое отверстие в нижней части Корпуса 2. Измеренный вход u (t) к системе является напряжением, применился к насосу, который подает воду в Корпус 1 (в вольтах). Измеренный вывод y (t) является высотой воды в более низком корпусе (в метрах).
На основе закона Бернулли, который утверждает, что вода, текущая через маленькое отверстие в нижней части корпуса, зависит нелинейно на уровне воды в корпусе, вы ожидаете, что отношение между входом и выходными данными будет нелинейно.
twotankdata.mat включает 3 000 выборок с шагом расчета 0,2 с.
Можно оценить нелинейные модели черного ящика дискретного времени и для одно вывода и для нескольких - выходные данные временного интервала. Можно выбрать из двух типов нелинейных, структур модели черного ящика:
Нелинейные модели ARX
Хаммерстайн-Винер моделирует
Можно оценить модели черного ящика Хаммерстайна-Винера от данных о вводе/выводе только. Эти модели не поддерживают данные timeseries, где нет никакого входа.
Для получения дополнительной информации об оценке нелинейных моделей черного ящика смотрите Нелинейную Образцовую Идентификацию.
Нелинейная модель ARX состоит из образцовых регрессоров и средства оценки нелинейности. Средство оценки нелинейности включает и линейные и нелинейные функции, которые действуют на образцовые регрессоры, чтобы дать образцовый вывод. Эта блок-схема представляет структуру нелинейной модели ARX в сценарии симуляции.
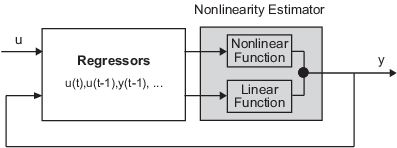
Программное обеспечение вычисляет нелинейную модель ARX вывод y на двух этапах:
Это вычисляет значения регрессора из текущих и прошлых входных значений и прошлых выходных данных.
В самом простом случае регрессоры являются задержанными вводами и выводами, такими как u (t-1) и y (t-3). Подобные регрессоры называются стандартными регрессорами. Вы задаете стандартные регрессоры с помощью порядков модели и задержки. Для получения дополнительной информации смотрите Нелинейные Порядки Модели ARX и Задержку. Можно также задать пользовательские регрессоры, которые являются нелинейными функциями задержанных вводов и выводов. Например, u (t-1) *y (t-3). Чтобы создать набор полиномиальных регрессоров типа, используйте polyreg.
По умолчанию все регрессоры являются входными параметрами и к линейному и к нелинейным функциональным блокам средства оценки нелинейности. Можно выбрать подмножество регрессоров как входные параметры к нелинейному функциональному блоку.
Это сопоставляет регрессоры с образцовым выводом с помощью блока средства оценки нелинейности. Блок средства оценки нелинейности может включать линейные и нелинейные блоки параллельно. Например:
Здесь, x является вектором регрессоров, и r является средним значением регрессоров x. вывод блока линейной функции и является аффинным когда d ≠ 0. d является скалярным смещением. представляет вывод нелинейного функционального блока. Q является матрицей проекции, которая делает вычисления хорошо подготовленными. Точная форма F (x) зависит от вашего выбора средства оценки нелинейности. Можно выбрать из доступных средств оценки нелинейности, таких как сети древовидного раздела, сети вейвлета и многоуровневые нейронные сети. Можно также исключить или линейное или нелинейный функциональный блок от средства оценки нелинейности.
При оценке нелинейной модели ARX программное обеспечение вычисляет значения параметра модели, такие как L, r, d, Q и другие параметры, задающие g.
Получившиеся нелинейные модели ARX являются объектами idnlarx, которые хранят все данные модели, включая образцовые регрессоры и параметры средства оценки нелинейности. Для получения дополнительной информации об этих объектах, смотрите Нелинейные Образцовые Структуры.
Эта блок-схема представляет структуру модели Хаммерстайна-Винера:

Где,
f является нелинейной функцией, которая преобразовывает входные данные u (t) как w (t) = f (u (t)).
w (t), внутренняя переменная, является выводом блока Input Nonlinearity и имеет ту же размерность как u (t).
B/F является линейной передаточной функцией, которая преобразовывает w (t) как x (t) = (B/F) w (t).
x (t), внутренняя переменная, является выводом блока Linear и имеет ту же размерность как y (t).
B и F подобны полиномам в линейной модели Output-Error. Для получения дополнительной информации о моделях Output-Error, смотрите то, Что Полиномиальные Модели?.
Для ny выходные параметры и входные параметры nu, линейный блок является матрицей передаточной функции, содержащей записи:
где j = 1,2,...,ny и i = 1,2,...,nu.
h является нелинейной функцией, которая сопоставляет вывод линейного блока x (t) к системе вывод y (t) как y (t) = h (x (t)).
Поскольку действия f на входном порте линейного блока, эта функция вызвана входная нелинейность. Точно так же, потому что действия h на выходном порте линейного блока, эта функция вызвана выходная нелинейность. Если ваша система содержит несколько вводов и выводов, необходимо задать функции f и h для каждого сигнала ввода и вывода. Вы не должны включать и вход и выходную нелинейность в образцовой структуре. Когда модель содержит только входную нелинейность f, это называется моделью Hammerstein. Точно так же, когда модель содержит только выходную нелинейность h, это называется Винеровской моделью.
Программное обеспечение вычисляет модель Хаммерстайна-Винера вывод y на трех этапах:
Вычислите w (t) = f (u (t)) от входных данных.
w (t) является входом к линейной передаточной функции B/F.
Входная нелинейность является статической функцией (без памяти), где значение вывода данное время t зависит только от входного значения во время t.
Можно сконфигурировать входную нелинейность как сигмоидальную сеть, сеть вейвлета, насыщение, мертвую зону, кусочную линейную функцию, одномерный полином или пользовательскую сеть. Можно также удалить входную нелинейность.
Вычислите вывод линейного блока с помощью w (t) и начальные условия: x (t) = (B/F) w (t).
Можно сконфигурировать линейный блок путем определения порядков числителя B и знаменатель F.
Вычислите модель, выведенную путем преобразования вывода линейного блока x (t) с помощью нелинейного функционального h в качестве y (t) = h (x (t)).
Подобно входной нелинейности выходная нелинейность является статической функцией. Можно сконфигурировать выходную нелинейность таким же образом как входную нелинейность. Можно также удалить выходную нелинейность, такую что y (t) = x (t).
Получившиеся модели являются объектами idnlhw, которые хранят все данные модели, включая средства оценки нелинейности и параметры модели. Для получения дополнительной информации об этих объектах, смотрите Нелинейные Образцовые Структуры.
Загрузите выборочные данные в twotankdata.mat путем ввода следующей команды в Окне Команды MATLAB:
load twotankdata
Эта команда загружает следующие две переменные в браузер рабочего пространства MATLAB:
u является входными данными, который является напряжением, применился к насосу, который подает воду в Корпус 1 (в вольтах).
y является выходными данными, который является высотой воды в Корпусе 2 (в метрах).
Объекты данных System Identification Toolbox™ инкапсулируют и значения данных и свойства данных в одну сущность. Можно использовать команды System Identification Toolbox, чтобы удобно управлять этими объектами данных как одна сущности.
Вы, должно быть, уже загрузили выборочные данные в рабочее пространство MATLAB, как описано в Загрузке Данных в рабочее пространство MATLAB.
Используйте следующие команды, чтобы создать два объекта данных iddata, ze и zv, где ze содержит данные для образцовой оценки, и zv содержит данные для проверки допустимости модели. Ts является шагом расчета.
Ts = 0.2; % Sample time is 0.2 sec z = iddata(y,u,Ts); % First 1000 samples used for estimation ze = z(1:1000); % Remaining samples used for validation zv = z(1001:3000);
Чтобы просмотреть свойства объекта iddata, используйте команду get. Например:
get(ze)
Программное обеспечение MATLAB возвращает следующие свойства данных и значения:
Domain: 'Time'
Name: ''
OutputData: [1000x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [1000x1 double]
u: 'Same as InputData'
InputName: {'u1'}
InputUnit: {''}
Period: Inf
InterSample: 'zoh'
Ts: 0.2000
Tstart: 0.2000
SamplingInstants: [1000x0 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []Чтобы изменить свойства данных, используйте запись через точку. Например, чтобы присвоить названия канала и модули, которые подписывают оси графика, введите следующий синтаксис в Окне Команды MATLAB:
% Set time units to minutes ze.TimeUnit = 'sec'; % Set names of input channels ze.InputName = 'Voltage'; % Set units for input variables ze.InputUnit = 'V'; % Set name of output channel ze.OutputName = 'Height'; % Set unit of output channel ze.OutputUnit = 'm'; % Set validation data properties zv.TimeUnit = 'sec'; zv.InputName = 'Voltage'; zv.InputUnit = 'V'; zv.OutputName = 'Height'; zv.OutputUnit = 'm';
Чтобы проверить, что свойство InputName ze изменяется, введите следующую команду:
ze.inputname
Имена свойства, такие как InputName, не являются чувствительными к регистру. Можно также сократить имена свойства, которые запускаются с Input или Output путем заменения u Input и y для Output на имя свойства. Например, OutputUnit эквивалентен yunit.
Чтобы открыть приложение System Identification, введите следующую команду в Окне Команды MATLAB:
systemIdentification
Имя сеанса по умолчанию, Untitled, появляется в строке заголовка.
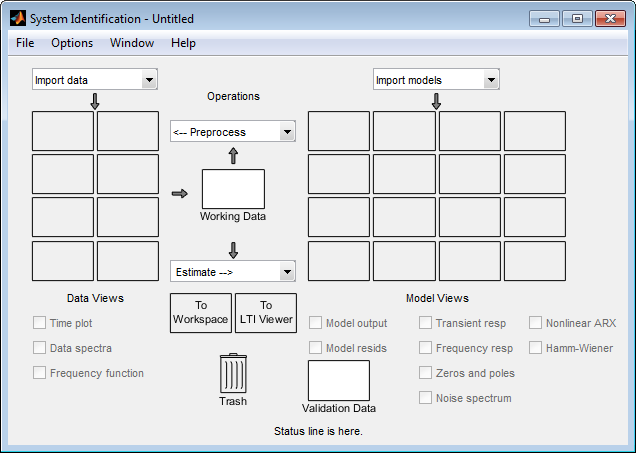
Можно импортировать объекты данных в приложение от рабочего пространства MATLAB.
Вы, должно быть, уже создали объекты данных, как описано в Создании iddata Объекты, и открыли приложение, как описано в Запуске Приложения System Identification.
Импортировать объекты данных:
В приложении System Identification выберите Import data> Data object.
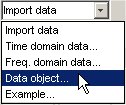
Это действие открывает диалоговое окно Import Data.
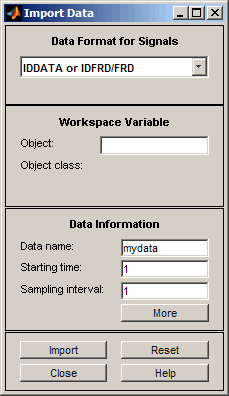
Введите ze в поле Object, чтобы импортировать данные об оценке. Нажмите Enter.
Это действие вводит информацию об объекте в Поля данных Импорта.
Нажмите More, чтобы просмотреть дополнительную информацию об этих данных, включая названия канала и модули.
Нажмите Import, чтобы добавить значок под названием ze к приложению System Identification.
В диалоговом окне Import Data введите zv в поле Object, чтобы импортировать данные о валидации. Нажмите Enter.
Нажмите Import, чтобы добавить значок под названием zv к приложению System Identification.
В диалоговом окне Import Data нажмите Close.
В приложении System Identification перетащите данные о валидации значок zv к прямоугольнику Validation Data. Данные об оценке значок ze уже определяются в прямоугольнике Working Data.
Также щелкните правой кнопкой по значку zv, чтобы открыть диалоговое окно Data/model Info. Установите флажок Use as Validation Data. Нажмите Apply и затем Close, чтобы добавить zv в прямоугольник Validation Data.
Приложение System Identification теперь напоминает следующую фигуру.
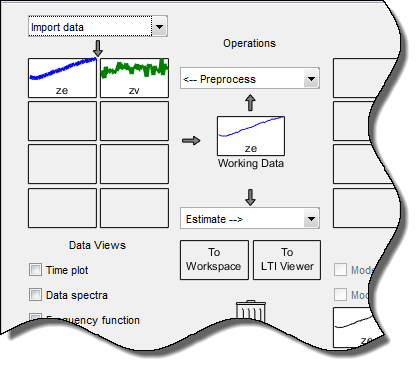
В этом фрагменте примера вы оцениваете нелинейную модель ARX с помощью образцовой структуры по умолчанию и опций оценки.
Вы, должно быть, уже подготовили данные, как описано в Подготовка данных. Для получения дополнительной информации о нелинейных моделях ARX, смотрите то, Что Нелинейная Модель ARX?
В приложении System Identification выберите Estimate> Nonlinear models.
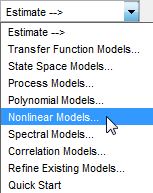
Это действие открывает диалоговое окно Nonlinear Models.
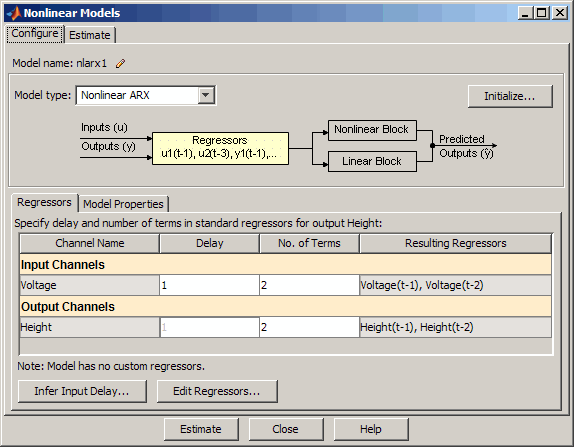
Вкладка Configure уже открыта, и Model type по умолчанию является Nonlinear ARX.
Во вкладке Regressors Input Channels и Output Channels установили Delay на 1 и набор No. of Terms к 2. Модель вывела y (t), связан с входом u (t) через следующее нелинейное авторегрессивное уравнение:
f является средством оценки нелинейности, выбранным в Nonlinearity выпадающий список вкладки Model Properties, и является Wavelet Network по умолчанию. Номер модулей для средства оценки нелинейности определяется к Select automatically и управляет гибкостью нелинейности — больше модулей соответствует более гибкой нелинейности.
Нажмите Estimate.
Это действие добавляет модель nlarx1 в приложение System Identification, как показано в следующей фигуре.
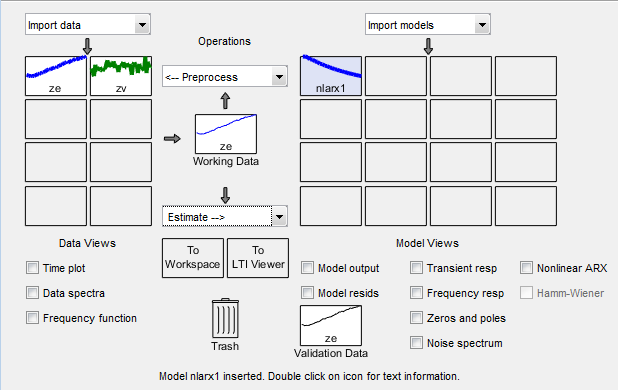
Диалоговое окно Nonlinear Models отображается сводные данные информации об оценке во вкладке Estimate. Fit (%) является среднеквадратичной погрешностью между результатами измерений и моделируемым выводом модели: 100% соответствуют совершенной подгонке (никакая ошибка) и 0% к модели, которая не способна к объяснению ни одного изменения вывода и только среднего уровня.
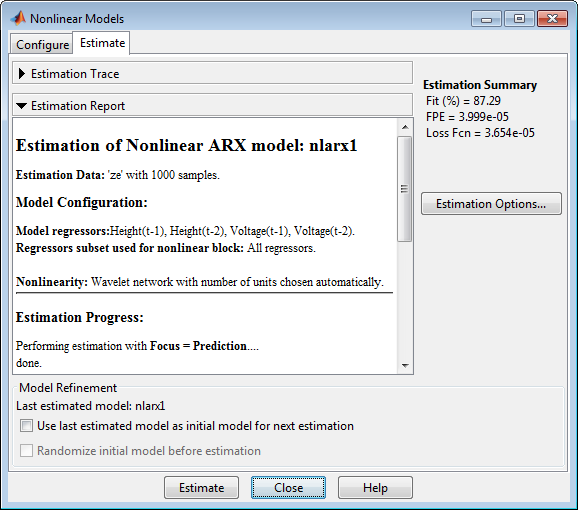
Fit (%) вычисляется с помощью набора данных оценки, а не набора данных валидации. Однако образцовый выходной график в следующем шаге сравнивает подгонку к набору данных валидации.
В приложении System Identification установите флажок Model output.
Это действие моделирует модель с помощью данных о контроле ввода, как введено для модели и строит моделируемый вывод сверху выходных данных о валидации.
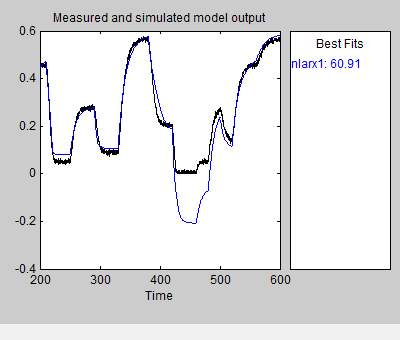
Область Best Fits Образцового Выходного графика показывает что соглашение между образцовым выводом и выводом данных валидации.
Выполните следующую процедуру, чтобы просмотреть форму нелинейности как функция регрессоров на Нелинейном графике Модели ARX.
В приложении System Identification установите флажок Nonlinear ARX , чтобы просмотреть поперечные сечения нелинейности.
По умолчанию график показывает отношение между выходными регрессорами Height(t-1) и Height(t-2). Этот график показывает регулярную плоскость в следующей фигуре. Таким образом отношение между регрессорами и выводом является приблизительно линейной плоскостью.
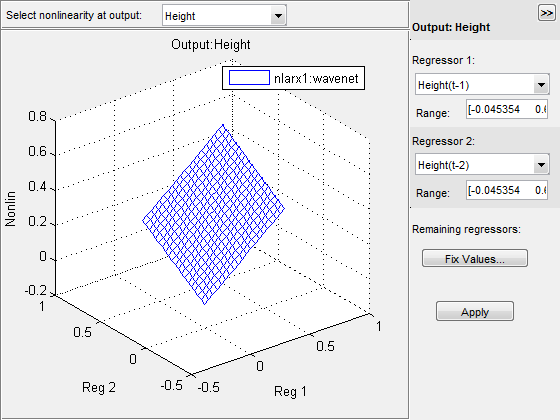
В окне Nonlinear ARX Model Plot, набор Regressor 1 к Voltage(t-1). Установите Regressor 2 на Voltage(t-2). Нажмите Apply.
Отношение между этими регрессорами и выводом нелинейно, как показано в следующем графике.
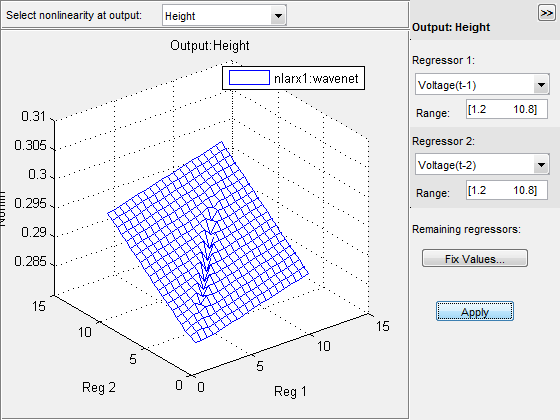
Чтобы вращать поверхность нелинейности, выберите Style> Rotate 3D и перетащите график к новой ориентации.
Чтобы отобразить 1D поперечное сечение для Регрессора 1, установите Регрессор 2 на none и нажмите Apply. Следующие данные показывают получившееся значение нелинейности для Регрессора 1, который представляет переключенный временем сигнал напряжения, Voltage(t-1).
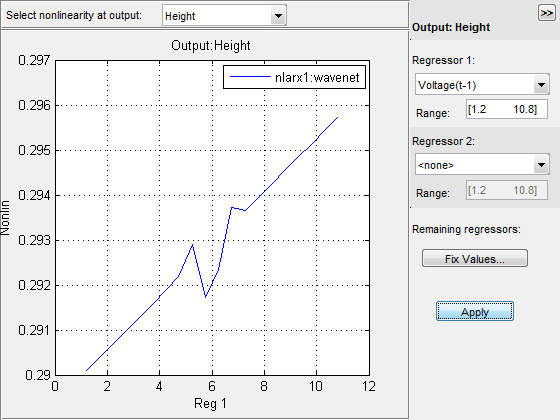
В этом фрагменте примера вы оцениваете нелинейную модель ARX с определенной входной задержкой и настройками нелинейности. Как правило, вы выбираете порядки модели методом проб и ошибок, пока вы не получаете модель, которая производит точную подгонку к данным.
Вы, должно быть, уже оценили нелинейную модель ARX с настройками по умолчанию, как описано в Оценке Нелинейной Модели ARX с Настройками по умолчанию.
В диалоговом окне Nonlinear Models кликните по вкладке Configure и кликните по вкладке Regressors.
Для канала входа Voltage дважды кликните соответствующую ячейку Delay, введите 3 и нажмите Enter.
Это действие обновляет список Resulting Regressors, чтобы показать Voltage(t-3), и Voltage(t-4) — называет с минимальной входной задержкой трех выборок.
Нажмите Estimate.
Это действие добавляет модель nlarx2 в приложение System Identification и обновляет Образцовое Окно вывода, чтобы включать эту модель. Диалоговое окно Nonlinear Models отображается новую информацию об оценке во вкладке Estimate.
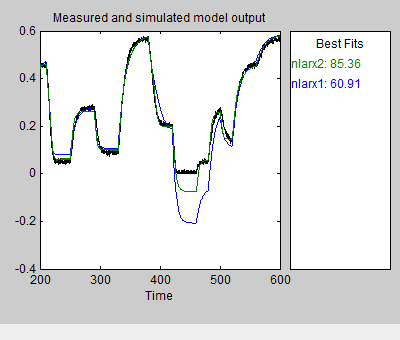
В диалоговом окне Nonlinear Models кликните по вкладке Configure и выберите вкладку Model Properties.
В области Number of units in nonlinear block выберите Enter и введите 6. Этот номер управляет гибкостью нелинейности.
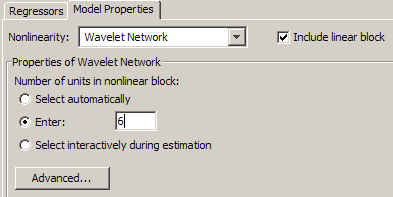
Нажмите Estimate.
Это действие добавляет модель nlarx3 в приложение System Identification. Это также обновляет Образцовое Окно вывода, как показано в следующей фигуре.
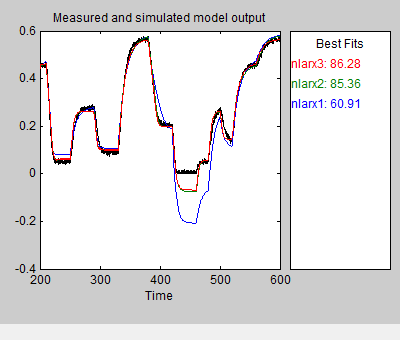
Можно оценить нелинейную модель ARX, которая включает только подмножество стандартных регрессоров, которые входят как входные параметры в нелинейный блок. По умолчанию все стандартные и пользовательские регрессоры используются в нелинейном блоке. В этом фрагменте примера вы только включаете стандартные регрессоры.
Вы, должно быть, уже задали образцовую структуру, как описано в Изменении Нелинейной Структуры Модели ARX.
В диалоговом окне Nonlinear Models кликните по вкладке Configure и выберите вкладку Regressors.
Нажмите кнопку Edit Regressors, чтобы открыть диалоговое окно Model Regressors.
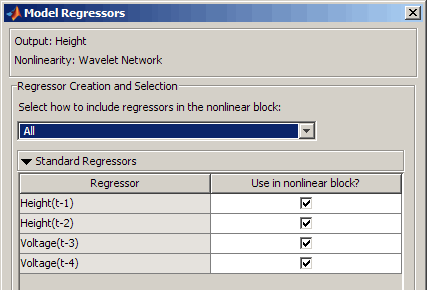
Снимите следующие флажки:
Height(t-2)
Voltage(t-3)
Нажмите OK.
Это действие исключает переключенный временем Height(t-2) и Voltage(t-3) из списка входных параметров к нелинейному блоку.
Нажмите Estimate.
Это действие добавляет модель nlarx4 в приложение System Identification. Это также обновляет Образцовое Окно вывода.
Можно оценить ряд нелинейных моделей ARX путем создания систематических изменений к образцовой структуре и основывать каждую новую модель на настройке ранее предполагаемой модели. В этом фрагменте примера вы оцениваете нелинейную модель ARX, которая подобна существующей модели (nlarx3), но с различной нелинейностью.
В диалоговом окне Nonlinear Models выберите вкладку Configure. Нажмите Initialize. Это действие открывает диалоговое окно Initial Model Specification.
В списке Initial Model выберите nlarx3. Нажмите OK.
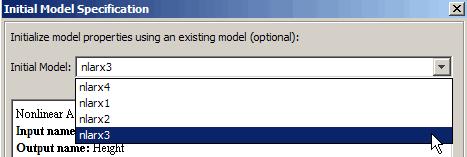
Кликните по вкладке Model Properties.
В списке Nonlinearity выберите Sigmoid Network.
В поле Number of units in nonlinear block введите 6.
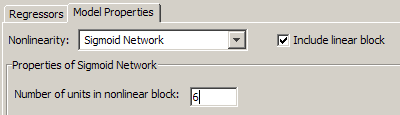
Нажмите Estimate.
Это действие добавляет модель nlarx5 в приложение System Identification. Это также обновляет Образцовый Выходной график, как показано в следующей фигуре.
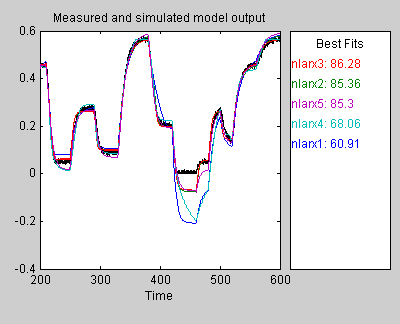
Лучшая модель является самой простой моделью, которая точно описывает динамику.
Чтобы просмотреть информацию о лучшей модели, включая порядок модели, нелинейность и список регрессоров, щелкают правой кнопкой по образцовому значку по приложению System Identification.
В этом фрагменте примера вы оцениваете нелинейные модели Хаммерстайна-Винера с помощью образцовой структуры по умолчанию и опций оценки.
Вы, должно быть, уже подготовили данные, как описано в Подготовка данных. Для получения дополнительной информации о нелинейных моделях ARX, смотрите то, Что Модель Хаммерстайна-Винера?
В приложении System Identification выберите Estimate> Nonlinear models, чтобы открыть диалоговое окно Nonlinear Models.
Во вкладке Configure выберите Hammerstein-Wiener в списке Model type.
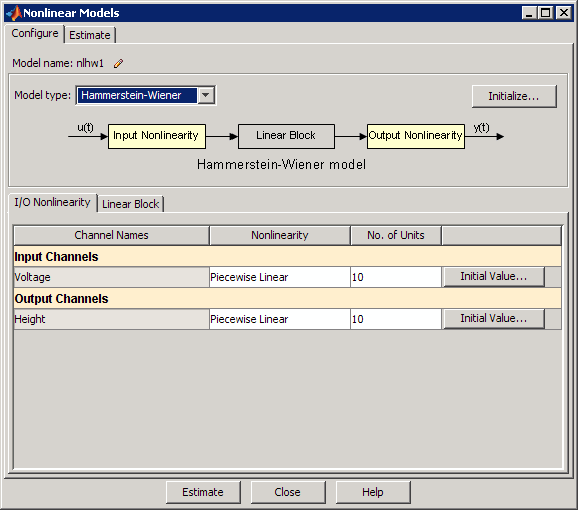
Вкладка I/O Nonlinearity открыта. Средством оценки нелинейности по умолчанию является Piecewise Linear с модулями 10 для Input Channels и Output Channels, который соответствует точкам останова 10 для кусочной линейной функции.
Выберите вкладку Linear Block, чтобы просмотреть порядки модели и ввести задержку.
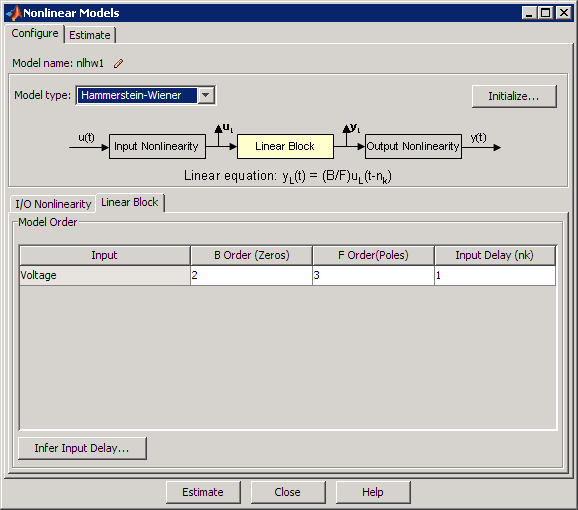
По умолчанию порядки модели и задержка линейной модели ошибки на выходе (OE) являются nb=2, nf=3, и nk=1.
Нажмите Estimate.
Это действие добавляет модель nlhw1 в приложение System Identification.
В приложении System Identification установите флажок Model output.
Это действие моделирует модель с помощью данных о контроле ввода, как введено для модели и строит моделируемый вывод сверху выходных данных о валидации.
Область Best Fits Образцового Окна вывода показывает соглашение между образцовым выводом и выводом данных валидации.
Можно построить нелинейность ввода/вывода и линейную передаточную функцию модели на графике Хаммерстайна-Винера.
В приложении System Identification установите флажок Hamm-Wiener, чтобы просмотреть график модели Хаммерстайна-Винера.
График отображает входную нелинейность, как показано в следующей фигуре.
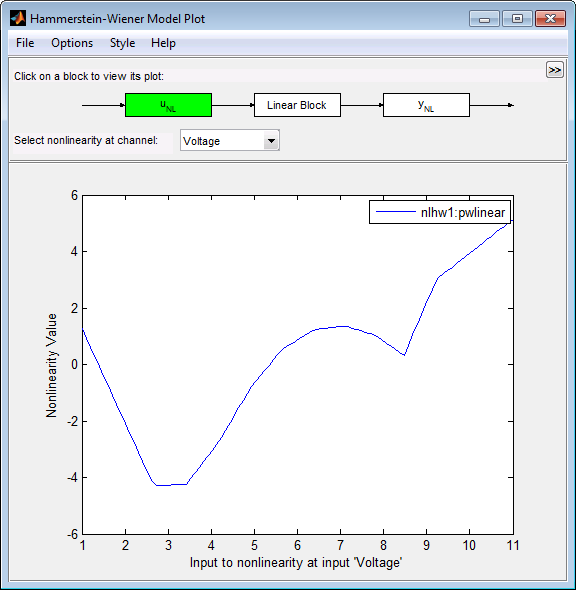
Кликните по yNL прямоугольнику в главном фрагменте окна Model Plot Хаммерстайна-Винера.
График обновляет, чтобы отобразить выходную нелинейность.
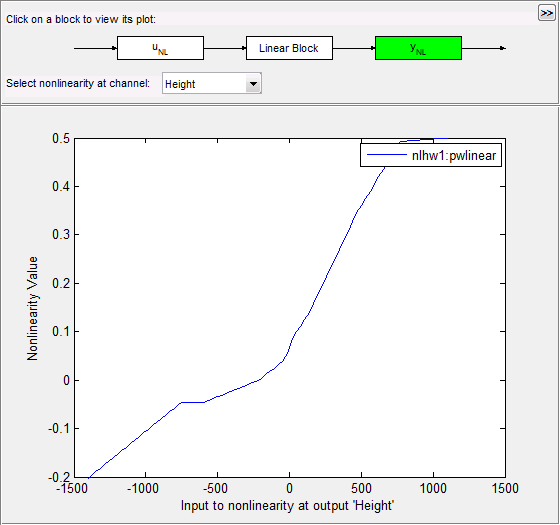
Кликните по прямоугольнику Linear Block в главном фрагменте окна Model Plot Хаммерстайна-Винера.
График обновляет, чтобы отобразить переходной процесс линейной передаточной функции.
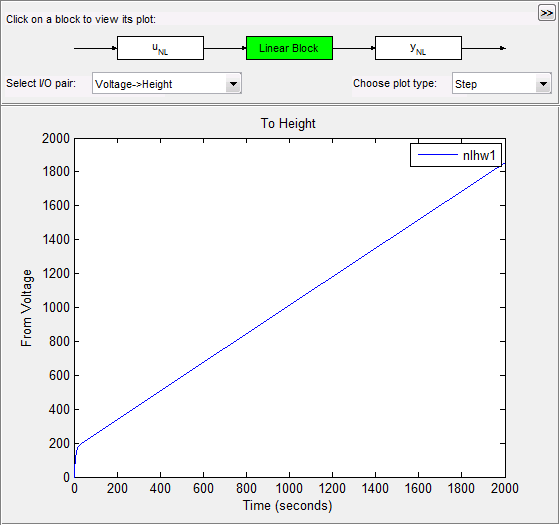
В списке Choose plot type выберите Bode. Это действие отображает Диаграмму Боде линейной передаточной функции.
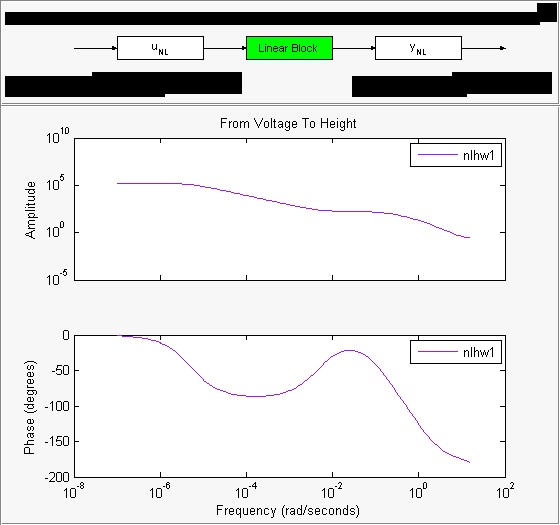
В этом фрагменте примера вы оцениваете модель Хаммерстайна-Винера с определенными образцовыми настройками порядка и нелинейности. Как правило, вы выбираете порядки модели и задержки методом проб и ошибок, пока вы не получаете модель, которая производит удовлетворительную подгонку к данным.
Вы, должно быть, уже оценили модель Хаммерстайна-Винера с настройками по умолчанию, как описано в Оценке Моделей Хаммерстайна-Винера с Настройками по умолчанию.
В диалоговом окне Nonlinear Models кликните по вкладке Configure и выберите вкладку Linear Block.
Для канала входа Voltage дважды кликните соответствующую ячейку Input Delay (nk), измените значение на 3 и нажмите Enter.
Нажмите Estimate.
Это действие добавляет модель nlhw2 в приложение System Identification, и Образцовое Окно вывода обновляется, чтобы включать эту модель, как показано в следующей фигуре.
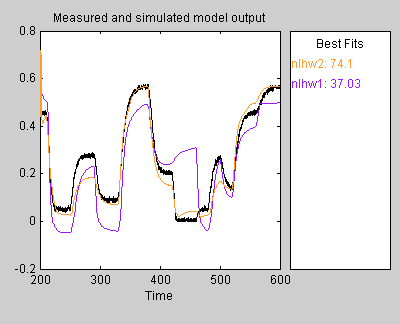
Область Best Fits Образцового Окна вывода показывает качество подгонки nlhw2.
В этом фрагменте примера вы изменяете значение по умолчанию структура модели Хаммерстайна-Винера путем изменения ее средства оценки нелинейности.
Если вы знаете, что ваша система включает насыщение или мертво-зональную нелинейность, можно задать эти специализированные средства оценки нелинейности в модели. Piecewise Linear и Sigmoid Network являются средствами оценки нелинейности для общего приближения нелинейности.
В диалоговом окне Nonlinear Models кликните по вкладке Configure.
Во вкладке I/O Nonlinearity, для входа Voltage, кликают по ячейке Nonlinearity и выбирают Sigmoid Network из списка. Кликните по соответствующей ячейке No. of Units и установите значение к 20.
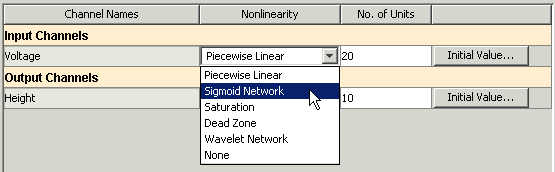
Нажмите Estimate.
Это действие добавляет модель nlhw3 в приложение System Identification. Это также обновляет Образцовое Окно вывода, как показано в следующей фигуре.
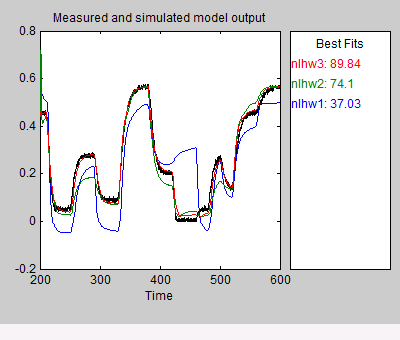
В диалоговом окне Nonlinear Models кликните по вкладке Configure.
Во вкладке I/O Nonlinearity, набор вход Voltage Nonlinearity к Wavelet Network. Это действие устанавливает No. of Units быть определенным автоматически по умолчанию.
Установите Height вывод Nonlinearity к One-dimensional Polynomial.
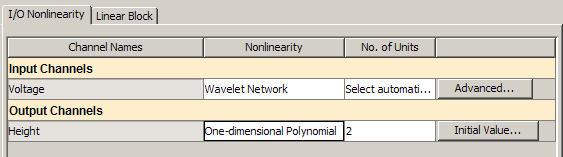
Нажмите Estimate.
Это действие добавляет модель nlhw4 в приложение System Identification. Это также обновляет Образцовое Окно вывода, как показано в следующей фигуре.
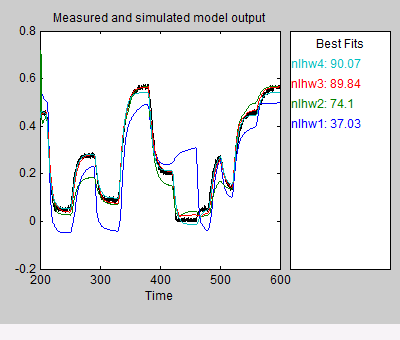
Лучшая модель является самой простой моделью, которая точно описывает динамику.
В этом примере лучшая образцовая подгонка была произведена в Изменении Средства оценки Нелинейности в Модели Хаммерстайна-Винера.