Моделирование черного ящика полезно, когда ваш главный интерес находится в подгонке данных независимо от конкретной математической структуры модели. Тулбокс обеспечивает несколько линейных и нелинейных структур модели черного ящика, которые традиционно были полезны для представления динамических систем. Эти образцовые структуры отличаются по сложности в зависимости от гибкости, необходимо объяснить динамику и шум в системе. Можно выбрать одну из этих структур и вычислить его параметры, чтобы соответствовать измеренным данным об ответе.
Моделирование черного ящика обычно является эмпирическим процессом, где вы оцениваете параметры различных структур и сравниваете результаты. Как правило, вы запускаете с простой линейной образцовой структуры и продвижения к более комплексным структурам. Вы можете также выбрать образцовую структуру, потому что вы более знакомы с этой структурой или потому что у вас есть определенные потребности приложения.
Самые простые линейные структуры черного ящика требуют, чтобы наименьшее количество опций сконфигурировало:
Передаточная функция, с данным количеством полюсов и нулей.
Линейная модель ARX, которая является самой простой моделью полинома ввода - вывода.
Модель в пространстве состояний, которую можно оценить путем определения количества образцовых состояний
Оценка некоторых из этих структур также использует неитеративные алгоритмы оценки, который далее уменьшает сложность.
Можно сконфигурировать образцовую структуру с помощью model order. Определение порядка модели отличается в зависимости от типа модели, которую вы выбираете. Например, если вы выбираете представление передаточной функции, порядок модели связан с количеством полюсов и нулей. Для представления пространства состояний порядок модели соответствует количеству состояний. В некоторых случаях, такой что касается линейного ARX и структур модели в пространстве состояний, можно оценить порядок модели от данных.
Если простые образцовые структуры не производят хорошие модели, можно выбрать структуры более сложной модели:
Определение более высокого порядка модели для той же линейной образцовой структуры. Более высокий порядок модели увеличивает образцовую гибкость для получения комплексных явлений. Однако излишне старшие разряды могут сделать модель менее надежной.
Явным образом моделирование шума:
y (t) =Gu (t) +He (t)
где модели H аддитивное воздействие путем обработки воздействия как вывода линейной системы, управляемой белым источником шума e (t).
Используя образцовую структуру, которая явным образом моделирует аддитивное воздействие, может помочь улучшить точность измеренного G компонента. Кроме того, такая образцовая структура полезна, когда ваш главный интерес использует модель для предсказания будущих значений ответа.
Используя различную линейную образцовую структуру.
Смотрите линейные образцовые структуры.
Используя нелинейную образцовую структуру.
Нелинейные модели имеют больше гибкости в получении комплексных явлений, чем линейные модели подобных порядков. Смотрите Нелинейные Образцовые Структуры.
В конечном счете вы выбираете самую простую образцовую структуру, которая обеспечивает лучшую подгонку к вашим результатам измерений. Для получения дополнительной информации смотрите Оценку Линейных Моделей Используя Быстрый запуск.
Независимо от структуры вы выбираете для оценки, можно упростить модель для потребностей приложения. Например, можно выделить измеренную динамику (G) от шумовой динамики (H), чтобы получить более простую модель, которая представляет только отношение между y и u. Можно также линеаризовать нелинейную модель о рабочей точке.
Линейная модель часто достаточна, чтобы точно описать системную динамику и, в большинстве случаев, необходимо сначала попытаться соответствовать линейным моделям. Если линейный образцовый вывод не соответственно воспроизводит измеренный вывод, вы можете должны быть использовать нелинейную модель.
Можно оценить потребность использовать нелинейную образцовую структуру путем графического вывода ответа системы к входу. Если вы замечаете, что ответы отличаются в зависимости от уровня на входе или вводят знак, попытайтесь использовать нелинейную модель. Например, если выходной ответ на вход подходит, быстрее, чем ответ на шаг вниз, вам может быть нужна нелинейная модель.
Прежде, чем создать нелинейную модель системы, которую вы знаете, нелинейно, попытайтесь преобразовать переменные ввода и вывода, таким образом, что отношение между преобразованными переменными линейно. Например, рассмотрите систему, которая имеет текущий и напряжение как входные параметры к спирали для нагрева воды и температура горячей жидкости как вывод. Вывод зависит от входных параметров через степень нагревателя, который равен продукту тока и напряжения. Вместо того, чтобы создать нелинейную модель для этого 2D входа и системы с одним выходом, можно создать новую входную переменную путем взятия продукта текущих и напряжения и затем создать линейную модель, которая описывает отношение между степенью и температурой.
Если вы не можете определить переменные преобразования, которые приводят к линейному соотношению между переменными ввода и вывода, можно использовать нелинейные структуры, такие как Нелинейный ARX или модели Хаммерстайна-Винера. Для списка поддерживаемых нелинейных образцовых структур и когда использовать их, смотрите Нелинейные Образцовые Структуры.
Можно использовать приложение System Identification или команды, чтобы оценить линейные и нелинейные модели различных структур. В большинстве случаев вы выбираете образцовую структуру и оцениваете параметры модели с помощью одной команды.
Рассмотрите систему массового пружинного демпфера, описанную приблизительно в Динамических системах и Моделях. Если вы не знаете уравнение движения этой системы, можно использовать подход моделирования черного ящика, чтобы создать модель. Например, можно оценить передаточные функции или модели в пространстве состояний путем определения порядков этих образцовых структур.
Передаточная функция является отношением полиномов:
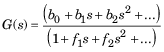
Для массово-пружинной системы демпфера эта передаточная функция:
![]()
который является системой без нулей и 2 полюсов.
В дискретное время передаточная функция системы массового пружинного демпфера может быть:
![]()
где порядки модели соответствуют количеству коэффициентов числителя и знаменателя (nb = 1 и nf = 2), и задержка ввода - вывода равняется экспоненте самой низкоуровневой z –1 в числителе (nk = 1).
В непрерывно-разовом можно создать линейную модель передаточной функции использование команды tfest:
m = tfest(data,2,0)
где data является вашими измеренными данными ввода - вывода, представленными как объект iddata, и порядок модели является набором количества полюсов (2) и количества нулей (0).
Точно так же можно создать структуру модели Output Error дискретного времени с помощью следующей команды:
m = oe(data,[1 2 1])
Порядок модели [nb nf nk] = [1 2 1]. Обычно, вы не знаете порядков модели заранее. Необходимо попробовать несколько стоимостей заказов модели, пока вы не находите порядки, которые производят приемлемую модель.
Также можно выбрать структуру пространства состояний, чтобы представлять систему массового пружинного демпфера и оценить параметры модели с помощью ssest или команды n4sid:
m = ssest(data,2)
где order = 2 представляет количество состояний в модели.
В моделировании черного ящика вам не нужно уравнение системы движения — только предположение порядков модели.
Для получения дополнительной информации о создавании моделей, смотрите Шаги для Использования Приложения System Identification и Образцовых Команд Оценки.