Оцените модель в пространстве состояний, использующую данные о частотном диапазоне или время
sys = ssest(data,nx)sys = ssest(data,nx,Name,Value)sys = ssest(___,opt)sys = ssest(data,init_sys)sys = ssest(data,init_sys,opt)[sys,x0] = ssest(___)sys = ssest(data,nx)sys, с помощью времени - или данные частотного диапазона, data. sys является моделью в пространстве состояний порядка nx и представляет:
A, B, C, D и K являются матрицами пространства состояний. u (t) является входом, y (t) является вывод, e (t) является воздействием, и x (t) является вектором состояний nx.
Все записи A, B, C и K являются свободными допускающими оценку параметрами по умолчанию. D фиксируется, чтобы обнулить по умолчанию, означая, что нет никакого сквозного соединения, за исключением статических систем (nx=0).
sys = ssest(data,nx,Name,Value)Name,Value. Используйте Form, аргументы пары "имя-значение" Feedthrough и DisturbanceModel, чтобы изменить поведение по умолчанию A, B, C, D и матриц K.
sys = ssest(___,opt)opt, который задает опции, такие как цель оценки, обработка начальных условий и числового метода поиска, используемого для оценки.
|
Идентифицированная модель в пространстве состояний, возвращенная как модель Информация о результатах оценки и используемых опциях хранится в свойстве
Для получения дополнительной информации об использовании | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Начальные состояния вычисляются во время оценки. Если Это значение также хранится в поле |
Получите измеренные данные ввода - вывода.
load icEngine.mat;
data = iddata(y,u,0.04);data является объектом iddata, содержащим 1 500 выборок данных ввода - вывода. Шаг расчета данных составляет 0,04 секунды.
Оцените модель в пространстве состояний для измеренных данных ввода - вывода. Определите оптимальный порядок модели в данной образцовой области значений порядка.
nx = 1:10; sys = ssest(data,nx);
Появляется график, который показывает сингулярные значения Ганкеля (SVD) для моделей порядков, заданных nx.
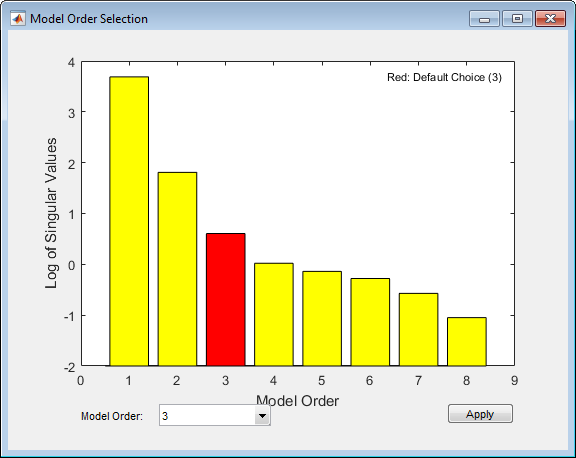
Состояния с относительно маленькими сингулярными значениями Ганкеля могут быть безопасно отброшены. Предложенным выбором порядка по умолчанию является 3.
Выберите порядок модели в Model Order выпадающий список и нажмите Apply.
Загрузите данные об отклике системы временного интервала.
load iddata7 z7;
Идентифицируйте модель в пространстве состояний четвертого порядка данных. Задайте известную задержку секунд 2 для первого входа и секунды 0 для второго входа.
nx = 4;
sys = ssest(z7(1:300),nx,'InputDelay',[2;0]);Получите упорядоченную 5-ю модель в пространстве состояний порядка для 2-й системы порядка от узкого сигнала пропускной способности.
Загрузите данные об оценке.
load regularizationExampleData eData;
Создайте модель передаточной функции, используемую для генерации данных об оценке (истинная система).
trueSys = idtf([0.02008 0.04017 0.02008],[1 -1.561 0.6414],1);
Оцените неупорядоченную модель в пространстве состояний.
opt = ssestOptions('SearchMethod','lm'); m = ssest(eData,5,'form','modal','DisturbanceModel','none','Ts',eData.Ts,opt);
Оцените упорядоченную модель в пространстве состояний.
opt.Regularization.Lambda = 10; mr = ssest(eData,5,'form','modal','DisturbanceModel','none','Ts',eData.Ts,opt);
Сравните образцовые выходные параметры с данными об оценке.
compare(eData,m,mr);

Сравните образцовые импульсные ответы.
impulse(trueSys,m,mr,50); legend('trueSys','m','mr');

Оцените модель в пространстве состояний измеренных данных ввода - вывода. Сконфигурируйте ограничения параметра и начальные значения для оценки с помощью модели в пространстве состояний.
Создайте модель idss, чтобы задать начальную параметризацию для оценки.
A = blkdiag([-0.1 0.4; -0.4 -0.1],[-1 5; -5 -1]); B = [1; zeros(3,1)]; C = [1 1 1 1]; D = 0; K = zeros(4,1); x0 = [0.1 0.1 0.1 0.1]; Ts = 0; init_sys = idss(A,B,C,D,K,x0,Ts);
Установка всех записей K к 0 создает модель idss без элемента воздействия состояния.
Используйте свойство Structure зафиксировать значения некоторых параметров модели. Сконфигурируйте модель так, чтобы B и K были зафиксированы, и только ненулевые записи A являются допускающими оценку.
init_sys.Structure.A.Free = (A~=0); init_sys.Structure.B.Free = false; init_sys.Structure.K.Free = false;
Записи в init_sys.Structure.A.Free определяют, свободны ли соответствующие записи в init_sys.A (true) или зафиксировали (false).
Загрузите результаты измерений и оцените модель в пространстве состояний с помощью ограничений параметра и начальных значений, заданных init_sys.
load iddata2 z2; sys = ssest(z2,init_sys);
Предполагаемые параметры sys удовлетворяют ограничения, заданные init_sys.
Считайте модель Simulink idF14Model. Линеаризация этой модели дает модель девятого порядка. Однако динамика модели может быть получена, не ставя под угрозу подходящее качество слишком много, с помощью модели более низкоуровневой.
Получите линеаризовавшую модель.
load_system('idF14Model'); io = getlinio('idF14Model'); sys_lin = linearize('idF14Model',io);
sys_lin является моделью в пространстве состояний девятого порядка с двумя выходными параметрами и одним входом.
Моделируйте переходной процесс линеаризовавшей модели и используйте данные, чтобы создать объект iddata.
Ts = 0.0444; t = (0:Ts:4.44)'; y = step(sys_lin,t); data = iddata([zeros(20,2);y],[zeros(20,1); ones(101,1)],Ts);
data является объектом iddata, который инкапсулирует переходной процесс sys_lin.
Сравните данные с линеаризацией модели.
compare(data,sys_lin);

Поскольку данные были получены путем симуляции линеаризовавшей модели, существует 100%-е соответствие между данными и образцовым ответом линеаризации.
Идентифицируйте модель в пространстве состояний с уменьшаемым порядком, который соответственно соответствует данным.
Определите оптимальный порядок модели.
nx = 1:9; sys1 = ssest(data,nx,'DisturbanceModel','none');
Появляется график, показывающий сингулярные значения Ганкеля (SVD) для моделей порядков, заданных nx.
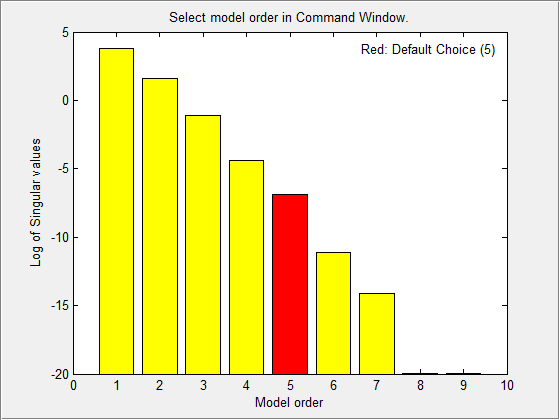
Состояния с относительно маленькими сингулярными значениями Ганкеля могут быть безопасно отброшены. График предлагает использовать модель пятого порядка.
В подсказке команды MATLAB выберите порядок модели для предполагаемой модели в пространстве состояний. Задайте порядок модели как 5 или нажмите Enter, чтобы использовать стоимость заказа по умолчанию.
Сравните данные с предполагаемой моделью.
compare(data,sys1);

sys1 обеспечивает 98,4%, подходящие для первого вывода и 97,7%, подходящие для второго вывода.
Исследуйте останавливающееся условие на алгоритм поиска.
sys1.Report.Termination.WhyStop
ans = 'Maximum number of iterations reached.'
Создайте набор опций оценки, который задает метод поиска 'lm' и позволяет максимум 50 поисковых итераций.
opt = ssestOptions('SearchMethod','lm'); opt.SearchOptions.MaxIterations = 50; opt.Display = 'on';
Идентифицируйте модель в пространстве состояний с помощью набора опции оценки и sys1 как модель инициализации оценки.
sys2 = ssest(data,sys1,opt);
Сравните ответ линеаризовавшего и предполагаемых моделей.
compare(data,sys_lin,sys2);

sys2 обеспечивает 99%, подходящих для первого вывода и 98%, подходящих для второго вывода при использовании 4 меньше состояний, чем sys_lin.
ssest инициализирует оценки параметра с помощью или неитеративного подхода подпространства или итеративного подхода оценки рациональной функции. Это затем совершенствовало значения параметров с помощью ошибочного подхода минимизации прогноза. Смотрите pem и ssestOptions для получения дополнительной информации.
[1] Ljung, L. System Identification: теория для пользователя, второго выпуска, верхнего Сэддл-Ривер, Нью-Джерси: Prentice Hall, 1999.
canon | iddata | idfrd | idgrey | idss | n4sid | pem | polyest | procest | ssestOptions | ssregest | tfest