В целом решатели возвращают локальный минимум. Результатом может быть глобальный минимум, но нет никакой гарантии, что это. В этом разделе описываются, почему решатели ведут себя этот путь, и дает предложения для способов искать глобальный минимум, в случае необходимости.
Минимум local функции является точкой, где значение функции меньше, чем в соседних точках, но возможно больше, чем в удаленной точке.
Минимум global является точкой, где значение функции меньше, чем во всех других допустимых точках.
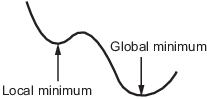
Обычно решатели Optimization Toolbox™ находят локальный оптимум. (Этот локальный оптимум может быть глобальным оптимумом.) Они находят оптимум в basin of attraction отправной точки. Для получения дополнительной информации о бассейнах привлекательности, смотрите Бассейны Привлекательности.
Существуют некоторые исключения к этому общему правилу.
Линейное программирование и положительные определенные проблемы квадратичного программирования выпуклы с выпуклыми выполнимыми областями, таким образом, существует только один бассейн привлекательности. Действительно, при определенном выборе опций, linprog игнорирует любую предоставленную пользователями отправную точку, и quadprog не требует один, хотя предоставляя можно иногда ускорять минимизацию.
Функции Global Optimization Toolbox, такие как simulannealbnd, пытаются искать больше чем один бассейн привлекательности.
Если вам нужен глобальный оптимум, необходимо найти начальное значение для решателя в бассейне привлекательности глобального оптимума.
Предложения для способов установить начальные значения, чтобы искать глобальный оптимум:
Используйте обычную сетку начальных точек.
Используйте случайные точки, чертившие от равномерного распределения, если ваша проблема имеет все свои ограниченные координаты. Используйте точки, чертившие от нормальных, экспоненциальных, или других случайных распределений, если некоторые компоненты неограниченны. Чем меньше вы знаете о местоположении глобального оптимума, тем более распространено ваше случайное распределение должно быть. Например, нормальные распределения редко выборка больше чем три стандартных отклонения далеко от их средних значений, но распределения Коши (плотность 1 / (π (1 + x 2))) делает чрезвычайно разрозненные выборки.
Используйте идентичные начальные точки с добавленными случайными возмущениями на каждой координате, ограниченный, нормальный, экспоненциальный, или другом.
Если у вас есть лицензия Global Optimization Toolbox, используйте решатели MultiStart или GlobalSearch. Эти решатели автоматически генерируют случайные стартовые точки в границах.
Чем больше вы знаете о возможных начальных точках, тем более фокусируется и успешен ваш поиск будет.
Если целевая функция, f (x) сглажен, вектор – ∇f (x) точки в направлении, где f (x) уменьшается наиболее быстро. Уравнение быстрейшего спуска, а именно,
приводит к пути x (t), который переходит к локальному минимуму, когда t становится большим. Обычно x начальных значений (0), которые являются друг близко к другу, дает пути к быстрейшему спуску, которые склоняются к той же минимальной точке. basin of attraction для быстрейшего спуска является набором начальных значений, которые приводят к тому же локальному минимуму.
Следующие данные показывают два одномерных минимума. Данные показывают различные бассейны привлекательности с различными стилями линии и показывают направления быстрейшего спуска со стрелками. Для этого и последующих фигур, черные точки представляют локальные минимумы. Каждый путь к быстрейшему спуску, запускающийся в точке x (0), переходит к черной точке в бассейне, содержащем x (0).
Одномерные бассейны
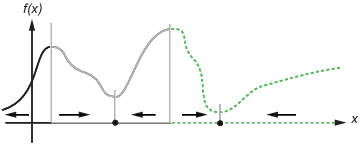
Следующие данные показывают, как пути к быстрейшему спуску могут быть более сложными в большем количестве размерностей.
Один бассейн привлекательности, показывая пути к быстрейшему спуску от различных отправных точек
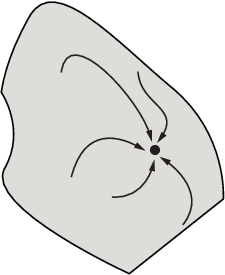
Следующие данные показывают еще более сложные пути и бассейны привлекательности.
Несколько бассейнов привлекательности

Ограничения могут разбить один бассейн привлекательности в несколько частей. Например, считайте минимизацию y подвергающийся:
y ≥ |x |
y ≥ 5 – 4 (x –2) 2.
Данные показывают два бассейна привлекательности с конечными пунктами.
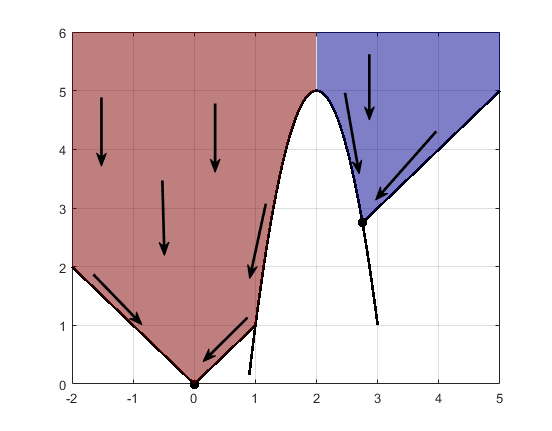
Пути к быстрейшему спуску являются прямыми линиями вниз к ограничительным контурам. От ограничительных контуров пути к быстрейшему спуску перемещаются вниз вдоль контуров. Конечный пункт или (0,0) или (11/4,11/4), в зависимости от того, является ли начальный x - значение выше или ниже 2.