Определите системную жесткость

Определение числовой жесткости вашей модели помогает вам решить между использованием неявного или явного решателя фиксированного шага для симуляции в реальном времени. Чтобы определить числовую жесткость, сначала используйте рабочий процесс подготовки к модели реального времени, чтобы оптимизировать скорость и точность вашей модели. Затем моделируйте свою модель с помощью и явных и неявных решателей фиксированного шага. Сравните результаты симуляции, чтобы видеть, как решатели ведут себя. Если ваша модель численно жестка, явный решатель обычно показывает маленькие колебания вокруг требуемого решения.

Неявные решатели более устойчивы, чем явные решатели, однако, явные решатели быстрее. Для устойчивых результатов при выполнении симуляции в реальном времени с численно жесткой моделью используйте неявный решатель фиксированного шага. Если ваша модель не жестка, используйте явный решатель, чтобы максимизировать скорость симуляции.

В этом примере вы получаете ссылочные результаты путем симуляции пневматической модели с решателем переменного шага. Вы также конфигурируете и моделируете модель с помощью неявного и затем явной глобальной переменной фиксированного шага решатель Simulink^®. Затем вы сравниваете результаты всех трех симуляций, чтобы определить, жестка ли пневматическая модель численно.

Получите ссылочные результаты

Открыть модель, в командной строке MATLAB^®, введите:
```
ssc_pneumatic_rts_reference
```
Сохраните модель как stiffness_model к перезаписываемой папке на пути MATLAB.
Моделируйте модель.
Присвойте результаты симуляции новым переменным.
```
yRef = yout;
tRef = tout;
```

Постройте результаты симуляции переменного шага.

h1 = figure;
plot(tRef,yRef)
h1Leg = legend({'Reference'});
title('Speed')
xlabel('Time (s)')
ylabel('Speed (rpm)')

Моделируйте с неявным решателем Фиксированного Шага

Сконфигурируйте модель для симуляции фиксированного шага с неявным решателем ode14x. В панели Решателя параметров конфигурации, наборе:
- Type к Fixed-step
- Solver к ode14x (extrapolation)
- Под Additional options, Fixed-step size (fundamental sample time) к 1e-3
- Number of Newton's iterations к 1.
Нажмите Apply.
Моделируйте модель.
Присвойте результаты симуляции новым переменным.
```
yOde14x = yout;
tOde14x = tout;
```
Используйте функцию stairs, чтобы построить результаты неявной симуляции фиксированного шага, таким образом, вы видите, как решатель ведет себя, когда это выполняет каждый шаг в симуляции.
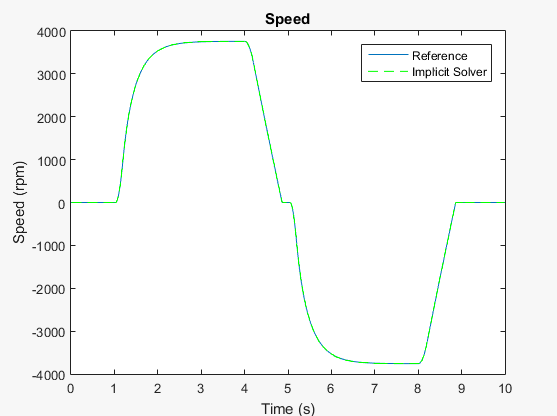
```
h1
hold on
stairs(tOde14x,yOde14x,'g--')
h1Leg = legend({'Reference','Implicit Solver'});
```
Результаты появляются то же самое.

Моделируйте с явным решателем Фиксированного Шага

Сконфигурируйте модель для симуляции фиксированного шага с явным решателем фиксированного шага ode5. В панели Решателя параметров конфигурации, наборе:
- Type к Fixed-step
- Solver к ode5 (Dormand-Prince)
Нажмите OK.
Отфильтруйте входной сигнал, чтобы обеспечить необходимую входную производную для явного решателя. В диалоговом окне блока PS-S Simulink Converter, на вкладке Input Handling, устанавливает Filtering and derivatives на Filter Input. Нажмите OK.
Моделируйте модель.
Присвойте результаты симуляции новым переменным.
```
yOde5 = yout;
tOde5 = tout;
```
Используйте функцию stairs, чтобы построить результаты явной симуляции фиксированного шага.
```
h1
hold on
stairs(tOde5,yOde5,'r-')
h1Leg = legend({'Reference','Implicit Solver','Explicit Solver'});
```
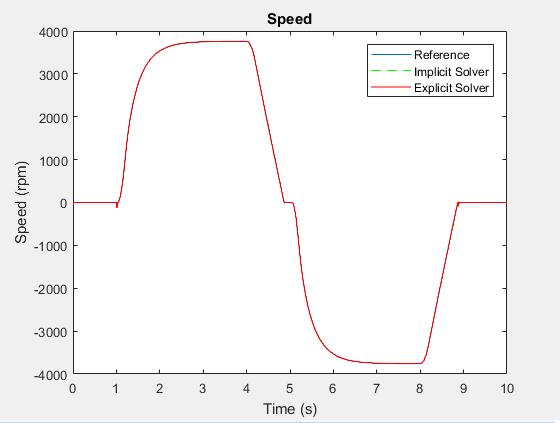
Результаты отличаются в точках перегиба.

Анализ результатов

Чтобы видеть результаты более тесно, масштабируйте к точке перегиба сразу после времени t = ~ 1 секунда.

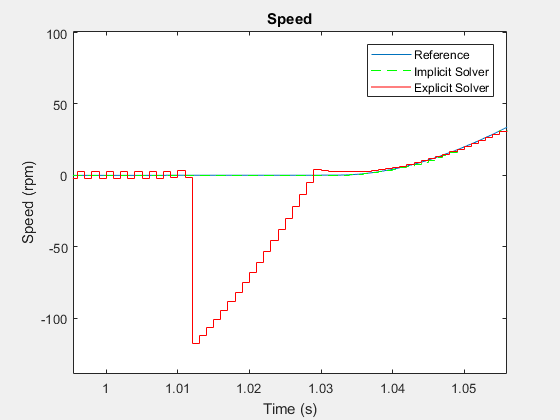
Неявный решатель следует за путем, который подобен пути, который решатель переменного шага берет при генерации ссылочных результатов. Колебания, что явные выставки решателя указывают, что модель численно жестка. Колебания также указывают, что явный решатель является более в вычислительном отношении дорогостоящим, чем неявный решатель для симуляции жесткой модели. Используйте глобальную переменную или локальный неявный решатель фиксированного шага для симуляции в реальном времени с численно жесткими моделями, чтобы избежать ненужной вычислительной стоимости.

Смотрите также

stairs

Документация