mixsyn

H _∞ метод синтеза смешанной чувствительности для устойчивого управления loopshaping проект

Синтаксис

[K,CL,GAM,INFO] = mixsyn(G,W1,W2,W3)
[K,CL,GAM,INFO] = mixsyn(G,W1,W2,W3,KEY1,VALUE1,KEY2,VALUE2,...)

Описание

[K,CL,GAM,INFO]=mixsyn(G,W1,W2,W3) вычисляет контроллер K, который минимизирует H _∞ норма передаточной функции с обратной связью взвешенная смешанная чувствительность

$T_{y 1 u 1} ≜ [\begin{matrix} W_{1} S \\ W_{2} R \\ W_{3} T \end{matrix}]$

где S и T называются sensitivity и complementary sensitivity, соответственно. R измеряет усилие по управлению, передаточную функцию от ссылочного входа до входа объекта. S, R и T дают

$\begin{matrix} S = (^{I + G K) - 1} \\ R = K (^{I + G K) - 1} \\ T = G K (^{I + G K) - 1} \end{matrix}$

Следующие данные показывают соответствующую архитектуру управления.

Передаточная функция с обратной связью _Ty1u1 для смешанной чувствительности mixsyn.

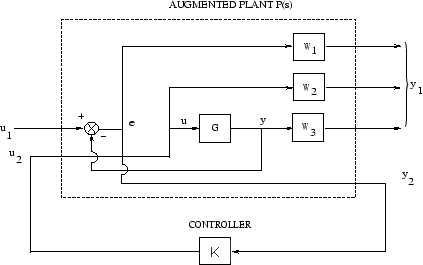
Возвращенный K контроллера таков, что S, R и T удовлетворяют следующие формирующие цикл неравенства:

$\begin{array}{l} \bar{σ} (S (j ω)) \leq γ \underline{σ} (W_{1}^{- 1} (j ω)) \\ \bar{σ} (R (j ω)) \leq γ \underline{σ} (W_{2}^{- 1} (j ω)) \\ \bar{σ} (T (j ω)) \leq γ \underline{σ} (W_{3}^{- 1} (j ω)) \end{array}$

где γ = GAM. Таким образом инверсии W ₁ и W ₃ определяют формы чувствительности S и дополнительная чувствительность T. Как правило, вы выбираете W₁, который является большим в желаемой пропускной способности управления, чтобы достигнуть хорошего затухания воздействия (т.е. производительность). Точно так же вы обычно выбираете W₃, который является большим вне пропускной способности управления, которая помогает гарантировать хороший запас устойчивости (т.е. робастность).

Для размерной совместимости каждого из этих трех весов W ₁, W ₂ и W ₃ должен быть или пустым, скалярным (SISO) или иметь соответствующие входные размерности _NY, _NU и _NY, где G является _NY-by-_NU. Если один из весов не нужен, можно просто присвоить пустую матрицу []; например, P = AUGW(G,W1,[],W3) является SYS, но без второй строки (без строки, содержащей W2).

Примеры

свернуть все

Формирование цикла с mixsyn

Скрипт Open Live Script

Этот пример показывает использование mixsyn для чувствительности и дополнительного формирования цикла чувствительности.

Создайте модель объекта управления и функции взвешивания.

s = zpk('s');
G = (s-1)/(s+1)^2;
W1 = 10*(0.1*s+1)/(100*s+1);
W2 = 0.1*(0.1*s+1)/(0.01*s+1);
W3 = 0.01*(10*s+1)/(0.01*s+1);

[K,CL,GAM] = mixsyn(G,W1,W2,W3);

mixsyn формирует сингулярные значения функции чувствительности S, дополнительная функция чувствительности T и усилие по управлению R = K*S. Исследуйте результаты синтеза и формы этих передаточных функций.

S = feedback(1,G*K);
R = K*S;
T = 1-S;
sigma(S,'b',R,'r',T,'g',GAM/W1,'b-.',ss(GAM/W2),'r-.',GAM/W3,'g-.',{1e-3,1e3})
legend('S','R','T','GAM/W1','GAM/W2','GAM/W3','Location','SouthWest')
grid

Ограничения

Передаточные функции G, W ₁, W ₂ и W ₃ должны быть соответствующими, т.е. ограниченные как s → ∞ или, в случае дискретного времени, как z → ∞. Кроме того, W ₁, W ₂ и W ₃ должен быть стабильным. Объект G должен быть stabilizable и обнаруживаемым; еще, P не будет stabilizable никаким K.

Алгоритмы

[K,CL,GAM,INFO] = mixsyn(G,W1,W2,W3,KEY1,VALUE1,KEY2,VALUE2,...)

эквивалентно

[K,CL,GAM,INFO] = hinfsyn(augw(G,W1,W2,W3),KEY1,VALUE1,KEY2,VALUE2,...)

mixsyn принимает весь одинаковый пары значения ключа как hinfsyn.

Смотрите также

augw | hinfsyn

Документация