Вычислите L 2 нормы непрерывно-разовой системы в обратной связи с системой дискретного времени
[gaml,gamu] = sdhinfnorm(sdsys,k) [gaml,gamu] = sdhinfnorm(sdsys,k,delay) [gaml,gamu] = sdhinfnorm(sdsys,k,delay,tol)
[gaml,gamu] = sdhinfnorm(sdsys,k) вычисляет L, который содержат 2 вызванных нормы непрерывно-разового объекта LTI, sdsys, в обратной связи с контроллером дискретного времени, k, соединенным через идеальный сэмплер и нулевой порядок (см. фигуру ниже). sdsys должен быть строго соответствующим, таким, что постоянное усиление обратной связи должно быть нулем. Выходные параметры, gamu и gaml, являются верхними и нижними границами на вызванном L 2 нормы выборочных данных система с обратной связью.
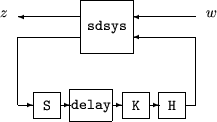
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay) включает входной параметр delay. delay является неотрицательным целым числом, сопоставленным с количеством вычислительных задержек контроллера. Значение по умолчанию задержки 0.
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay,tol) включает входной параметр, tol, который задает различие между верхними и нижними границами, когда поиск останавливается. Значение по умолчанию tol 0.001.
Рассмотрите разомкнутый цикл, непрерывно-разовая передаточная функция p = 30/s(s+30) и непрерывно-разовый controller k = 4/(s+4). Непрерывно-разовая система с обратной связью имеет пиковое значение через частоту 1.
p = ss(tf(30,[1 30])*tf([1],[1 0]));
k = ss(tf(4,[1 4]));
cl = feedback(p,k);
norm(cl,'inf')
ans =
1
Первоначально контроллер должен быть реализован на уровне частоты дискретизации 1,5 Гц. Норма выборочных данных системы с обратной связью с контроллером дискретного времени 1.0.
kd = c2d(k,0.75,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
3.7908 3.7929
Из-за значительных различий в норме между непрерывно-разовыми и выборочными данными система с обратной связью частота дискретизации контроллера увеличена с 1,5 Гц до 5 Гц. Норма выборочных данных новой системы с обратной связью 3.79.
kd = c2d(k,0.2,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
1.0044 1.0049
sdhinfnorm использует изменения формул, описанных в статье Бэмиха и Пирсона, чтобы получить эквивалентную систему дискретного времени. (Эти изменения сделаны, чтобы улучшить числовое создание условий алгоритмов.) Предварительный шаг должен определить, является ли норма непрерывно-разовой системы за один период выборки свободно меньше, чем данное значение. Это требует поиска и является, в вычислительном отношении, относительно дорогим шагом.
Bamieh, степень бакалавра гуманитарных наук и Дж.Б. Пирсон, “Общие рамки для Линейных Периодических Систем с Приложениями к Управлению Выборочных данных”, Транзакции IEEE на Автоматическом управлении, издании AC-37, 1992, стр 418-435.