Exponenta Banner

stft

Кратковременное преобразование Фурье

свернуть все на странице

Синтаксис

s = stft(x)
s = stft(x,fs)
s = stft(x,ts)
s = stft(___,Name,Value)
[s,f] = stft(___)
[s,f,t] = stft(___)
stft(___)

Описание

s = stft(x) возвращает кратковременное преобразование Фурье (STFT) x.

пример

s = stft(x,fs) возвращает STFT x с помощью частоты дискретизации fs.

s = stft(x,ts) возвращает STFT x с помощью шага расчета ts.

пример

s = stft(___,Name,Value) задает аргументы пары "имя-значение" использования дополнительных опций. Опции включают окно FFT и длину. Эти аргументы могут быть добавлены к любому из предыдущих входных синтаксисов.

[s,f] = stft(___) возвращает частоты f, в котором оценен STFT.

[s,f,t] = stft(___) возвращает времена, в которые оценен STFT.

stft(___) без выходных аргументов строит значение STFT в окне текущей фигуры. STFT построен как двухсторонний и в центре.

Примеры

свернуть все

Скрипт Open Live Script

Сгенерируйте две секунды управляемого осциллятора напряжения вывод, которым управляет синусоида, выбранная на уровне 10 кГц.

fs = 10e3;
t = 0:1/fs:2;
x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);

Вычислите и постройте STFT сигнала. Используйте окно Kaiser длины 256 и сформируйте параметр β=5. Задайте длину перекрытия как 220 выборок и длина ДПФ как 512 точек. Постройте STFT с палитрой по умолчанию и представлением.

stft(x,fs,'Window',kaiser(256,5),'OverlapLength',220,'FFTLength',512);

Измените представление, чтобы отобразить STFT как график водопада. Установите палитру на jet.

view(-45,65)
colormap jet

Скрипт Open Live Script

Сгенерируйте квадратичный щебет, выбранный на уровне 1 кГц в течение 2 секунд. Мгновенная частота составляет 100 Гц в t=0 и кресты 200 Гц в t=1 второй.

ts = 0:1/1e3:2;

f0 = 100;
f1 = 200;

x = chirp(ts,f0,1,f1,'quadratic',[],'concave');

Вычислите и отобразите STFT квадратичного щебета с длительностью 1 мс.

d = seconds(1e-3);
win = hamming(100,'periodic');

stft(x,d,'Window',win,'OverlapLength',98,'FFTLength',128);

Входные параметры

свернуть все

Входной сигнал, заданный как вектор или MATLAB® timetable.

Примечание

Если вы инвертируете s с помощью istft и хотите результат быть той же длиной как x, значение (length(x)-noverlap)/(length(window) - noverlap) должно быть целым числом.

Пример: x = chirp(0:1/4e3:2,250,1,500,'quadratic')

Типы данных: double | single
Поддержка комплексного числа: Да

Частота дискретизации, заданная как положительная скалярная величина. Этот аргумент применяется только, когда x является вектором.

Типы данных: double | single

Шаг расчета, заданный как скаляр duration. Этот аргумент применяется только, когда x является вектором.

Пример: seconds(1) является скаляром duration представление различия с 1 вторым разом между последовательными выборками сигнала.

Типы данных: double | single

Аргументы в виде пар имя-значение

Укажите необязательные аргументы в виде пар ""имя, значение"", разделенных запятыми. Имя (Name) — это имя аргумента, а значение (Value) — соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: окна stft('Window',win,'OverlapLength',50,'FFTLength',128) данные с помощью окна win, с 50 выборками накладываются между смежными сегментами и 128 БПФ точки.

Спектральное окно, заданное как пара, разделенная запятой, состоящая из 'Window' и вектора. Если вы не задаете окно или задаете его как пустой, функция использует окно Hann длины 128. Длина Window должна быть больше, чем или равной 2.

Для списка доступных окон смотрите Windows.

Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Hann длины N + 1.

Типы данных: double | single

Количество перекрытых выборок, заданных как неотрицательное целое число, меньшее, чем длина window. Если вы не используете 'OverlapLength' или задаете его как пустой, это установлено в самое большое целое число меньше чем 75% длины окна, которая является 96 выборками для окна Hann по умолчанию.

Типы данных: double | single

Количество точек ДПФ, заданных как положительное целое число. Значение должно быть больше, чем или равным длине окна. Если длина входного сигнала является меньше, чем длина ДПФ, данные дополнены нулями.

Типы данных: double | single

Частотный диапазон, заданный как true или false. Если эта опция установлена в true, то спектр сосредоточен и вычисляется на интервале –π к π. В противном случае спектр вычисляется на интервале 0 к 2π.

Выходные аргументы

свернуть все

Кратковременное преобразование Фурье, возвращенное как вектор. Увеличения времени через столбцы s и частоты увеличивают вниз строки.

  • Если x сигнала имеет длину Nx, то s имеет столбцы k, где k = ⌊ (Nx – L) / (length(window) – L) ⌋, где window является вектором, L, равен 'OverlapLength', и ⌊ ⌋ символы обозначают функцию пола.

  • Количество строк в s равно значению, заданному в 'FFTLength'.

Типы данных: double | single

Частоты, на которых оценен STFT, возвратились как вектор.

Типы данных: double | single

Моменты времени, возвращенные как вектор. t содержит временные стоимости, соответствующие центрам сегментов данных, используемых, чтобы вычислить кратковременные оценки спектра мощности.

  • Если частота дискретизации, которую обеспечивается fs, то вектор содержит временные стоимости в секундах.

  • Если шаг расчета, который обеспечивается ts, то вектор является массивом длительности с тем же форматом времени как вход.

  • Если никакая информация времени не предоставляется, то вектор содержит демонстрационные числа.

Типы данных: double | single

Алгоритмы

Кратковременное преобразование Фурье (STFT) используется, чтобы анализировать, как содержимое частоты неустановившегося сигнала изменяется в зависимости от времени.

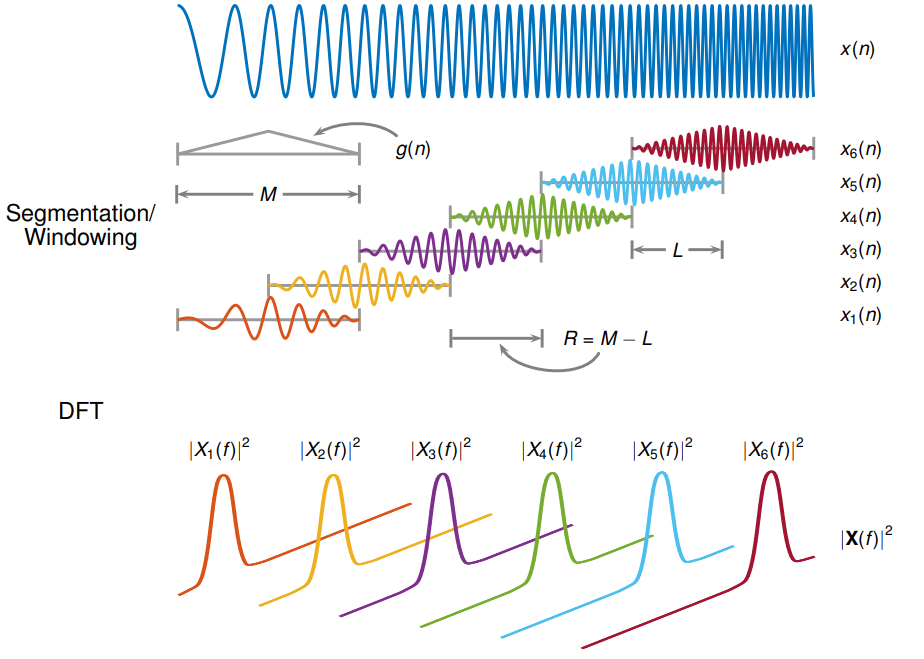
STFT сигнала вычисляется путем скольжения analysis window длины M по сигналу и вычислению дискретного преобразования Фурье оконных данных. Окно скачкообразно двигается по исходному сигналу с промежутками в R выборки. Функции окна Most сужаются в ребрах, чтобы избежать спектрального вызова. Если ненулевая длина перекрытия L задан, добавление перекрытия, которое оконные сегменты компенсируют затухание сигнала в ребрах окна. ДПФ каждого оконного сегмента добавляется к матрице, которая содержит значение и фазу для каждого момента времени и частоты. Количество строк в матрице STFT равняется количеству точек ДПФ, и количеством столбцов дают

k=⌊Nx−LM−L⌋,

где Nx длина исходного сигнала x(n) и ⌊⌋ символы обозначают функцию пола.

Матрицей STFT дают X(f)=[X1(f)X2(f)X3(f)⋯Xk(f)] таким образом, что mэлемент th этой матрицы

Xm(f)=∑n=−∞∞x(n)g(n−mR)e−j2πfn,

где

  • g(n) — Функция окна длины M.

  • Xm(f) — ДПФ оконных данных сосредоточен во время mR.

  • R — Скачкообразно переместите размер между последовательными ДПФ, размер транзитного участка является различием между длиной окна Mи длина перекрытия L.

Значение, в квадрате из STFT, приводит к представлению spectrogram степени спектральная плотность функции.

Ссылки

[1] Mitra, цифровая обработка сигналов Сэнджита К.: компьютерный подход. 2-й Эд. Нью-Йорк: McGraw-Hill, 2001.

[2] Смит, Обработка Звукового сигнала Дж. О. Спектрэла. https://ccrma.stanford.edu/~jos/sasp/, онлайновая книга, 2 011 выпусков, получил доступ к ноябрю 2018.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Функции

Введенный в R2019a

Документация Signal Processing Toolbox
Поддержка