Документация

Почему Windows использования?

И в создании цифровых фильтров и в спектральной оценке, выбор функции работы с окнами может играть важную роль в определении качества полных результатов. Основная роль окна должна ослабить эффекты Явления Гиббса, которое следует из усечения бесконечного ряда.

Доступные функции окна

Инструменты графического интерфейса пользователя

Два инструмента графического интерфейса пользователя обеспечиваются для работы с окнами в продукте Signal Processing Toolbox™:

Обратитесь к страницам с описанием для получения дальнейшей информации.

Основные формы

Основное окно является прямоугольным окном, вектором из единиц соответствующей длины. Прямоугольное окно длины 50

n = 50;
w = rectwin(n);

Этот тулбокс хранит окна в вектор-столбцах условно, таким образом, эквивалентное выражение

w = ones(50,1);

Чтобы использовать приложение Window Designer, чтобы создать это окно, ввести

windowDesigner

Приложение открывается Окном Хэмминга по умолчанию. Чтобы визуализировать прямоугольное окно, установите   Type = Rectangular и   Length = 50 в панели информации об Активном окне и затем нажмите Apply.

Бартлетт (или треугольный) окно является сверткой двух прямоугольных окон. Функции bartlett и triang вычисляют подобные треугольные окна с тремя важными различиями. Функция bartlett всегда возвращает окно с двумя нулями на концах последовательности, так, чтобы для нечетного n, центральная секция bartlett(n+2) была эквивалентна triang(n):

Bartlett = bartlett(7);
isequal(Bartlett(2:end-1),triang(5))

ans =
     1

Для n даже, bartlett является все еще сверткой двух прямоугольных последовательностей. Нет никакого стандартного определения для треугольного окна для n даже; наклоны линейных сегментов результата triang немного более круты, чем те из bartlett в этом случае:

w = bartlett(8); 
[w(2:7) triang(6)]

Вы видите различие между четными и нечетными окнами Бартлетта в Window Designer.

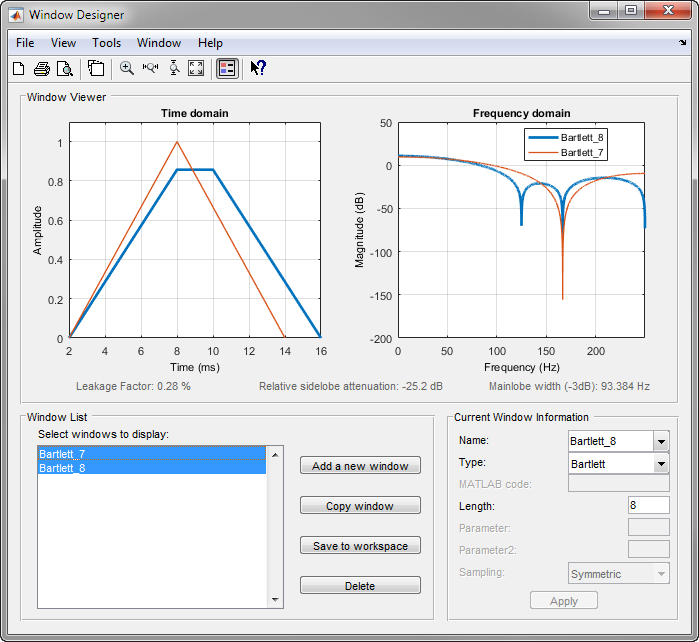
Итоговое различие между Бартлеттом и треугольными окнами очевидно в преобразованиях Фурье этих функций. Преобразование Фурье окна Бартлетта отрицательно для n даже. Преобразование Фурье треугольного окна, однако, является всегда неотрицательным.

Следующая фигура, которая строит нулевые фазовые отклики окон Бартлетта и Triangular с 8 точками, иллюстрирует различие.

zerophase(bartlett(8))
hold on
zerophase(triang(8))
legend('Bartlett','Triangular')
axis([0.3 1 -0.2 0.5])

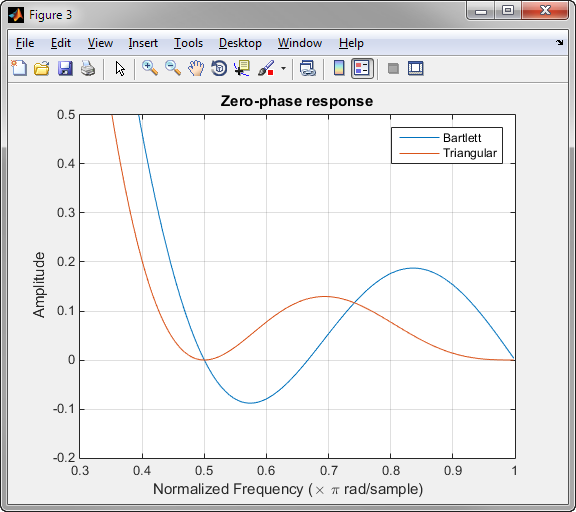
Это различие может быть важным при выборе окна для некоторых спектральных методов оценки, таких как метод Blackman-Tukey. Blackman-Tukey составляет спектральное мнение путем вычисления преобразования Фурье последовательности автокорреляции. Получившаяся оценка может быть отрицательной на некоторых частотах, если преобразование Фурье окна отрицательно.