Точный алгоритм линеаризации

Программное обеспечение Simulink^® Control Design™ линеаризует модели с помощью подхода блока блоком. Программное обеспечение индивидуально линеаризует каждый блок в вашей модели Simulink и производит линеаризацию полной системы путем объединения отдельной линеаризации блока.

Программное обеспечение определяет уровни на входе и государственные уровни для каждого блока от рабочей точки, и запрашивает якобиан для этих уровней от каждого блока.

Для некоторых блоков программное обеспечение не может вычислить аналитическую линеаризацию. Например:

Некоторая нелинейность не имеет заданного якобиана.
Некоторые дискретные блоки, такие как диаграммы состояний и инициированные подсистемы, имеют тенденцию линеаризовать, чтобы обнулить.
Некоторые блоки не реализуют якобиан.
Авторские блоки, такие как Блоки s-function и блоки MATLAB function, не имеют аналитических Якобианов.

Можно задать пользовательскую линеаризацию для любых таких блоков, для которых вы знаете ожидаемую линеаризацию. Если вы не задаете пользовательскую линеаризацию, программное обеспечение находит линеаризацию путем беспокойства входных параметров блока и состояний и измерения ответа на эти возмущения. Для получения дополнительной информации смотрите Возмущение Отдельных Блоков.

Непрерывно-разовые модели

Программное обеспечение Simulink Control Design позволяет вам линеаризовать непрерывно-разовые нелинейные системы. Получившаяся линеаризовавшая модель находится в форме пространства состояний.

В непрерывное время уравнения пространства состояний нелинейной системы:

$\begin{array}{l} \dot{x} (t) = f (x (t), u (t), t) \\ y (t) = g (x (t), u (t), t) \end{array}$

где x (t) являются системными состояниями, u (t) являются входными сигналами, и y (t) являются выходными сигналами.

Чтобы описать линеаризовавшую модель, задайте новый набор переменных состояний, входных параметров и выходных параметров, сосредоточенных о рабочей точке:

$\begin{array}{l} δ x (t) = x (t) - x_{0} \\ δ u (t) = u (t) - u_{0} \\ δ y (t) = y (t) - y_{0} \end{array}$

Вывод системы в рабочей точке является y (t0) =g (x0, u0, t0) =y0.

Линеаризовавшие уравнения пространства состояний с точки зрения δx (t), δu (t), и δy (t):

$\begin{array}{l} δ \dot{x} (t) = A δ x (t) + B δ u (t) \\ δ y (t) = C δ x (t) + D δ u (t) \end{array}$

где A, B, C, и D являются постоянными содействующими матрицами. Этими матрицами являются Якобианы системы, оцененной в рабочей точке:

$\begin{array}{l} A = {\frac{\partial f}{\partial x} |}_{t_{0}, x_{0}, u_{0}} B = {\frac{\partial f}{\partial u} |}_{t_{0}, x_{0}, u_{0}} \\ C = {\frac{\partial g}{\partial x} |}_{t_{0}, x_{0}, u_{0}} D = {\frac{\partial g}{\partial u} |}_{t_{0}, x_{0}, u_{0}} \end{array}$

Это линейное независимое от времени приближение к нелинейной системе допустимо в области вокруг рабочей точки в t=t0, x (t0) =x0, и u (t0) =u0. Другими словами, если значения системных состояний, x (t), и входные параметры, u (t), достаточно близки к рабочей точке, система ведет себя приблизительно линейно.

Передаточная функция линеаризовавшей модели является отношением Преобразования Лапласа δy (t) и Преобразования Лапласа δu (t):

$P_{l i n} (s) = \frac{δ Y (s)}{δ U (s)}$

Многоскоростные модели

Программное обеспечение Simulink Control Design позволяет вам линеаризовать многоскоростные нелинейные системы. Получившаяся линеаризовавшая модель находится в форме пространства состояний.

Многоскоростные модели включают состояния с различными уровнями выборки. В многоскоростных моделях переменные состояния изменяют значения в разное время и с различными частотами. Некоторые переменные могут изменяться постоянно.

Общие уравнения пространства состояний нелинейной, многоскоростной системы:

$\begin{matrix} \dot{x} (t) & = & f (x (t), x_{1} (k_{1}), \dots, x_{m} (k_{m}), u (t), t) \\ x_{1} (k_{1} + 1) & = & f_{1} (x (t), x_{1} (k_{1}), \dots, x_{m} (k_{m}), u (t), t) \\ ⋮ & ⋮ \\ x_{m} (k_{m} + 1) & = & f_{i} (x (t), x_{1} (k_{1}), \dots, x_{m} (k_{m}), u (t), t) \\ y (t) & = & g (x (t), x_{1} (k_{1}), \dots, x_{m} (k_{m}), u (t), t) \end{matrix}$

где k1..., км являются целочисленными значениями и $t_{k_{1}}$ ,..., $t_{k_{m}}$ дискретные времена.

Линеаризовавшие уравнения, которые аппроксимируют эту нелинейную систему как односкоростную дискретную модель:

$\begin{matrix} δ x_{k + 1} & \approx & A δ x_{k} + B δ u_{k} \\ δ y_{k} & \approx & C δ x_{k} + D δ u_{k} \end{matrix}$

Уровень линеаризовавшей модели обычно является наименьшим общим кратным шагов расчета, которое обычно является самым медленным шагом расчета.

Для получения дополнительной информации смотрите Линеаризацию Многоскоростных моделей.

Возмущение отдельных блоков

Программное обеспечение Simulink Control Design линеаризует блоки, которые не имеют предварительно запрограммированной линеаризации с помощью числового возмущения. Программное обеспечение вычисляет линеаризацию блока путем числового беспокойства состояний и входных параметров блока о рабочей точке блока.

Алгоритм возмущения блока вводит небольшое возмущение нелинейному блоку и измеряет ответ на это возмущение. Различие по умолчанию между встревоженным значением и значением рабочей точки $10^{- 5} (1 + | x |)$ , где x является значением рабочей точки. Программное обеспечение использует это возмущение и получившийся ответ, чтобы вычислить линейное пространство состояний этого блока. Для получения информации о том, как изменить уровни возмущения для отдельных блоков, смотрите Уровень Возмущения Изменения Блоков, Встревоженных Во время Линеаризации.

В целом непрерывно-разовым нелинейным блоком Simulink в форме пространства состояний дают:

$\begin{array}{l} \dot{x} (t) = f (x (t), u (t), t) \\ y (t) = g (x (t), u (t), t) . \end{array}$

В этих уравнениях x (t) представляет состояния блока, u (t) представляет входные параметры блока, и y (t) представляет выходные параметры блока.

Линеаризовавшая модель этой системы допустима в небольшой области вокруг рабочей точки t=t0, x (t0) =x0, u (t0) =u0, и y (t0) =g (x0, u0, t0) =y0.

Чтобы описать линеаризовавший блок, задайте новый набор переменных состояний, входных параметров и выходных параметров, сосредоточенных о рабочей точке:

$\begin{array}{l} δ x (t) = x (t) - x_{0} \\ δ u (t) = u (t) - u_{0} \\ δ y (t) = y (t) - y_{0} \end{array}$

Линеаризовавшие уравнения пространства состояний с точки зрения этих новых переменных:

$\begin{array}{l} δ \dot{x} (t) = A δ x (t) + B δ u (t) \\ δ y (t) = C δ x (t) + D δ u (t) \end{array}$

Линейное независимое от времени приближение к нелинейной системе допустимо в области вокруг рабочей точки.

Матрицы пространства состояний A, B, C, и D этой линеаризовавшей модели представляют Якобианы блока.

Чтобы вычислить матрицы пространства состояний во время линеаризации, программное обеспечение выполняет эти операции:

Тревожит состояния и входные параметры, по одному, и измеряет ответ системы к этому возмущению путем вычисления $δ \dot{x}$ и δy.
Вычисляет матрицы пространства состояний с помощью возмущения и ответа.

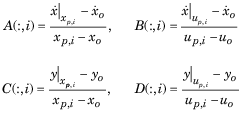
где

xp_{, i} - вектор состояния, ith компонент которого встревожен от значения рабочей точки.
xo является вектором состояния в рабочей точке.
_i - входной вектор, ith компонент которого встревожен от значения рабочей точки.
uo является входным вектором в рабочей точке.
${\dot{x} |}_{x_{p, i}}$ значение $\dot{x}$ в xp_{, i}, uo.
${\dot{x} |}_{u_{p, i}}$ значение $\dot{x}$ в_{, i}, xo.
${\dot{x}}_{o}$ значение $\dot{x}$ в рабочей точке.
${y |}_{x_{p, i}}$ значение $y$ в xp_{, i}, uo.
${y |}_{u_{p, i}}$ значение $y$ в_{, i}, xo.
эй значение y в рабочей точке.

Пользовательские блоки

Все определяемые пользователем блоки, такие как S-функция и блоки MATLAB function, совместимы с линеаризацией. Эти блоки линеаризуются с помощью числового возмущения.

Пользовательские блоки не линеаризуют, когда эти блоки используют недвойные типы данных точности.

Смотрите линеаризуют блоки с недвойными сигналами типа данных точности.

Ищите таблицы

Регулярный взгляд таблицы численно встревожен. Предварительные интерполяционные таблицы имеют предварительно запрограммированную (точную) линеаризацию блока блоком.

Документация