Разработайте оптимизацию, чтобы удовлетворить требования переходного процесса (код)

Этот пример показывает, как программно оптимизировать параметры контроллера, чтобы удовлетворить требования переходного процесса с помощью функции sdo.optimize.

Образцовая структура

Модель watertank_stepinput Simulink^® включает нелинейный Системный объект Бака для воды и контроллер PI в одноконтурной системе с обратной связью.

Блок Step применяет вход шага. Можно также использовать другие типы входа, такие как пандус, чтобы оптимизировать ответ, сгенерированный такими входными параметрами.

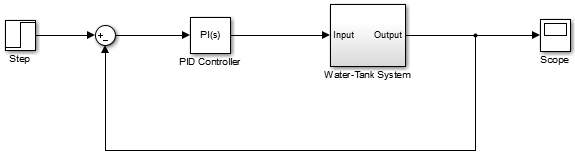
Эти данные показывают Систему Бака для воды.

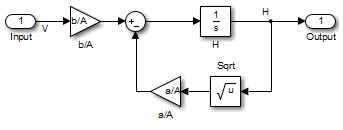
Вода вводит корпус наверху на уровне, пропорциональном открытию клапана. Открытие клапана пропорционально напряжению, V, применился к насосу. Вода уезжает посредством открытия в основе корпуса на уровне, который пропорционален квадратному корню из высоты воды, H. Присутствие квадратного корня в уровне потока воды приводит к нелинейному объекту.

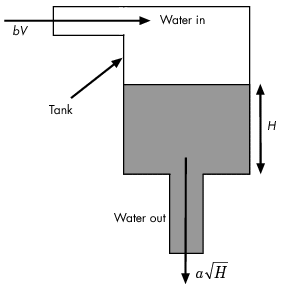
Следующая таблица описывает переменные, параметры, дифференциальные уравнения, состояния, входные параметры и выходные параметры Системы Бака для воды.

Переменные	H является высотой воды в корпусе. Vol является объемом воды в корпусе. V является напряжением, применился к насосу.
Параметры	A является площадью поперечного сечения корпуса. b является константой, связанной со скоростью потока жидкости в корпус. a является константой, связанной со скоростью потока жидкости из корпуса.
Дифференциальное уравнение	$\frac{d}{d t} V o l = A \frac{d H}{d t} = b V - a \sqrt{H}$
Состояния	H
Входные параметры	V
Выходные параметры	H

Конструктивные требования

Высота воды в корпусе, H, должна удовлетворить требования ответа следующего шага:

Время нарастания меньше чем 2,5 секунды
Время установления меньше чем 20 секунд
Перерегулирование меньше чем 5%

Задайте требования переходного процесса

Откройте модель Simulink.

sys = 'watertank_stepinput';
open_system(sys);

Регистрируйте уровень воды, H.
Во время оптимизации модель моделируется с помощью текущего значения параметров модели, и регистрируемый сигнал используется, чтобы оценить конструктивные требования.
```
PlantOutput = Simulink.SimulationData.SignalLoggingInfo;
PlantOutput.BlockPath               = [sys '/Water-Tank System'];
PlantOutput.OutputPortIndex         = 1;
PlantOutput.LoggingInfo.NameMode    = 1;
PlantOutput.LoggingInfo.LoggingName = 'PlantOutput';
```
Храните информацию журналирования.
```
simulator = sdo.SimulationTest(sys);
simulator.LoggingInfo.Signals = PlantOutput;
```
simulator является объектом sdo.SimulationTest, который вы также используете позже, чтобы моделировать модель.
Задайте требования переходного процесса.
```
StepResp = sdo.requirements.StepResponseEnvelope;
StepResp.RiseTime = 2.5;
StepResp.SettlingTime = 20;
StepResp.PercentOvershoot = 5;
StepResp.FinalValue = 2;
StepResp.InitialValue = 1;
```
StepResp является объектом sdo.requirements.StepResponseEnvelope. Значения, присвоенные StepResp.FinalValue и StepResp.InitialValue, соответствуют ступенчатому изменению в высоте бака для воды от 1 до 2.

Задайте переменные проекта

Когда вы оптимизируете образцовый ответ, программное обеспечение изменяет параметр (разработайте переменную), значения, чтобы соответствовать конструктивным требованиям.

Выберите параметры модели, чтобы оптимизировать. Здесь, оптимизируйте параметры ПИД-регулятора.
```
p = sdo.getParameterFromModel(sys,{'Kp','Ki'});
```
p является массивом 2 объектов param.Continuous.
Чтобы ограничить параметры положительными значениями, установите минимальное значение каждого параметра к 0.
```
p(1).Minimum = 0;
p(2).Minimum = 0;
```

Оптимизируйте образцовый ответ

Создайте функцию проекта, чтобы оценить производительность системы для набора значений параметров.
```
evalDesign = @(p) sldo_model1_design(p,simulator,StepResp);
```
evalDesign является анонимной функцией, которая вызывает функцию стоимости sldo_model1_design. Функция стоимости моделирует модель и оценивает конструктивные требования.
Совет
Введите edit sldo_model1_design, чтобы просмотреть эту функцию.
Оцените текущий ответ. (Необязательно)
1. Вычислите образцовый ответ с помощью текущих значений переменных проекта.
  initDesign = evalDesign(p);
  Во время симуляции блок Step Response выдает предупреждения утверждения в подсказке MATLAB^®, которые указывают, что требования, заданные в блоке, не удовлетворены.
2. Исследуйте нелинейные ограничения неравенства.
  initDesign.Cleq
  ans = 0.1739 0.0169 -0.0002 -0.0101 -0.0229 0.0073 -0.0031 0.0423
  Некоторые значения Cleq положительны вне заданного допуска, который указывает, что ответ с помощью текущих значений параметров нарушает конструктивные требования.
Задайте опции оптимизации.
```
opt = sdo.OptimizeOptions;
opt.MethodOptions.Algorithm = 'sqp';
```
Программное обеспечение конфигурирует opt, чтобы использовать метод оптимизации по умолчанию, fmincon и последовательный алгоритм квадратичного программирования для fmincon.
Оптимизируйте ответ.
```
[pOpt,optInfo] = sdo.optimize(evalDesign,p,opt);
```
В каждой итерации оптимизации программное обеспечение моделирует модель и решатель оптимизации по умолчанию, fmincon изменяет переменные проекта, чтобы соответствовать конструктивным требованиям. Для получения дополнительной информации смотрите, Как Алгоритм Оптимизации Формулирует проблемы Минимизации.
После того, как оптимизация завершается, командное окно отображает следующие результаты:
```
                               max        Step-size    First-order 
 Iter F-count        f(x)   constraint                 optimality
    0      5            0       0.1739
    1     10            0      0.03411            1         0.81
    2     15            0            0        0.235       0.0429
    3     15            0            0     2.26e-18            0
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the selected value of the function tolerance,
and constraints are satisfied to within the selected value of the constraint tolerance.
```
Local minimum found that satisfies the constraints сообщения указывает, что решатель оптимизации нашел решение, которое соответствует конструктивным требованиям в заданных допусках. Для получения дополнительной информации о выводах, отображенных во время оптимизации, смотрите Итеративное Отображение (Optimization Toolbox).
Исследуйте информацию о завершении оптимизации, содержавшуюся в выходном аргументе optInfo. Эта информация помогает вам проверить, что ответ удовлетворяет требования переходного процесса.
Например, проверяйте следующие поля:
- Cleq, который показывает оптимизированные нелинейные ограничения неравенства.
  optInfo.Cleq
  ans = -0.0001 -0.0028 -0.0050 -0.0101 -0.0135 -0.0050 -0.0050 -0.0732
  Все значения удовлетворяют Cleq ≤ 0 в допусках оптимизации, который указывает, что требования переходного процесса удовлетворены.
- exitflag, который идентифицирует почему отключенная оптимизация.
  Значением является 1, который указывает, что решатель нашел решение, которое было меньше, чем заданные допуски на ограничительных нарушениях и значении функции.

Просмотрите оптимизированные значения параметров.

pOpt

pOpt(1,1) =
 
       Name: 'Kp'
      Value: 2.0545
    Minimum: 0
    Maximum: Inf
       Free: 1
      Scale: 1
       Info: [1x1 struct]

 
pOpt(2,1) =
 
       Name: 'Ki'
      Value: 0.3801
    Minimum: 0
    Maximum: Inf
       Free: 1
      Scale: 1
       Info: [1x1 struct]

Моделируйте модель с оптимизированными значениями.
1. Обновите оптимизированные значения параметров в модели.
  sdo.setValueInModel(sys,pOpt);
2. Моделируйте модель.
  sim(sys);

Документация