Как алгоритм оптимизации формулирует проблемы минимизации

Когда вы оптимизируете параметры модели Simulink^®, чтобы соответствовать конструктивным требованиям, программное обеспечение Simulink Design Optimization™ автоматически преобразовывает требования в ограниченную задачу оптимизации и затем решает проблему с помощью методов оптимизации. Ограниченная задача оптимизации итеративно моделирует модель Simulink, сравнивает результаты симуляций с ограничительными целями и использует методы оптимизации, чтобы настроить настроенные параметры, чтобы лучше достигнуть целей.

Эта тема описывает, как программное обеспечение формулирует ограниченную задачу оптимизации, используемую алгоритмами оптимизации. Для каждого алгоритма оптимизации программное обеспечение формулирует один из следующих типов проблем минимизации:

Выполнимость
Отслеживание
Смешанная выполнимость и отслеживание

Для получения дополнительной информации о том, как каждый алгоритм оптимизации формулирует эти проблемы, см.:

Проблема выполнимости и ограничительная формулировка

Feasibility означает, что алгоритм оптимизации находит значения параметров, которые удовлетворяют все ограничения к в заданных допусках, но не минимизирует целевой функции или функции стоимости при этом.

В следующей фигуре x ₁, x ₃, и _xn представляет комбинацию значений параметров P ₁ и P ₂ и является выполнимыми решениями, потому что они не нарушают ограничение нижней границы.

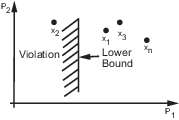
В модели Simulink вы ограничиваете сигнал путем определения нижних и верхних границ в блоке Check (Характеристики Переходного процесса Проверки...) или объект требования (sdo.requirements.StepResponseEnvelope...), как показано в следующей фигуре.

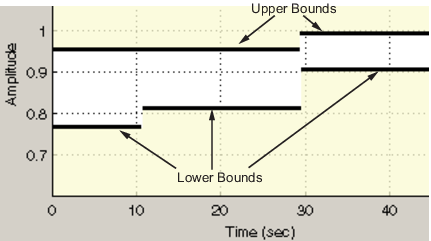
Этими ограничениями является piecewise linear bounds. Кусочный линейный связанный _ybnd с ребрами n может быть представлен как:

$y_{b n d} (t) = {\begin{matrix} y_{1} (t) & t_{1} \leq t \leq t_{2} \\ y_{2} (t) & t_{2} \leq t \leq t_{3} \\ ⋮ & ⋮ \\ y_{n} (t) & t_{n} \leq t \leq t_{n + 1} \end{matrix},$

Программное обеспечение вычисляет расстояние со знаком между моделируемым ответом и ребром. Расстояние со знаком для нижних границ:

$\begin{array}{l} c = [\begin{array}{l} \max_{t_{1} \leq t \leq t_{2}} y_{b n d} - y_{s i m} \\ \max_{t_{2} \leq t \leq t_{3}} y_{b n d} - y_{s i m} \\ \max_{t_{n} \leq t \leq t_{n + 1}} y_{b n d} - y_{s i m} \end{array}], \end{array}$

где _ysim является моделируемым ответом и является функцией оптимизируемых параметров.

Расстояние со знаком для верхних границ:

$c = [\begin{matrix} \max_{t_{1} \leq t \leq t_{2}} y_{s i m} - y_{b n d} \\ \max_{t_{2} \leq t \leq t_{3}} y_{s i m} - y_{b n d} \\ \max_{t_{n} \leq t \leq t_{n + 1}} y_{s i m} - y_{b n d} \end{matrix}] .$

В командной строке opt_fcn предоставляет c непосредственно от поля Cleq vals.

Если всем ограничениям соответствуют (c ≤ 0) для некоторой комбинации значений параметров, то то решение, как говорят, выполнимо. В следующей фигуре x ₁ и x ₃ является выполнимыми решениями.

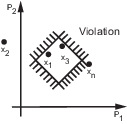
Когда ваша модель имеет несколько требований или векторных сигналов, питающих требование, ограничительный вектор расширен с ограничительными нарушениями для каждого сигнала и связан:

$C = [c_{1}; c_{2}; \dots; c_{n}] .$

Отслеживание проблемы

Кроме того, к нижним и верхним границам, можно задать ссылочный сигнал в блоке Check Against Reference или объекте sdo.requirements.SignalTracking, который модель Simulink может отследить вывод. Цель отслеживания является целью отслеживания квадратичной невязки суммы.

Вы задаете ссылочный сигнал как последовательность амплитудных временем пар:

$y_{r e f} (t_{r e f}), t_{r e f} \in {T_{r e f 0}, T_{r e f 1}, \dots, T_{r e f N}} .$

Программное обеспечение вычисляет моделируемый ответ как последовательность амплитудных временем пар:

$y_{s i m} (t_{s i m}), t_{s i m} \in {T_{s i m 0}, T_{s i m 1}, \dots, T_{s i m N}},$

где некоторые значения _tsim могут совпадать со значениями _tref.

Новая основа времени, _tnew, формируется из объединения элементов _tref и _tsim. Элементы, которые не являются в минимально-максимальной области значений и _tref и _tsim, не использованы:

$t_{n e w} = {t : t_{s i m} \cup t_{r e f}}$

Используя линейную интерполяцию, программное обеспечение вычисляет значения _yref и _ysim в то время точки в _tnew и затем вычисляет масштабированную ошибку:

$e (t_{n e w}) = \frac{(y_{s i m} (t_{n e w}) - y_{r e f} (t_{n e w}))}{\max_{t_{n e w}} | y_{r e f} |} .$

Наконец, программное обеспечение вычисляет взвешенную, интегральную квадратную ошибку:

$f = \int w (t) e {(t)}^{2} d t .$

Примечание

Вес w (t) равняется 1 по умолчанию. Можно задать различное значение веса только в командной строке.

Когда ваша модель имеет требования или векторные сигналы, питающие требование, цель отслеживания равняется сумме отдельных отслеживающих интегральных ошибок для каждого сигнала:

$F = \sum f_{i} .$

Проблемные формулировки метода спуска градиента

Метод Спуска Градиента использует функцию Optimization Toolbox™ fmincon, чтобы оптимизировать параметры модели, чтобы соответствовать конструктивным требованиям.

Проблемный тип	Проблемная формулировка
Проблема выполнимости	Программное обеспечение формулирует ограничение C (x), как описано в проблеме Выполнимости и Ограничительной Формулировке. Если вы выбираете максимально выполнимую опцию решения (т.е. оптимизация продолжается после того, как начальное выполнимое решение найдено), программное обеспечение использует следующую проблемную формулировку: $\begin{array}{l} \min_{[x, γ]} γ \\ s . t . C (x) \leq γ \\ \underline{x} \leq x \leq \bar{x} \\ γ \leq 0 \end{array}$ γ слабая переменная, которая разрешает выполнимое решение с C (x) ≤ γ, а не C (x) ≤ 0. Если вы не выбираете максимально выполнимую опцию решения (т.е. оптимизация останавливается, как только выполнимое решение найдено), программное обеспечение использует следующую проблемную формулировку: $\begin{array}{l} \min_{x} 0 \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$
Отслеживание проблемы	Программное обеспечение формулирует отслеживающий объективный F (x), как описано в Отслеживании проблемы и минимизирует цель отслеживания: $\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Смешанная проблема выполнимости и отслеживания	Программное обеспечение минимизирует следующую проблемную формулировку: $\begin{array}{l} \min_{x} F (x) \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$ Примечание При отслеживании ссылочного сигнала программное обеспечение игнорирует максимально выполнимую опцию решения.

Проблемный тип

Проблемная формулировка

Проблема выполнимости

Программное обеспечение формулирует ограничение C (x), как описано в проблеме Выполнимости и Ограничительной Формулировке.

Если вы выбираете максимально выполнимую опцию решения (т.е. оптимизация продолжается после того, как начальное выполнимое решение найдено), программное обеспечение использует следующую проблемную формулировку:
$\begin{array}{l} \min_{[x, γ]} γ \\ s . t . C (x) \leq γ \\ \underline{x} \leq x \leq \bar{x} \\ γ \leq 0 \end{array}$
γ слабая переменная, которая разрешает выполнимое решение с C (x) ≤ γ, а не C (x) ≤ 0.
Если вы не выбираете максимально выполнимую опцию решения (т.е. оптимизация останавливается, как только выполнимое решение найдено), программное обеспечение использует следующую проблемную формулировку:
$\begin{array}{l} \min_{x} 0 \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$

Отслеживание проблемы

Программное обеспечение формулирует отслеживающий объективный F (x), как описано в Отслеживании проблемы и минимизирует цель отслеживания:

$\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$

Смешанная проблема выполнимости и отслеживания

Программное обеспечение минимизирует следующую проблемную формулировку:

$\begin{array}{l} \min_{x} F (x) \\ s . t . C (x) \leq 0 \\ \underline{x} \leq x \leq \bar{x} \end{array}$

Примечание

При отслеживании ссылочного сигнала программное обеспечение игнорирует максимально выполнимую опцию решения.

Симплексные проблемные формулировки метода поиска

Симплексный Метод поиска использует функцию Optimization Toolbox fminsearch и fminbnd, чтобы оптимизировать параметры модели, чтобы соответствовать конструктивным требованиям. fminbnd используется, если один скалярный параметр оптимизируется, в противном случае fminsearch используется. Вы не можете использовать границы параметра $\underline{x} \leq x \leq \bar{x}$ с fminsearch.

Проблемный тип	Проблемная формулировка
Проблема выполнимости	Программное обеспечение формулирует ограничение C (x), как описано в проблеме Выполнимости и Ограничительной Формулировке и затем минимизирует максимальное ограничительное нарушение: $\min_{x} max (C (x))$
Отслеживание проблемы	Программное обеспечение формулирует отслеживающий объективный F (x), как описано в Отслеживании проблемы и затем минимизирует цель отслеживания: $\min_{x} F (x)$
Смешанная проблема выполнимости и отслеживания	Программное обеспечение формулирует проблему на двух шагах: Находит выполнимое решение. $\min_{x} max (C (x))$ Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве исходных предположений и поддерживает выполнимость путем представления прерывистого барьера в цели оптимизации. $\begin{array}{l} \min_{x} Γ (x) \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & в противном случае . \end{array} \end{array}$

Проблемный тип

Проблемная формулировка

Проблема выполнимости

Программное обеспечение формулирует ограничение C (x), как описано в проблеме Выполнимости и Ограничительной Формулировке и затем минимизирует максимальное ограничительное нарушение:

$\min_{x} max (C (x))$

Отслеживание проблемы

Программное обеспечение формулирует отслеживающий объективный F (x), как описано в Отслеживании проблемы и затем минимизирует цель отслеживания:

$\min_{x} F (x)$

Смешанная проблема выполнимости и отслеживания

Программное обеспечение формулирует проблему на двух шагах:

Находит выполнимое решение.
$\min_{x} max (C (x))$
Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве исходных предположений и поддерживает выполнимость путем представления прерывистого барьера в цели оптимизации.
$\begin{array}{l} \min_{x} Γ (x) \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & в противном случае . \end{array} \end{array}$

Проблемные формулировки метода поиска шаблона

Метод поиска Шаблона использует функцию Global Optimization Toolbox patternsearch, чтобы оптимизировать параметры модели, чтобы соответствовать конструктивным требованиям.

Проблемный тип	Проблемная формулировка
Проблема выполнимости	Программное обеспечение формулирует ограничение C (x), как описано в проблеме Выполнимости и Ограничительной Формулировке и затем минимизирует максимальное ограничительное нарушение: $\begin{array}{l} \min_{x} max (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Отслеживание проблемы	Программное обеспечение формулирует отслеживающий объективный F (x), как описано в Отслеживании проблемы и затем минимизирует цель отслеживания: $\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Смешанная проблема выполнимости и отслеживания	Программное обеспечение формулирует проблему на двух шагах: Находит выполнимое решение. $\begin{array}{l} \min_{x} max (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$ Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве исходных предположений и поддерживает выполнимость путем представления прерывистого барьера в цели оптимизации. $\begin{array}{l} \min_{x} Γ (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & в противном случае . \end{array} \end{array}$

Проблемный тип

Проблемная формулировка

Проблема выполнимости

$\begin{array}{l} \min_{x} max (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$

Отслеживание проблемы

$\begin{array}{l} \min_{x} F (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$

Смешанная проблема выполнимости и отслеживания

Программное обеспечение формулирует проблему на двух шагах:

Находит выполнимое решение.
$\begin{array}{l} \min_{x} max (C (x)) \\ s . t . \underline{x} \leq x \leq \bar{x} \end{array}$
Минимизирует цель отслеживания. Программное обеспечение использует результаты шага 1 в качестве исходных предположений и поддерживает выполнимость путем представления прерывистого барьера в цели оптимизации.
$\begin{array}{l} \min_{x} Γ (x) \\ s . t . \underline{x} \leq x \leq \bar{x} \\ где \\ Γ (x) = {\begin{array}{l} \infty & если \max (C (x)) > 0 \\ F (x) & в противном случае . \end{array} \end{array}$

Вычисления градиента

Для Gradient descent (fmincon) решатель оптимизации градиенты вычисляются с помощью числового возмущения:

$\begin{array}{l} d x = \sqrt[3]{e p s} \times \max (| x |, \frac{1}{10} x_{t y p i c a l}) \\ d L = \max (x - d x, x_{\min}) \\ d R = \min (x + d x, x_{\max}) \\ F_{L} = o p t_f c n (d L) \\ F_{R} = o p t_f c n (d R) \\ \frac{d F}{d x} = \frac{(F_{L} - F_{R})}{(d L - d R)} \end{array}$

x является скалярной переменной проекта.
_xmin является нижней границей x.
_xmax является верхней границей x.
_xtypical является масштабированным значением x.
opt_fcn является целевой функцией.

dx является относительно большим, чтобы разместить допуски решателя симуляции.

Если вы хотите вычислить градиенты каким-либо другим способом, можно сделать так в функции стоимости, которую вы пишете для выполнения оптимизации проекта программно. Смотрите sdo.optimize и GradFcn sdo.OptimizeOptions для получения дополнительной информации.

Документация