Квадратичные поверхности ответа являются простыми моделями, которые обеспечивают максимум или минимум, не делая дополнительные предположения о форме ответа. Квадратичные модели могут быть калиброваны с помощью полных планов факторного эксперимента с тремя или больше уровнями для каждого фактора, но эти проекты обычно требуют, чтобы больше выполнений, чем необходимый точно оценило параметры модели. В этом разделе рассматриваются проекты для калибровки квадратичных моделей, которые намного более эффективны, с помощью трех или пяти уровней для каждого фактора, но не используя все комбинации уровней.
Центральные составные проекты (CCD), также известные как проекты Вильсона Поля, подходят для калибровки полных квадратичных моделей. Существует три типа CCD — ограничены, нанесены, и стояли — изображенный ниже:
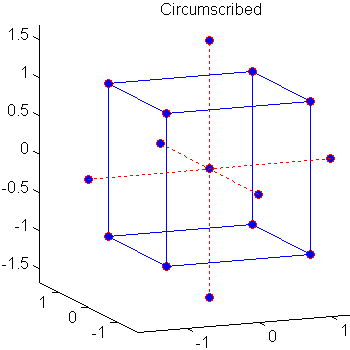
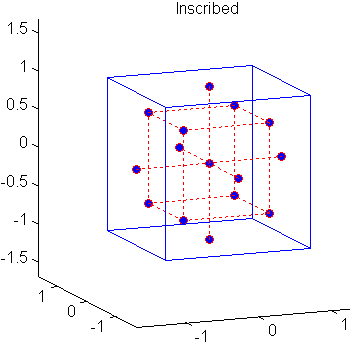
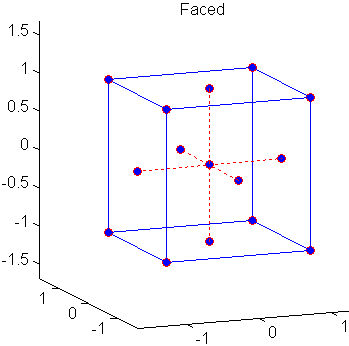
Каждый проект состоит из плана факторного эксперимента (углы куба) вместе с center и точками star, которые допускают оценку эффектов второго порядка. Для полной квадратичной модели с факторами n CCD имеют достаточно точек проекта, чтобы оценить (n +2) (n +1)/2 коэффициенты в полной квадратичной модели с факторами n.
Тип используемого CCD (положение факториальных и звездообразных точек) определяется рядом факторов и желаемыми свойствами проекта. Следующая таблица обобщает некоторые важные свойства. Проектом является rotatable, если отклонение прогноза зависит только от расстояния точки проекта от центра проекта.
| Проект | Поворотный | Факторные уровни | Точки использования вне ±1 | Точность оценок |
|---|---|---|---|---|
| Ограниченный (CCC) | Да | 5 | Да | Хороший по целому пробелу проекта |
| Нанесенный (CCI) | Да | 5 | Нет | Хороший по центральному подмножеству пробела проекта |
| Облицованный (CCF) | Нет | 3 | Нет | Ярмарка по целому пробелу проекта; плохой для коэффициентов неполного квадратного уравнения |
Сгенерируйте CCD с функцией Statistics and Machine Learning Toolbox™ ccdesign:
dCC = ccdesign(3,'type','circumscribed')
dCC =
-1.0000 -1.0000 -1.0000
-1.0000 -1.0000 1.0000
-1.0000 1.0000 -1.0000
-1.0000 1.0000 1.0000
1.0000 -1.0000 -1.0000
1.0000 -1.0000 1.0000
1.0000 1.0000 -1.0000
1.0000 1.0000 1.0000
-1.6818 0 0
1.6818 0 0
0 -1.6818 0
0 1.6818 0
0 0 -1.6818
0 0 1.6818
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0Повторные выполнения центральной точки допускают более универсальную оценку отклонения прогноза по целому пробелу проекта.
Как проекты, описанные в Центральных Составных Проектах, проекты Поля-Behnken используются, чтобы калибровать полные квадратичные модели. Проекты поля-Behnken являются поворотными и, для маленького ряда факторов (четыре или меньше), требуют меньшего количества выполнений, чем CCD. Путем предотвращения углов пробела проекта они позволяют экспериментаторам работать вокруг экстремальных факторных комбинаций. Как нанесенный CCD, однако, затем плохо оцениваются экстремальные значения.
Геометрия проекта Поля-Behnken изображена в следующей фигуре.
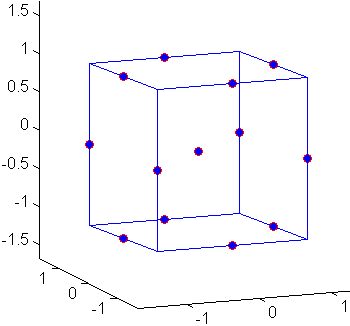
Разработайте точки, в средних точках ребер пробела проекта и в центре и не содержат встроенный план факторного эксперимента.
Сгенерируйте проекты Поля-Behnken с функцией Statistics and Machine Learning Toolbox bbdesign:
dBB = bbdesign(3)
dBB =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0Снова, повторные выполнения центральной точки допускают более универсальную оценку отклонения прогноза по целому пробелу проекта.