Dom:: UnivariatePolynomialОбласти одномерных полиномов
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Dom::UnivariatePolynomial(<Var, <R, <Order>>>)Dom::UnivariatePolynomial(Var, R, Order)(p)Dom::UnivariatePolynomial(Var, R, Order)(lm)Dom::UnivariatePolynomial(Var, R, ..) создает область одномерных полиномов в переменной Var по коммутативному кольцевому R.
Dom::UnivariatePolynomial представляет одномерные полиномы по произвольным коммутативным звонкам.
Все обычные алгебраические и арифметические полиномиальные операции реализованы, включая базисные вычисления Gröbner.
Dom::UnivariatePolynomial(Var, R, Order) создает область одномерных полиномов в переменной Var по области категории Cat::CommutativeRing в разреженном представлении относительно одночлена, заказывая Order.
Dom::UnivariatePolynomial() создает одномерную полиномиальную область в переменной x по доменному Dom::ExpressionField (normal) относительно лексикографического одночленного упорядоченного расположения.
Dom::UnivariatePolynomial(Var) создает одномерную полиномиальную область в переменной Var по доменному Dom::ExpressionField (normal) относительно лексикографического одночленного упорядоченного расположения.
Только коммутативные содействующие звонки типа DOM_DOMAIN, которые наследовались Dom::BaseDomain, позволены. Если R будет иметь тип DOM_DOMAIN, но наследуется не Dom::BaseDomain, доменный Dom::ExpressionField, ТО (normal) будет использоваться вместо этого.
Для этой области только идентификаторы являются действительными переменными.
Это, настоятельно рекомендуют использовать только содействующие звонки с уникальным нулевым представлением. В противном случае это может произойти, который, например, не отключит полиномиальное деление, или будет возвращена неправильная степень.
Обратите внимание на то, что по причинам эффективности не все методы проверяют свои аргументы, даже на интерактивном уровне. В частности это верно для многих методов доступа, преобразовывая методы и технические методы. Поэтому использование этих методов неуместно может привести к странным сообщениям об ошибке.
Если R имеет Ax::normalRep, то Ax::normalRep.
Если R имеет Ax::canonicalRep, то Ax::canonicalRep.
Чтобы создать звонок одномерных полиномов в x по целым числам, можно задать
UP:=Dom::UnivariatePolynomial(x,Dom::Integer)
![]()
Теперь, давайте создадим два одномерных полинома.
a:=UP((2*x-1)^2*(3*x+1))
![]()
b:=UP(((2*x-1)*(3*x+1))^2)
![]()
Обычные арифметические операции для полиномов доступны:
a^2+a*b
![]()
Ведущий коэффициент, ведя термин, ведущий одночлен и reductum a
lcoeff(a),lterm(a),lmonomial(a),UP::reductum(a)
![]()
и a имеет степень
degree(a)
![]()
Метод gcd вычисляет наибольший общий делитель двух полиномов
gcd(a,b)
![]()
и lcm наименьшее общее кратное:
lcm(a,b)
![]()
Вычисление определенного и неопределенного интеграла полинома также возможно,
int(a)
![]()
который является в случае неопределенного интегрирования просто антипроизводной полинома.
D(int(a)), domtype(D(int(a)))

Но, с тех пор для представления неопределенного интеграла a содействующий звонок, выбранный в качестве целых чисел, не является соответствующим, полиномиальный звонок по его полю частных используется вместо этого.
Кроме того, интерпретация полиномов как полиномиальные функции также позволена в применении содействующих кольцевых элементов, полиномов этот доменные или произвольные выражения с опцией Expr им:
a(5)
![]()
a(b)
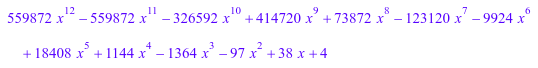
a(sin(x),Expr)
![]()
Чтобы получить вектор коэффициентов полинома, который дает плотное представление его, можно использовать метод vectorize.
UP::vectorize(a), UP::vectorize(a,6)
![]()
|
Неопределенное, данное идентификатором; значением по умолчанию является |
|
Коммутативный звонок, т.е. область категории |
|
Одночленное упорядоченное расположение, т.е. одно из предопределенных упорядоченных расположений |
|
Полином или многочленное выражение. |
|
Список одночленов, которые представлены как списки, содержащие коэффициенты вместе с векторами экспоненты или экспонентами. |
| "характеристика" | Характеристика этой области. |
| "coeffRing" | Содействующий звонок этой области, как задано параметром |
| "ключ" | Имя области создается. |
| "один" | Нейтральный элемент w.r.t. |
| "упорядоченное расположение" | Одночленный порядок, как задано параметром |
| Переменные | Список переменной, как задано параметром |
| "нуль" | Нейтральный элемент w.r.t. |