fourierПреобразование Фурье
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
fourier(f, t, w)
fourier(f, t, w) вычисляет преобразование Фурье выражения f = f(t) относительно переменной t в точке w и задан можно следующим образом:
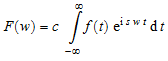 .
.
c и s являются параметрами преобразования Фурье. По умолчанию, c = 1 и s = -1.
Чтобы изменить параметры c и s преобразования Фурье, используйте Pref::fourierParameters. Смотрите Пример 3. Общий выбор для параметра c равняется 1![]() , или
, или![]() . Общий выбор для параметра
. Общий выбор для параметра s-1, 1, - 2 π или 2 π.
Если fourier не может найти явное представление преобразования, он возвращает неоцененный вызов функции. Смотрите Пример 4.
Если f является матрицей, fourier применяет преобразование Фурье ко всем компонентам матрицы.
Чтобы вычислить обратное преобразование Фурье, используйте ifourier.
Чтобы вычислить дискретное преобразование Фурье, используйте numeric::fft.
Результаты, возвращенные fourier, зависят от текущих настроек Pref::fourierParameters.
Вычислите преобразование Фурье этого выражения относительно переменной t:
fourier(exp(-t^2), t, w)
![]()
Вычислите преобразование Фурье этого выражения относительно переменной t для положительных значений параметра w 0:
assume(w_0 > 0): F := fourier(t*exp(-w_0^2*t^2), t, w)
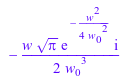
Оцените преобразование Фурье выражения в точках w = 2 w0 и w = 5. Можно выполнить получившееся выражение F с помощью | (или его функциональная форма evalAt):
F | w = 2*w_0
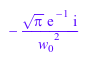
Кроме того, можно оценить преобразование Фурье в конкретной точке непосредственно:
fourier(t*exp(-w_0^2*t^2), t, 5)

Параметрами по умолчанию преобразования Фурье является c = 1 и s = -1.
fourier(t*exp(-t^2), t, w)
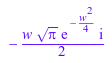
Чтобы изменить эти параметры, используйте Pref::fourierParameters прежде, чем вызвать fourier:
Pref::fourierParameters(1, 1):
Оцените преобразование того же выражения с новыми параметрами:
fourier(t*exp(-t^2), t, w)

Для дальнейших вычислений восстановите значения по умолчанию параметров преобразования Фурье:
Pref::fourierParameters(NIL):
Если fourier не может найти явное представление преобразования, он отвечает на неоцененный звонок:
fourier(besselJ(1, 1/(1 + t^2)), t, w)
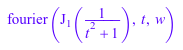
ifourier возвращает исходное выражение:
ifourier(%, w, t)
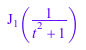
Вычислите следующие преобразования Фурье, которые вовлекают Дирака и функции Heaviside:
fourier(t^3, t, w)
![]()
fourier(heaviside(t - t_0), t, w)
![]()
Преобразование Фурье функции связано с преобразованием Фурье своей производной:
fourier(diff(f(t), t), t, w)
![]()
|
Арифметическое выражение или неоцененный вызов функции типа |
|
Идентификатор или индексированный идентификатор, представляющий переменную преобразования |
|
Арифметическое выражение, представляющее точку оценки |
Арифметическое выражение или матрица таких выражений
f
Ф. Обереттингер, “Таблицы преобразований Фурье и преобразований Фурье дистрибутивов”, Спрингер, 1990.