gcdexРасширенный Алгоритм Евклида для полиномов
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
gcdex(p,q, <x>) gcdex(f,g,x)
gcdex(p, q, x) расценивает p и q как одномерные полиномы в x и возвращает их наибольший общий делитель как линейную комбинацию p и q.
gcdex(p, q, x) возвращает последовательность g, s, t с тремя элементами, где полиномиальный g является наибольшим общим делителем p и q. Полиномы s и t удовлетворяют g = s p + t q и deg (s) <deg (q), deg (t) <deg (p). Эти данные вычисляются расширенным Алгоритмом Евклида.
gcdex только процессы одномерные полиномы:
Если неопределенный x задан, входные полиномы рассматриваются как одномерные полиномы в x.
Если не неопределенный задан, неопределенный из полиномов разыскивается внутренне. Ошибка происходит, если больше чем один неопределенный найден.
Обратите внимание на то, что x должен быть задан, если многочленные выражения используются на входе.
Многочленные выражения преобразованы в полиномы. Смотрите poly для деталей. FAIL возвращен, если аргумент не может быть преобразован в полином.
Возвращенные полиномы являются многочленными выражениями, если вход состоит из многочленных выражений. В противном случае полиномы типа DOM_POLY возвращены.
Содействующий звонок полиномов должен предоставить методу "_divide". Этот метод должен возвратить FAIL, если доменные элементы не могут быть разделены.
Если содействующая область полинома не является полем, то не может быть возможно представлять наибольший общий делитель как линейную комбинацию входных полиномов. В таком случае повышена ошибка.
Наибольший общий делитель двух одномерных полиномов в расширенной форме может быть вычислен можно следующим образом:
gcdex(poly(x^3 + 1), poly(x^2 + 2*x + 1))
![]()
Для многомерных полиномов должно быть задано неопределенное:
gcdex(poly(x^2*y), poly(x + y), x)
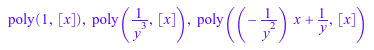
gcdex(poly(x^2*y), poly(x + y), y)
![]()
gcdex(x^3 + a, x^2 + 1, x)
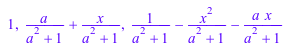
| |
| |
|
Неопределенное: идентификатор или индексируемый идентификатор |
Последовательность трех полиномов, или последовательность трех многочленных выражений или FAIL.
p, q