divideРазделите полиномы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
divide(p,q, <[x]>, <order>,options) divide(p,q, <[x1, x2, …]>, <order>,options) divide(p,q1, q2, …, <order>,options)
divide(p, q) делит полиномы или многочленные выражения p и q. По умолчанию функция возвращает частное s и остаток r, такой что p = s q + r. Здесь degree (r) <degree (q).
divide (p, q 1, q 2, q 3, …, q n) делит полином или многочленное выражение p полиномами или многочленными выражениями q 1, q 2, q 3, …, q n. Функция возвращает частных s 1, s 2, s 3, …, s n и остаток r, такой что p = s 1 q1 + s 2 q2 + s 3 q3 + … + s 4 q4 + r. Здесь ведущий коэффициент остатка r не может быть разделен на ведущие коэффициенты ни одного из делителей q 1, q 2, q 3, …, q n.
divide(p, q) делит многочленное или многочленное выражение p на многочленное или многочленное выражение q. Используйте опцию Quo, чтобы возвратить частное только. Используйте опцию Rem, чтобы возвратить остаток только.
Функция divide работает с полиномами или многочленными выражениями.
Полиномы должны иметь тот же тип: их переменные и содействующие звонки должны быть идентичными.
Когда вы вызываете divide для многочленных выражений, MuPAD® внутренне преобразовывает эти выражения в полиномы. Смотрите, что poly функционирует. Если вы не задаете список indeterminates, divide обрабатывает все символьные переменные в выражениях как indeterminates. Если выражения не могут быть преобразованы в полиномы, функция divide возвращает FAIL. Смотрите Пример 1.
Если вы вызываете divide для полиномов, он возвращает полиномы. Если вы вызываете divide для многочленных выражений, функция возвращает многочленные выражения. Смотрите Пример 2.
Если вы делите многочленные выражения, которые содержат больше чем одну переменную, можно задать конкретные переменные, которые будут обработаны как переменные. Функция divide обрабатывает все другие переменные как символьные параметры. По умолчанию divide принимает, что все переменные в многочленных выражениях являются переменными, и ни один из них не символьный параметр. Смотрите Пример 3.
divide (p, q 1, q 2, q 3, …, q n) делит полином или многочленное выражение p полиномами или многочленными выражениями q 1, q 2, q 3, …, q n. Функция возвращает частных s 1, s 2, s 3, …, s n и остаток r, такой что p = s 1 q1 + s 2 q2 + s 3 q3 + … + s 4 q4 + r. Здесь ведущий коэффициент остатка r не может быть разделен на ведущие коэффициенты ни одного из делителей q 1, q 2, q 3, …, q n. Смотрите Пример 6.
При делении полинома на один или несколько полиномов можно выбрать термин упорядоченное расположение. Упорядоченное расположение принимает следующие значения:
LexOrder устанавливает лексикографическое упорядоченное расположение.
DegreeOrder устанавливает общее упорядоченное расположение степени. При использовании этого упорядоченного расположения MuPAD сортирует условия полинома согласно общей степени каждого термина (сумма экспонент переменных).
DegInvLexOrder устанавливает общую инверсию степени лексикографическое упорядоченное расположение. При использовании этого упорядоченного расположения MuPAD сортирует условия полинома согласно общей степени каждого термина (сумма экспонент переменных). Если несколько условий имеют равные общие степени, MuPAD сортирует их использующий обратное лексикографическое упорядоченное расположение.
ваше пользовательское упорядоченное расположение термина типа Dom::MonomOrdering.
Содействующий звонок полиномов должен реализовать метод "_divide". MuPAD использует этот метод внутренне, чтобы разделить коэффициенты. Если коэффициенты не могут быть разделены, этот метод должен возвратить FAIL.
Для многочленных выражений divide внутренне вызывает функцию poly, которая преобразовывает выражение в полином. Если вы не задаете неопределенное из выражения, MuPAD принимает, что все переменные являются indeterminates. Например, функция divide не может разделить следующие многочленные выражения, потому что она принимает, что и x и y являются indeterminates:
divide(x/y, x)
![]()
Если вы указываете, что только x является неопределенным, результат:
divide(x/y, x, [x])
![]()
divide делит полиномы или многочленные выражения. Когда вы делите полиномы, функция возвращает полиномы:
divide(poly(x^3 + x + 1, [x]), poly(x^2 + x + 1, [x]))
![]()
Когда вы делите многочленные выражения, MuPAD внутренне преобразовывает эти выражения в полиномы, делит эти полиномы, и затем преобразовывает результат деления к многочленным выражениям:
divide(x^3 + x + 1, x^2 + x + 1)
![]()
При делении многомерных полиномов можно задать список переменных. Функция divide принимает, что все другие переменные являются символьными параметрами. Например, разделите следующие два многочленных выражения, указывающие, что и x и y являются переменными:
divide(x^2 - 2*x - y, y*x - 1, [x, y])
![]()
Разделите те же многочленные выражения, указывающие, что только x является переменной. MuPAD принимает, что y является символьным параметром:
divide(x^2 - 2*x - y, y*x - 1, [x])
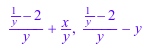
Теперь, разделите эти выражения, указывающие, что только y является переменной. MuPAD принимает, что x является символьным параметром:
divide(x^2 - 2*x - y, y*x - 1, [y])
![]()
По умолчанию функция divide обрабатывает многочленные выражения больше чем с одной переменной как многомерные многочленные выражения. Функция не принимает, что любая из переменных является символьными параметрами:
divide(x^2 - 2*x - y, y*x - 1)
![]()
По умолчанию divide возвращает частное и остаток от деления полиномов:
divide(x^3 + x + 1, x^2 + x + 1)
![]()
Чтобы возвратить частное только, используйте опцию Quo:
divide(x^3 + x + 1, x^2 + x + 1, Quo)
![]()
Чтобы возвратить остаток только, используйте опцию Rem:
divide(x^3 + x + 1, x^2 + x + 1, Rem)
![]()
Предположим, вы хотите получить результат деления только, когда деление без остатка возможно. Чтобы возвратить частное s деления без остатка полиномов или многочленных выражений, используйте опцию Exact:
divide(x^4 + 12*x^3 + 28*x^2 + 204*x + 187, x + 11, Exact)
![]()
Когда деление без остатка без остатка невозможно, функция divide с опцией Exact возвращает FAIL:
divide(x^4 + 12*x^3 + 28*x^2 + 204*x + 187, x + 12, Exact)
![]()
Функция divide позволяет вам делить полином (или многочленное выражение) несколькими полиномами (или многочленные выражения):
divide(4*x^4 + 2*x^2 + 1, x^3 - x + 1, x - 1)
![]()
При делении полинома на несколько полиномов можно выбрать термин упорядоченное расположение:
divide(x^2+y^3+1, x-y^2, y, LexOrder)
![]()
divide(x^2+y^3+1, x-y^2, y, DegreeOrder)
![]()
|
Одномерные или многомерные полиномы или многочленные выражения. |
|
Одномерные или многомерные полиномы или многочленные выражения. |
|
Неопределенный из полинома: обычно, идентификатор или индексируемый идентификатор. |
|
indeterminates полинома: обычно, идентификаторы или индексированные идентификаторы. |
|
Термин, заказывающий при делении одного многомерного полинома на один или несколько многомерных полиномов: |
|
Возвратите частное |
|
Возвратите частное |
Полином, многочленное выражение, последовательность полиномов или многочленных выражений или значения FAIL.
p, q