hypergeomГипергеометрические функции
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
hypergeom([a1, a2, …], [b1, b2, …], z)
hypergeom([a1, a2, ...], [b1, b2, ...], z) представляет гипергеометрическую функцию.
Гипергеометрическая функция задана для сложных аргументов a i, b j и z.
С a = [a 1, a 2, …, a p] и b = [b 1, b 2, …, b q], гипергеометрическая функция порядка p, q задан как
,
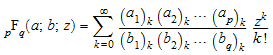где (c) k = c (c + 1) … (c + k - 1), (c) 0 = 1 является обычным символом Pochhammer. Количества a и b называются ‘списками для верхних и более низких параметров’, соответственно.
Значение с плавающей точкой возвращено, если по крайней мере один из аргументов является числом с плавающей запятой, и все другие аргументы могут быть преобразованы в числа с плавающей запятой.
Для большинства точных аргументов гипергеометрическая функция возвращает символьный вызов функции. Если верхний параметр совпадает с более низким параметром, эти значения отменяют и удалены из списков параметров.
Следующие специальные значения реализованы:
если список верхних параметров, a содержит больше, обнуляет, чем список более низких параметров b.
.
Если после отмены идентичных параметров верхние параметры содержат отрицательное целое число, больше, чем самое большое отрицательное целое число в более низких параметрах, то
полином в z. Если все верхние и более низкие параметры, а также аргумент z не содержат символьных идентификаторов, соответствующий явный результат возвращен. Если параметры или z содержат символы, расширение на полиномиальное представление доступно через simplify. Cf. Пример 2.
Также пустые списки a = [] или b = [] могут быть переданы hypergeom. Соответствующие функции:
,
,
.
Когда названо аргументами с плавающей точкой, эти функции чувствительны к переменной окружения DIGITS, который определяет числовую рабочую точность.
На символьные звонки отвечают для точных или символьных аргументов:
hypergeom([], [2], x), hypergeom([1], [2, 3], PI), hypergeom([1, 1/2], [1/3], x + 3*I)
Значения с плавающей точкой возвращены для аргументов с плавающей точкой:
hypergeom([], [2], 3.0), hypergeom([1], [2.0], PI), hypergeom([PI], [2, 3], 4.0), hypergeom([1, 2], [3, 4, 5, 6], 1.0*I), hypergeom([1 + I], [1/(2 + I)], 1.0*I)
равно
:
hypergeom([], [], z)
Поскольку идентичные значения в a и отмене b, то же самое верно для
:
hypergeom([a, b], [a, b], z)
Любая гипергеометрическая функция, выполненная в 0, имеет значение 1:
hypergeom([a, b], [c, d, e], 0)
Если после отмены идентичных параметров список верхних параметров содержит нуль, получившаяся гипергеометрическая функция является постоянной со значением 1:
hypergeom([0, 0, 2, 3], [a, 0, 4], z)
Если после отмены идентичных параметров верхние параметры содержат отрицательное целое число, больше, чем самое большое отрицательное целое число в более низких параметрах, гипергеометрическая функция является полиномом. Если все параметры, а также аргумент z являются числовыми, соответствующее явное значение возвращено:
hypergeom([-4, -2 , 3], [-3, 1, 4], PI*sqrt(2))
Для символьных параметров или символьного z, полиномиальное представление может быть получено через simplify или Simplify:
hypergeom([-40, -5], [1, 4], z) = simplify(hypergeom([-40, -5], [1, 4], z))
hypergeom([-3, a], [b], z) = Simplify(hypergeom([-3, a], [b], z))
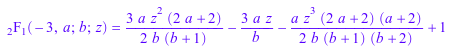
Если самое большое отрицательное целое число в списке более низких параметров больше, чем самое большое отрицательное целое число в списке верхних параметров, соответствующая гипергеометрическая функция не задана (потому что ее определение включает деление на нуль):
hypergeom([-40, -5, 3], [-3, 1, 4], z)
Error: Invalid arguments. [hypergeom]
Функции float, diff и series обрабатывают выражения, включающие гипергеометрические функции:
float(ln(3 + hypergeom([17], [exp(1), ln(5)], sqrt(PI))))
diff(hypergeom([a, b], [c, d], x), x)
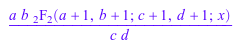
Обратите внимание на то, что дифференцирование гипергеометрической функции w.r.t. один из ее верхних или более низких параметров, в целом, не приводит к гипергеометрическим функциям. Определенные специфические случаи являются исключением:
diff(hypergeom([a + 1, b], [a + 2], x), a)
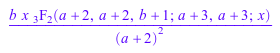
series(hypergeom([1, 2], [3], x), x)
Расширения о infinity возможны:
series(hypergeom([1/2], [1/3], x), x = infinity, 3)
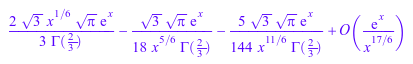
Однако существуют очень немногие (если таковые имеются) полные расширения для гипергеометрических функций о любом из его верхних или более низких параметров.
Часто, по конкретному выбору параметров, гипергеометрическая функция уменьшает до более простых специальных функций. Например, в случае
, также известный как стандартную вырожденную гипергеометрическую функцию, гипергеометрическая функция может уменьшаться до Функции Бесселя, если ее (один) более низкий параметр является точно дважды ее (одним) верхним параметром. Это проверяется численно ниже:
v:= 1.0 + I: z:= float(PI): hypergeom([v + 1/2], [2*v + 1], 2*I*z) = (gamma(1 + v)*exp(I*z)*((z/2)^(-v))*besselJ(v, z))
delete v, z:
В следующем примере
, который известен как гипергеометрическую функцию Гаусса, может уменьшаться в простую элементарную функцию включающие логарифмы, когда параметрами является [1, 1], [2], как проверено численно ниже:
eq := hypergeom([1, 1], [2], z) = -ln(1 - z)/z: float(subs(eq, z = 1/3)), float(subs(eq, z = 1/2))
delete eq:
Интервал
является разрезом для гипергеометрической функции; знак мнимой части изменяется при пересечении сокращения. Разрез принадлежит более низкому ответвлению:
eq := hypergeom([1, 1], [2], z) = -ln(1 - z)/z: float(subs(eq, z = 2 + I*10^(-DIGITS)))
float(subs(eq, z = 2 - I*10^(-DIGITS)))
float(subs(eq, z = 2))
|
‘Верхние параметры’: арифметические выражения |
|
‘Более низкие параметры’: арифметические выражения |
|
'Аргумент': арифметическое выражение |
Арифметическое выражение.
z
Когда никакой j b в списке b не находится в наборе {0, - 1, - 2, …}, ряд
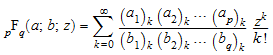
сходится, если одно из следующих условий содержит:
p ≤ q, |z | <∞;
p = q + 1, |z | <1;
p = q + 1, |z | = 1, ℜ (ψ q)> 0;
;
a содержит нуль или отрицательное целое число;
где
. Ряд отличается в остающихся случаях. Если один из параметров в isequal a, чтобы обнулить или отрицательное целое число, то ряд останавливается, превращаясь в то, что называется гипергеометрическим полиномом.
Обобщенная гипергеометрическая функция порядка (p, q) дана серийным определением в области сходимости, в то время как для p = q + 1, |z | ≥ 1, это задано как аналитическое продолжение этого ряда.
Функция
является симметричным w.r.t. параметры, т.е. это не зависит от порядка расположения a 1, a 2, … в a или b 1, b 2, … в b.
Как упомянуто выше, если некоторый верхний параметр равен n = 0, - 1, - 2, …, функция превращается в полином степени n. Если мы ослабляем условие, вышеизложенное для более низких параметров b и существует некоторый более низкий параметр, равный m = 0, - 1, - 2, …, функция
также уменьшает до полинома в z, обеспеченном n> m. Это не определено, если m> n или если никакой верхний параметр не является неположительным целым числом (приводящий к делению на нуль в одном из серийных коэффициентов). Случай m = n обработан следующим правилом.
Если для значений r верхних параметров, существуют значения r более низких параметров, равных им (т.е. a = [a 1, …, a p - r, c 1, …, c r], b = [b 1, …, b q - r, c 1, …, c r]), то порядок (p, q) функции
уменьшается до (p - r, q - r):
.
Вышеупомянутое правило применяется, даже если какой-либо i c, оказывается, нуль или отрицательное целое число (для получения дополнительной информации смотрите Люка в списке ссылок, p. 42).
удовлетворяет дифференциальному уравнению в z:
,
где (δ + a) и (δ + b) обозначают
и
, соответственно. Таким образом порядком этого дифференциального уравнения является max (p, q + 1), и гипергеометрическая функция является только одним из своих решений. Если p <q + 1, это дифференциальное уравнение имеет регулярную особенность в z = 0 и неправильную особенность в z = ∞. Если p = q + 1, точки z = 0, z = 1, и z = ∞ является регулярными особенностями, таким образом объясняя свойства сходимости гипергеометрического ряда.
Аналитическое продолжение для p = q + 1, |z | ≥ 1, задан путем выбора основного ответвления этого продолжения (также обозначенный как
) удовлетворение условия |arg (1 - z) | <π, сокращение вперед [1, ∞) чертится в комплексном z - плоскость. В частности, аналитическое продолжение может быть получено посредством интегрального представления (для получения дополнительной информации смотрите Прудникова и др. в ссылках), или функцией Майера Г.
[1] Люк, Y.L. “Специальные функции и их приближения”, издание 1, Academic Press, Нью-Йорк, 1969.
[2] Прудников, A.P., Ю. А. Брычков и О.И. Маричев, “Интегралы и ряд”, издание 3: более специальные функции, Гордон и нарушение, 1990.
[3] Abramowitz, M. и И.А. Стегун, “Руководство Математических функций”, Дуврские Публикации, Нью-Йорк, 9-я печать, 1970.