`indets`

Indeterminates выражения

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

indets(object)
indets(object, <All>)
indets(object, <PolyExpr>)
indets(object, <RatExpr>)

Описание

indets(object) возвращает indeterminates, содержавшийся в object.

indets(object) возвращает indeterminates object как набор, т.е. идентификаторы без значения, которые происходят в object, за исключением тех идентификаторов, происходящих в 0 th операнд подвыражения object (см. Пример 1).

indets расценивает специальные идентификаторы PI, EULER, CATALAN как indeterminates, несмотря на то, что они представляют постоянные вещественные числа. Если вы хотите исключить эти специальные идентификаторы, используйте indets(object) minus Type::ConstantIdents (см. Пример в качестве примера 1).

Если object является полиномом, функциональной средой, процедурой или встроенное ядро функция, то indets возвращает пустое множество. Смотрите Пример 2.

Примеры

Пример 1

Рассмотрите следующее выражение:

delete g, h, u, v, x, y, z:
e := 1/(x[u] + g^h) - f(1/3) + (sin(y) + 1)^2*PI^3 + z^(-3)*v^(1/2)

indets(e)

Обратите внимание на то, что возвращенный набор содержит x и u и не, как каждый может, ожидают, x[u], поскольку внутренне x[u] преобразован в функциональную форму _index(x, u). Кроме того, идентификатор, f не рассматривается неопределенным, поскольку это - 0 th операнд подвыражения f(1/3).

Несмотря на то, что PI математически представляет константу, это рассматривается неопределенным indets. Используйте Type::ConstantIdents, чтобы обойти это:

indets(e) minus Type::ConstantIdents

Результат indets существенно отличается, если одна из этих двух опций RatExpr или PolyExpr задана:

indets(e, RatExpr)

Действительно, e является рациональным выражением в “indeterminates” z, PI, sin(y), g^h, x[u], v^(1/2): e создается из этих атомов и константного выражения f(1/3) только при помощи рациональных операций +, -, *, / и ^ с целочисленными экспонентами. Точно так же e создается из PI,sin(y),z^(-3),1/(g^h+x[u]),v^(1/2) и константного выражения f(1/3) с помощью только полиномиальные операции +, -, * и ^ с неотрицательными целочисленными экспонентами:

indets(e, PolyExpr)

Пример 2

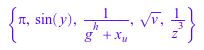
indets также работает на различные другие типы данных. Полиномы и функции, как рассматривается, не имеют никакого indeterminates:

delete x, y:
indets(poly(x*y, [x, y])), indets(sin), indets(x -> x^2+1)

Для контейнерных объектов indets возвращает объединение indeterminates всех записей:

indets([x, exp(y)]), indets([x, exp(y)], PolyExpr)

Для таблиц только возвращены indeterminates записей; indeterminates в индексах проигнорированы:

indets(table(x = 1 + sin(y), 2 = PI))

Пример 3

В предыдущих примерах мы видели, что 0 th операнд подвыражения не используется для нахождения indeterminates. С опцией All это изменяется:

delete x: e := sin(x):
indets(e, All)

Более комплексный пример:

delete g, h, u, v, y, z:
e := 1/(x[u] + g^h) - f(1/3) + (sin(y) + 1)^2*PI^3 + z^(-3)*v^(1/2)

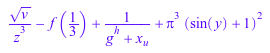
indets(e,All)

delete e:

Параметры

object

Произвольный объект

Опции

All

Идентификаторы, происходящие в 0 th операнд подвыражения object, также включены в результат.

При использовании этой опции 0 th операнд подвыражения не исключен из поиска indeterminates object. Таким образом, если 0 th операнд подвыражения является неопределенным, например, как sin это включено в результат, Cf. Пример 3.

PolyExpr

Возвратите набор арифметических выражений, таким образом, что object является многочленным выражением в возвращенных выражениях

При использовании этой опции object рассматривается как многочленное выражение. Неполиномиальные подвыражения, такие как sin(x), x^(1/3), 1/(x+1), или f(a, b), рассматриваются как indeterminates и включены в возвращенный набор. Однако подвыражения, такие как f(2, 3) рассматриваются как константы, даже когда идентификатор f не имеет никакого значения. Философия позади этого - то, что выражение является постоянным, потому что операнды являются постоянными (см. Пример 1).

Если object является массивом, списком, набором или таблицей, то indets возвращает набор арифметических выражений, таким образом, что каждая запись object является многочленным выражением в этих выражениях. Смотрите Пример 2.

RatExpr

Возвратите набор арифметических выражений, таким образом, что object является рациональным выражением в возвращенных выражениях

При использовании этой опции object рассматривается как рациональное выражение. Подобно PolyExpr нерациональные подвыражения рассматриваются как indeterminates (см. Пример 1).

Возвращаемые значения

набор арифметических выражений.

Перегруженный

object

Алгоритмы

Если object является элементом библиотеки domainT, который имеет слот "indets", то стандартная программа слота T::indets вызвана object в качестве аргумента. Это может использоваться, чтобы расширить функциональность indets к пользовательским областям. Если никакой такой слот не существует, то indets возвращает пустое множество.

Смотрите также

Функции MuPAD

Type::Indeterminate | Type::PolyExpr | Type::RatExpr | collect | domtype | op | poly | rationalize | type

Документация