rationalizeПреобразуйте выражение в рациональное выражение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
rationalize(object, options)
rationalize(object) преобразовывает выражение object в эквивалентное рациональное выражение, заменяя нерациональные подвыражения недавно сгенерированными переменными.
По умолчанию рациональное выражение является выражением, которое содержит только суммы, продукты, степени с целочисленными экспонентами, целыми числами, рациональными числами и идентификаторами как подвыражения.
Функция rationalize возвращает последовательность (rat, subsSet). Рационализированное выражение rat содержит новые переменные. Набор замен subsSet выражает новые переменные старыми единицами.
Если исходное выражение содержит подвыражения, функция rationalize может рационализировать или заменить подвыражения или сохранить их в их исходной форме. Используйте опции DescendInto, ReplaceType и StopOn, чтобы управлять мерами, которые rationalize принимает для конкретных типов подвыражений.
Если FindRelations = ["exp", "_power", "sin"], функция rationalize обнаруживает максимальное количество алгебраических зависимостей.
Если вы вызываете rationalize с какой-либо комбинацией следующих трех опций противоречия, функция выбирает опцию с помощью следующих приоритетов: ReplaceType, StopOn, DescendInto. Например, если вы задаете тот же тип подвыражения с StopOn и DescendInto, функция rationalize использует только опцию StopOn для подвыражений заданного типа. Если вы комбинируете какую-либо из этих опций с опцией ReplaceType, rationalize использует только опцию ReplaceType.
rationalize работает с одним арифметическими выражениями, списками и наборами выражений:
rationalize(2*sqrt(3) + 0.5*x^3)
![]()
rationalize([(x - sqrt(2))*(x^2 + sqrt(3)),
(x - sqrt(2))*(x - sqrt(3))])![]()
Используйте опцию ApproximateFloats, чтобы заменить все числа с плавающей запятой на рациональные числа:
rationalize([0.4, 0.333, 0.74], ApproximateFloats)
![]()
Если вы используете и ApproximateFloats и опции ReplaceTypes, ApproximateFloats не применяется к типам подвыражений, заданных в ReplaceTypes:
rationalize(0.4*x^2 + sin(0.33/x),
ApproximateFloats,
ReplaceTypes={DOM_FLOAT})![]()
Вместо того, чтобы задать значение ReplaceTypes как последовательность типов, можно задать его как функцию. Функция должна возвратить TRUE или FALSE в результате. Например, рационализируйте то же выражение![]() . На этот раз используйте функциональный
. На этот раз используйте функциональный F, чтобы задать тип подвыражений, которые вы хотите заменить переменными:
F := X -> testtype(X, DOM_FLOAT):
rationalize(0.4*x^2 + sin(0.33/x),
ApproximateFloats,
ReplaceTypes = F)![]()
По умолчанию rationalize рационализирует суммы, продукты, основы целочисленных степеней, списков и наборов:
rationalize(ln(sin(x)^2 + cos(x)*exp(x)))
![]()
Опция DescendInto позволяет вам задать типы подвыражений, которые вы хотите рационализировать. Каждый тип может быть доменным типом, строка, как возвращено функциональным type или Текстовым объектом. Обратите внимание на то, что DescendInto перезаписывает типы по умолчанию с типами, которые вы задаете:
rationalize(ln(sin(x)^2 + cos(x)*exp(x)), DescendInto = {"ln"})![]()
Если вы хотите добавить новые типы подвыражений к единицам по умолчанию, задать значение DescendInto как процедура, которая задает все необходимые типы явным образом. Процедура должна возвратить TRUE или FALSE:
F := proc(X)
begin
hastype(X, {"_plus", "_mult", DOM_SET, DOM_LIST, "ln"}) or
(hastype(X, "_power") and hastype(op(X, 2), DOM_INT))
end:
rationalize(ln(sin(x)^2 + cos(x)*exp(x)), DescendInto = F)![]()
Используйте опцию MinimalPolynomials, чтобы найти минимальные полиномы иррациональных выражений:
rationalize(x^(7/6) + x^(3/2), MinimalPolynomials)
![]()
Используйте Prefix = s, где s является строкой, чтобы задать префикс для сгенерированных переменных (префиксом по умолчанию является X):
rationalize(x^(7/6) + x^(3/2), Prefix = "ABC")
![]()
Используйте опцию ReplaceHardToEval, чтобы заменить пределы, суммы и интегралы со сгенерированными переменными. Выражения с пределами, суммами и интегралами имеют тенденцию быть наиболее в вычислительном отношении дороги:
rationalize(sum(exp(x)/(x^2 + 1), x) +
limit(sin(cos(1/x))*cos(1/x), x),
ReplaceHardToEval)
По умолчанию rationalize избегает рационализации целых чисел, рациональных чисел и идентификаторов:
rationalize(2*sqrt(3) + 0.5*x^3)
![]()
Опция DescendInto позволяет вам избежать рационализации конкретных типов подвыражений. Каждый тип может быть задан как доменный тип, строка, как возвращено функциональным type или Текстовым объектом. Например, рационализируйте то же выражение, оставив подвыражение x^3 (типа "_power") неизменный:
rationalize(2*sqrt(3) + 0.5*x^3, StopOn = {"_power"})![]()
Рационализируйте то же выражение включая все подвыражения. Сохраните числа с плавающей запятой, целые числа и идентификаторы (не заменяйте их на сгенерированные переменные):
rationalize(2*sqrt(3) + 0.5*x^3,
StopOn = {DOM_FLOAT, DOM_INT, DOM_IDENT})![]()
Обратите внимание на то, что StopOn перезаписывает типы по умолчанию с типами, которые вы задаете. Если вы хотите добавить новые типы подвыражений к единицам по умолчанию, задайте все типы явным образом:
rationalize(2*sqrt(3) + 0.5*x^3,
StopOn = {DOM_INT, DOM_IDENT, DOM_RAT, DOM_FLOAT})![]()
rationalize(2*sqrt(3) + 0.5*x^3,
StopOn = {DOM_INT, DOM_IDENT,
DOM_RAT, DOM_FLOAT,
"_power"})![]()
Опция StopOn также может принять функцию как свое значение. Функция должна возвратить TRUE или FALSE. Например, используйте сгенерированные переменные, чтобы заменить только подвыражения, которые содержат sin. Сохраните все другие подвыражения в целости:
F := X -> not hastype(X, "sin"): rationalize(sin(x^2) + x^3 + exp(x) + 1/x, StopOn = F)
![]()
Используйте опцию FindRelations, чтобы обнаружить алгебраические зависимости между экспоненциалами:
rationalize(exp(x/2) + exp(x/3), FindRelations = ["exp"])
![]()
Обнаружьте алгебраические зависимости для различных степеней той же основы путем определения типа "_power":
rationalize(x^(3/2) + x^(7/4), FindRelations = ["_power"])
![]()
Обнаружьте алгебраические зависимости для тригонометрических функций путем определения типа "sin" или "cos":
rationalize(sin(x) + cos(x), FindRelations = ["sin"]); rationalize(sin(x)^3 + cos(x)^3, FindRelations = ["cos"])

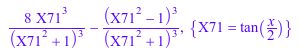
Для вложенных экспоненциалов используйте опцию Recursive, чтобы получить список замен:
rationalize(exp(exp(x)), FindRelations = ["exp"], Recursive)
![]()
Опция также работает на тригонометрические функции:
rationalize(sin(sin(x)), FindRelations = ["sin"], Recursive)
![]()
Опция ShowDependencies показывает все исходные переменные, от которых зависит каждая сгенерированная переменная:
rationalize(sin(x)^3, ShowDependencies)
![]()
|
Любой объект MuPAD® |
|
Когда вы используете опцию |
|
Когда вы используете опцию
По умолчанию функция |
|
Когда вы используете опцию |
|
Когда вы используете опцию |
|
Используйте опцию |
|
Когда вы используете опцию |
|
Когда вы используете опцию |
|
Когда вы используете опцию
Эта опция позволяет вам задавать и избегать большинства дорогих рационализаций для своего конкретного выражения. Если вы используете эту опцию в сочетании с Также задайте значение этой опции как функция, которая возвращает |
|
Когда вы используете опцию |
|
Когда вы используете опцию
По умолчанию функция Если |
|
Когда вы используете опцию |
Последовательность, состоящая из рационализированного объекта и набор уравнений замены. Если вы используете опцию Recursive, функция rationalize возвращает список уравнений замены вместо набора. Если вы используете опцию MinimalPolynomials, возвращенное значение имеет третий аргумент: минимальные полиномы.