collectСоберите условия с теми же степенями
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
collect(p,g, <f>) collect(p,[g1, g2, …], <f>)
Группы collect(p, g) называют с теми же степенями g в выражении p.
Группы collect(p, [g1, g2, ...]) называют с теми же степенями g 1, g 2, … в многомерном выражении p.
Если вы передаете имя функции f в качестве третьего аргумента к collect, процедура собирает степени g (g 1, g 2, … для многомерного выражения). Затем это применяет функциональный f к коэффициентам.
collect(p, g) представляет p как сумму . Коэффициенты a i не являются полиномами в g. Эти коэффициенты могут содержать некоторые условия с g, например, sin (g) или .
collect возвращает измененную копию полинома. Функция не изменяет сам полином. Смотрите Пример 1.
Если p является рациональным выражением в g, collect обрабатывает числитель и знаменатель отдельно.
Если p является многомерным выражением, collect (p, [g 1, g 2, …]) возвращает выражение в следующей форме:
Коэффициенты a i 1, i 2, … не является полиномами в g. Эти коэффициенты могут содержать некоторые условия с g 1, g 2, …, например, .
Если p является рациональным выражением в g 1, g 2, …, команда collect обрабатывает числитель и знаменатель отдельно.
Для многочленных выражений collect внутренне вызывает две функции: poly и затем expr. Функциональный poly преобразовывает выражение p в полином в данных неизвестных. Эта функция возвращает полином с условиями, собранными теми же степенями. Затем expr преобразовывает этот полином в многочленное выражение. Смотрите poly для получения дополнительной информации и примеры. Когда применено рациональное выражение, collect обрабатывает числитель и знаменатель отдельно.
Можно использовать произвольные выражения в качестве indeterminates. Смотрите Пример 2.
Можно задать имя функции вместо переменной. В этом случае collect обрабатывает все вызовы функции с различными аргументами как различные переменные. Смотрите Пример 4.
collect рекурсивно не собирает операнды неполиномиальных подвыражений p. Смотрите Пример 2.
Если p не является многочленным выражением, collect может возвратить неизменное выражение p. Смотрите Пример 5.
Можно задать многочленное выражение p и собрать условия с теми же степенями x и y:
p := x*y + z*x*y + y*x^2 - z*y*x^2 + x + z*x; collect(p, [x, y])
![]()
![]()
collect не изменяет исходное выражение:
p
![]()
Можно собрать условия с теми же степенями x:
collect(p, [x])
![]()
Если выражение содержит только один неопределенный, можно не использовать квадратные скобки во втором аргументе вызова функции:
collect(p, x)
![]()
К факторным коэффициентам в получившемся выражении передайте factor в качестве третьего аргумента к collect:
collect(p, x, factor)
![]()
collect не изменяет неполиномиальные подвыражения, даже если они содержат данное неопределенное. В частности, collect рекурсивно не обрабатывает операнды неполиномиального подвыражения:
collect(sin((x + 1)^2)*(x + 1) + 5*sin((x + 1)^2) + x, x)
![]()
collect принимает неполиномиальные подвыражения как indeterminates:
collect(sin((x + 1)^2)*(x + 1) + 5*sin((x + 1)^2) + x,
sin((x + 1)^2))![]()
collect нормирует рациональное выражение, и затем обрабатывает числитель и знаменатель отдельно:
collect(z/(x+y) + 3*z/(x+z), z)
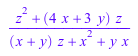
Если вы задаете имя функции как неопределенный, collect вызовы функций указателей с различными аргументами как различный indeterminates:
collect(a*f(1) + c*f(1) + f(2) + d*f(2), f)
![]()
collect(a*sin(x) + b*sin(x) + c*sin(y) + d*sin(y), sin)
![]()
p:= diff(besselJ(0, x), x $ 4); collect(p, besselJ); collect(p, besselJ, expand);
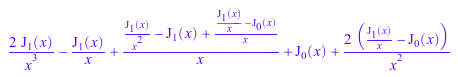
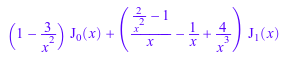
![]()
Если p не является многочленным выражением, collect может возвратить неизменное выражение p:
p := y^2*sin(x) + y*sin(x) + y^2*cos(x) + y*cos(x); collect(p, x)
![]()
![]()
Выражение p является многочленным выражением в y. Можно сгруппировать условия с теми же степенями в этой переменной:
collect(p, y)
![]()
| |
|
indeterminates: обычно, идентификаторы или индексированные идентификаторы. |
|
p