linalg:: gaussJordanИсключение по Гауссу-Жордану
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::gaussJordan(A, <All>)
linalg::gaussJordan(A) выполняет Исключение по Гауссу-Жордану на матричном A, т.е. это возвращает приведенный ступенчатый по строкам вид матрицы A.
Кольцевой R компонента A должен быть интегральной областью, т.е. областью категории Cat::IntegralDomain.
Если R является полем, т.е. областью категории Cat::Field, то ведущие записи матричного T в приведенном ступенчатом по строкам виде матрицы равны одному.
Если R является звонком, предоставляющим метод "gcd", то компоненты каждой строки T не имеют нетривиального общего делителя.
Если звонок компонента A является полем, то приведенный ступенчатый по строкам вид матрицы уникален.
Мы применяем Исключение по Гауссу-Жордану к следующей матрице:
A := Dom::Matrix(Dom::Rational)( [[1, 2, 3, 4], [-5, 0, 3, 0], [3, 5, 6, 9]] )

linalg::gaussJordan(A, All)
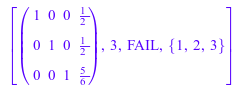
Мы видим что rank (B) = 3. Поскольку детерминант матрицы только задан для квадратных матриц, третий элемент возвращенного списка является значением FAIL.
Если мы рассматриваем матрицу от Примера 1 как целочисленная матрица и применяем Исключение по Гауссу-Жордану, мы получаем следующую матрицу:
B := Dom::Matrix(Dom::Integer)( [[1, 2, 3, 4], [-5, 0, 3, 0], [3, 5, 6, 9]] ): linalg::gaussJordan(B)

|
Матрица области категории |
|
Возвращает список Если |
матрица того же доменного типа как A или список [T, rank(A), det(A), {j_1,dots,j_r}], когда опция All будет дан (см. ниже).
Позвольте T = (t i, j) 1 ≤ i ≤ m, 1 ≤ j ≤ n быть m ×n матрица. Затем T является матрицей в приведенном ступенчатом по строкам виде матрицы, если r ∈ {0, 1, …, n} и индексы j 1, j 2, …, j r ∈ {1, …, n} существует с:
j 1 <j 2 <··· <j r.
Для каждого i ∈ {1, …, r}: t i, 1 = t i, 2 = ··· = t i, j i - 1 = 0. Кроме того, если A задан по полю: t i, j i = 1.
Для каждого i ∈ {r + 1, …, m}: t i, j = 0 для каждого j ∈ {1, …, n}.
Для каждого i ∈ {1, …, r}: t k, j i = 0 для каждого k ∈ {1, …, i - 1}.
Индексы j 1, j 2, …, j r является характеристическими индексами столбца матричного T.