linalg:: matlinsolveLUРешение линейной системы, данной разложением LU
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::matlinsolveLU(L,U,b) linalg::matlinsolveLU(L,U,B)
linalg::matlinsolveLU(L, U, b) решает линейную систему
, где матрицы L и U формируют разложение LU, как вычислено linalg::factorLU.
Если третьим параметром является n ×k матричный B затем, результатом является n ×k матричный X, удовлетворяющий матричному уравнению L U X = B.
Система, которая будет решена всегда, имеет уникальное решение.
Диагональные элементы более низкого диагонального матричного L должны быть равны одному (Doolittle-разложение, смотрите linalg::factorLU).
linalg::matlinsolveLU ожидает, что L и U будут несингулярны.
linalg::matlinsolveLU не проверяет ни одного из необходимых свойств L и U.
Звонок компонента матриц L и U должен быть полем, т.е. областью категории Cat::Field.
Параметры должны быть заданы по тому же звонку компонента.
Мы решаем систему
:
MatR := Dom::Matrix(Dom::Real): A := MatR([[2, -3, -1], [1, 1, -1], [0, 1, -1]]); I3 := MatR::identity(3)
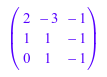
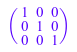
Мы запускаем путем вычисления разложения LU A:
LU := linalg::factorLU(A)
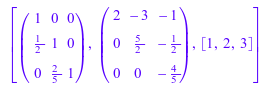
Теперь мы решаем систему A X = I 3, который дает нам инверсию A:
Ai := linalg::matlinsolveLU(LU[1], LU[2], I3)
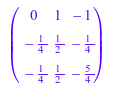
A * Ai, Ai * A
|
n ×n нижняя треугольная матрица области категории |
|
n ×n верхняя треугольная матрица формы той же области как |
|
n ×k матрица области категории |
|
n - размерный вектор-столбец, т.е. n ×1 матрица области категории |
n- вектор решения или n ×k размерная матрица решения, соответственно, доменного типа Dom::Matrix(R), где R является звонком компонента A.