linalg:: factorLUРазложение LU матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::factorLU(A)
linalg::factorLU(A) вычисляет разложение LU m ×n матричный A, т.е. разложение A в m ×m нижний треугольный матричный L и m ×n верхняя треугольная матрица U, таким образом, что P A = L U, где P является матрицей перестановок.
Диагональные элементы нижнего треугольного матричного L равны одному (Doolittle-разложение). Диагональные элементы U являются элементами центра, используемыми во время вычисления.
Матрицы L и U уникальны.
pivindex является списком [ r1, r2, ...], представляющий обмены строки A на вертящихся шагах, т.е. B = P A = L U, где b ij = a r i, j.
Приближение с плавающей точкой разложения вычисляется с помощью numeric::factorLU, если матричный A задан по кольцевому Dom::Float компонента. В этом случае рекомендуется вызвать numeric::factorLU непосредственно для лучшей эффективности.
Алгоритм также работает на сингулярный A. В этом случае или L или U сингулярны.
L и U несингулярны, если и только если A несингулярен.
Звонок компонента матричного A должен быть полем, т.е. областью категории Cat::Field.
Мы вычисляем разложение LU действительной матрицы:
A := Dom::Matrix(Dom::Real)( [[2, -3, -1], [1, 1, -1], [0, 1, -1]] )
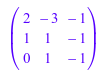
[L, U, pivlist] := linalg::factorLU(A)
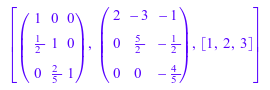
Нижний треугольный матричный L является первым элементом und верхняя треугольная матрица, U является вторым элементом списка LU. Продукт этих двух матриц равен входной матрице A:
L * U
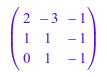
Разложение LU 3×2 матрица:
A := Dom::Matrix(Dom::Real)([[2, -3], [1, 2], [2, 3]])
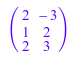
дает 3×3 нижняя треугольная матрица и 3×2 верхняя треугольная матрица:
[L, U, pivlist] := linalg::factorLU(A)
L * U
Вычислить разложение LU матрицы:
A := matrix([[1, 2, -1], [0, 0, 3], [0, 2, -1]])
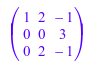
один обмен строки необходим, и мы поэтому получаем нетривиальный список перестановок:
[L, U, pivlist] := linalg::factorLU(A)
Соответствующая матрица перестановок следующая:
P := linalg::swapRow(matrix::identity(3), 3, 2)
Следовательно, у нас есть разложение A в продукт этих трех матриц
, L и U можно следующим образом:
P^(-1) * L * U
Можно вычислить разложение LU матрицы с символьными компонентами, такими как:
delete a, b, c, d: A := matrix([[a, b], [c, d]])
Диагональные элементы матричного U являются элементами центра, используемыми во время вычисления. Они должны быть ненулевыми, если инверсия U необходима:
[L, U, pivlist] := linalg::factorLU(A)
Например, если мы используем это разложение, чтобы решить линейную систему
для произвольных векторов
, затем следующий результат только правилен для a ≠ 0 и
:
delete b1, b2: linalg::matlinsolveLU(L, U, matrix([b1, b2]))
|
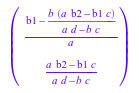
Матрица области категории |
Перечислите [L, U, pivindex] с этими двумя матрицами L и U доменного Dom::Matrix (R) и список pivindex положительных целых чисел. R является звонком компонента A.
Следующий алгоритм для решения системы
с несингулярным матричным A использует разложение LU:
Вычислите разложение LU A: A = L U.
Решите
прямой заменой.
Решите
обратной подстановкой.
Разложение LU матричного A полезно для решения нескольких систем линейных уравнений
с той же матрицей коэффициентов A и несколько правых векторов стороны
, потому что затем продвигаются, один из алгоритма выше должен быть сделан только однажды.