linalg:: pascalМатрица Паскаля
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
linalg::pascal(n, <R>)
linalg::pascal(n) возвращает n ×n матрица Паскаля P, данный
, 1 ≤ i, j ≤ n.
Записи матриц Паскаля являются целыми числами. Обратите внимание, однако, что возвращенная матрица не задана по доменному Dom::Integer компонента, но по стандартному доменному Dom::ExpressionField() компонента. Таким образом никакое преобразование не необходимо при работе с другими функциями, которые ожидают или возвращают матрицы по той области компонента.
Используйте linalg::pascal(n, Dom::Integer), чтобы задать n ×n матрица Паскаля по звонку целых чисел.
Обратные матрицы Паскаля предоставлены linalg::invpascal.
Мы создаем 3×3 матрица Паскаля:
linalg::pascal(3)
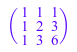
Это - матрица доменного Dom::Matrix().
Если вы предпочитаете различный звонок компонента, матрица может быть преобразована в желаемую область после конструкции (см. coerce, например). Также можно задать звонок компонента при создании матрицы Паскаля. Например, спецификация доменного Dom::Float генерирует записи с плавающей точкой:
linalg::pascal(3, Dom::Float)
domtype(%)
Фактор Холесского матрицы Паскаля состоит из элементов треугольника Паскаля:
linalg::factorCholesky(linalg::pascal(4))
|
Размерность матрицы: положительное целое число |
|
Звонок компонента: область категории |
n ×n матрица доменного Dom::Matrix (R).
Матрицы Паскаля симметричны и положительные определенный.
Детерминант матрицы Паскаля равняется 1.
Инверсия матрицы Паскаля имеет целочисленные записи.
Если λ является собственным значением матрицы Паскаля, то
является также собственным значением матрицы.