числовой::Факторизация Холесского матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::factorCholesky(A, options)
numeric::factorCholesky(A) возвращает факторный L факторизации Холесского A = L LH положительной определенной Эрмитовой матрицы A.
numeric::factorCholesky(A, Symmetric) возвращает факторный L факторизации типа Холесского A = L LT симметрической матрицы A.
Факторизацией Холесского квадратной Эрмитовой матрицы является A = L LH, где L является регулярной комплексной нижней треугольной матрицей и L, H является Эрмитовым, транспонируют L (т.е. сопряженное комплексное число транспонирования L). Такая факторизация только существует, если A положителен определенный.
По умолчанию числовая факторизация вычисляется. Если опция, Symbolic не используется, все компоненты матрицы, преобразована в числа с плавающей запятой. В этом случае матрица не должна содержать символьные объекты, которые не могут быть преобразованы в плавания. Числовые символьные выражения, такие как π![]() ,
, ![]() и т.д. приняты.
и т.д. приняты.
Если никакие не возвращаются, тип задан с помощью опции ReturnType = d, доменный тип Фактора Холесского, L зависит от типа входной матрицы A:
Фактором плотной матрицы типа Dom::DenseMatrix() является плотная матрица типа Dom::DenseMatrix() по звонку выражений MuPAD®.
Для всех других матриц категории Cat::Matrix факторный L возвращен как matrix типа Dom::Matrix() по звонку выражений MuPAD. Это включает входные матрицы A типа Dom::Matrix(...), Dom::SquareMatrix(...), Dom::MatrixGroup(...) и т.д.
Фактор Холесского, возвращенный numeric::factorCholesky, нормирован таким образом, что его диагональные элементы действительны и положительны.
Без опции Symbolic функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы рассматриваем матрицу
A := array(1..2, 1..2, [[1, I] , [-I, PI]]):
Мы вычисляем числовую факторизацию
numeric::factorCholesky(A)
![]()
и символьная факторизация:
L := numeric::factorCholesky(A, Symbolic)
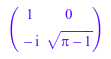
Для последующей обработки Фактор Холесского (доменного типа DOM_ARRAY) преобразован в элемент матричного доменного Dom::Matrix ():
L := matrix(L):
Теперь, перегруженные арифметические операторы +, *, ^ и т.д. может использоваться для дальнейших вычислений:
L*linalg::transpose(conjugate(L))
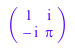
delete A, L:
Следующая матрица не положительна определенный:
A := matrix([[-2, sqrt(2)], [sqrt(2), 1]]): numeric::factorCholesky(A)
Error: Matrix not positive definite within working precision. [stdlib::hfa::factorCh] Evaluating: numeric::factorCholesky
Однако симметричная факторизация с комплексным Фактором Холесского действительно существует:
numeric::factorCholesky(A, Symmetric)

delete A:
NoCheck опции должен использоваться, когда матрица содержит символьные объекты:
assume(x > 0): assume(z > 0): A := array(1..2, 1..2, [[x, conjugate(y)], [y, z]]): numeric::factorCholesky(A, Symbolic, NoCheck)
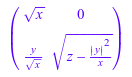
Обратите внимание на то, что с NoCheck, это принято, что матрица Эрмитова и положительная определенный! Проигнорированы все верхние треугольные записи. Следующий результат неявно принимает u = conjugate(y):
A := array(1..2, 1..2, [[x, u], [y, z]]): numeric::factorCholesky(A, Symbolic, NoCheck)
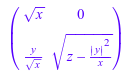
delete A:
Мы демонстрируем использование аппаратных плаваний. Гильбертовы матрицы являются известно плохо обусловленными и трудными к фактору с низкими значениями DIGITS. Следующие результаты, оба с HardwareFloats, а также с SoftwareFloats, омрачены числовым округлением. Следовательно, факторизация с и без аппаратных плаваний, соответственно, значительно отличается:
A := linalg::hilbert(13): L1 := numeric::factorCholesky(A, HardwareFloats): L2 := numeric::factorCholesky(A, SoftwareFloats): L1[13, 13] <> L2[13, 13]
![]()
Все Гильбертовы матрицы положительны определенный. Однако в следующем вызове, числовое округление делает оборудование инструмент, с плавающей точкой думает, что матрица не является определенной:
numeric::factorCholesky(linalg::hilbert(14), HardwareFloats):
Error: Matrix not positive definite within working precision. [stdlib::hfa::factorCh] Evaluating: numeric::factorCholesky
Факторизация вычисляется успешно с SoftwareFloats:
L := numeric::factorCholesky(linalg::hilbert(14), SoftwareFloats): norm(linalg::hilbert(14) - L*linalg::transpose(L))
![]()
delete A, L1, L2, L:
|
Квадратная матрица доменный тип |
|
С С По сравнению с Если никакой Если результат не может быть вычислен с аппаратными плаваниями, арифметику программного обеспечения ядром MuPAD пробуют. Если текущее значение Может быть несколько причин аппаратной арифметики, чтобы перестать работать:
Если ни Если Обратите внимание на то, что Запаздывающие цифры в результатах с плавающей точкой, вычисленных с ПримечаниеДля плохих обусловленных матриц результаты, возвращенные с |
|
Предотвращает преобразование входных данных к числам с плавающей запятой. Точная арифметика используется. Эта опция заменяет Обычная арифметика для выражений MuPAD используется. При использовании этой опции матричный A может содержать символьные объекты. Обратите внимание на то, что |
|
Заставляет Симметричной факторизацией Холесского квадратной симметрической матрицы является A = L LT, где L является регулярной комплексной нижней треугольной матрицей и L, T является транспонированием L. Матричный A не должен быть положителен определенный. Следовательно, с опцией Для действительных симметричных положительных определенных матриц A Фактор Холесского L действителен и Эрмитова факторизация A = L, LH совпадает с симметричной факторизацией A = L LT. |
|
Препятствует тому Без опции ПримечаниеПри использовании этой опции Эта опция не имеет никакого эффекта, когда опция |
|
Отключает предупреждения Если символьные коэффициенты найдены, |
|
Опция, заданная как Возвратите Фактор Холесского как матрицу доменного типа |
В зависимости от типа входной матрицы A нижний треугольный Фактор Холесского L возвращен как матрица доменного типа DOM_ARRAY, DOM_HFARRAY, Dom::Matrix() или Dom::DenseMatrix(). Его компоненты являются действительными или комплексными плаваниями, если опция Symbolic не используется. Без опции NoCheck повышена ошибка, если матрица не Эрмитова или не положительная определенный.