числовой::LU-факторизация матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::factorLU(A, options)
numeric::factorLU(A) возвращает факторизацию LU матричного A.
Факторизацией LU действительного или комплексного m ×n матричный A является P A = L U. m ×m матричный L является нижним треугольным, нормирован к 1 по диагонали. m ×n матричный U верхний треугольный, т.е. U ij = 0 для j <i. Список p = [p1, …, pm], возвращенный numeric::factorLU, является перестановкой чисел 1, …, m, соответствующий обменам строки A. Это представляет следующий m ×m матрица перестановок P (мы принимаем, что матричные индексы колеблются от 1 до m):
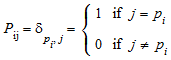 .
.
Оставленное умножение матриц и векторов с P понято легко с помощью списка перестановки p: Y i, j: = X p i, j задает перестановку строки Y = P X матричного X, y i: = x p i задает перестановку строки y = P x векторного x.
По умолчанию числовая факторизация с частичным поворотом вычисляется. Если опция, Symbolic не используется, все компоненты матрицы, преобразована в числа с плавающей запятой. В этом случае матрица не должна содержать символьные объекты, которые не могут быть преобразованы в плавания. Числовые символьные выражения, такие как π![]() ,
, ![]() и т.д. приняты.
и т.д. приняты.
Факторизация зависит от вертящейся стратегии. Результаты, полученные с/без опцией Symbolic, могут отличаться. Смотрите Пример 2. Для числовых факторизаций могут отличаться результаты, полученные с HardwareFloats и SoftwareFloats, соответственно. Смотрите Пример 3.
Если никакие не возвращаются, тип задан с помощью опции ReturnType = d, доменный тип факторов, L и U зависят от типа входной матрицы A:
Факторами плотной матрицы типа Dom::DenseMatrix() являются снова плотные матрицы типа Dom::DenseMatrix() по звонку выражений MuPAD®.
Для всех других матриц категории Cat::Matrix факторы возвращены как матрицы типа Dom::Matrix() по звонку выражений MuPAD. Это включает входные матрицы A типа Dom::Matrix(...), Dom::SquareMatrix(...), Dom::MatrixGroup(...) и т.д.
Без дополнительного аргумента Symbolic функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы учитываем матрицу, заданную массивом:
A := array(1..3, 1..3, [[1, 2, 3], [2, 4, 6], [4, 8, 9]]): [L, U, p] := numeric::factorLU(A)

Факторы (доменного типа DOM_ARRAY) преобразованы в элементы матричного доменного Dom::Matrix (). После преобразования, перегруженные арифметические операторы +, *, ^ и т.д. может использоваться для последующей обработки:
L := matrix(L): U := matrix(U): L*U

Продукт L U совпадает с A после обмена строками согласно перестановке, сохраненной в списке p:
PA := array(1..3, 1..3, [[A[p[i], j] $ j=1..3] $ i=1..3])

delete A, L, U, p, PA:
Мы считаем неквадратную матрицу размерности 3 ×2:
A := matrix([[3*I, 10], [I, 1], [I, 1]]): [L1, U1, p1] := numeric::factorLU(A)
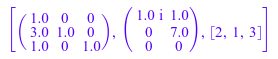
Обратите внимание на то, что символьная факторизация отличается, потому что используется различная вертящаяся стратегия:
[L2, U2, p2] := numeric::factorLU(A, Symbolic)
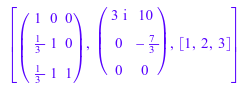
Здесь, матричные факторы имеют тип Dom::Matrix(), потому что входная матрица A имела этот тип. Мы можем использовать перегруженную арифметику непосредственно. Мы преобразовываем списки перестановок p1, p2 к матрицам и проверяем отношение P A = L U для факторизации:
P1 := matrix(3, 3): P2 := matrix(3, 3): for i from 1 to 3 do P1[i, p1[i]] := 1; P2[i, p2[i]] := 1; end_for: P1*A - L1*U1, P2*A - L2*U2
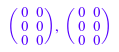
delete A, L1, U1, p1, L2, U2, p2:
Мы демонстрируем использование аппаратных плаваний. Внутреннее округление HardwareFloats и SoftwareFloats отличается. Следовательно, следующие результаты не совпадают:
n := 14: A := linalg::hilbert(n): [L1, U1, p1] := numeric::factorLU(A, HardwareFloats): [L2, U2, p2] := numeric::factorLU(A, SoftwareFloats): p1, p2
![]()
Однако обе факторизации удовлетворяют P A = L U численно:
P1A := matrix([[A[p1[i], j] $ j = 1..n] $ i = 1..n]): P2A := matrix([[A[p2[i], j] $ j = 1..n] $ i = 1..n]): norm(P1A - L1*U1), norm(P2A - L2*U2)
![]()
delete n, A, L1, U1, p1, L2, U2, p2, P1A, P2A:
|
m ×n матрица доменный тип |
|
С С По сравнению с Если никакой Если результат не может быть вычислен с аппаратными плаваниями, арифметику программного обеспечения ядром MuPAD пробуют. Если текущее значение Может быть несколько причин аппаратной арифметики, чтобы перестать работать:
Если ни Если Обратите внимание на то, что Запаздывающие цифры в результатах с плавающей точкой, вычисленных с ПримечаниеДля плохих обусловленных матриц результаты, возвращенные с |
|
Предотвращает преобразование входных данных к числам с плавающей запятой. Точная арифметика используется. Эта опция заменяет Обычная арифметика для выражений MuPAD используется. При использовании этой опции матричный A может содержать символьные объекты. При использовании этой опции никакие обмены строки не выполняются во внутреннем Исключении Гаусса, если не необходимо. |
|
Отключает предупреждения Если символьные коэффициенты найдены, |
|
Опция, заданная как Возвратите факторы как матрицы доменного типа |
Список [L, U, p] возвращен. Доменный тип m ×m матричный L и m ×n матричный U зависит от типа входной матрицы A; p является списком с элементами m, состоящими из перестановки целых чисел 1, …, m. Это представляет обмены строки на вертящихся шагах. Компоненты L и U являются действительными или комплексными плаваниями, если опция Symbolic не используется.