числовой::Преобразуйте систему оды в vectorfield обозначение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
numeric::ode2vectorfield(IVP, fields)
numeric::ode2vectorfield преобразовывает систему обыкновенных дифференциальных уравнений произвольного порядка к векторному полевому представлению, подходящему для числового решателя ОДУ numeric::odesolve2.
numeric::ode2vectorfield является служебной функцией, чтобы сгенерировать входные параметры для числового решателя ОДУ numeric::odesolve2. Этот решатель требует процедуры, представляющей vectorfield f (t, Y) системы первого порядка дифференциальных уравнений (динамическая система)
и исходные данные Y 0 = Y (t 0). Учитывая задачу с начальными значениями IVP, состоящий из (возможно высший порядок) дифференциальные выражения вместе с начальными условиями, numeric::ode2vectorfield преобразовывает уравнения высшего порядка в эквивалентную систему ОДУ первого порядка и возвращает входные параметры для numeric::odesolve2.
Дифференциальные уравнения высшего порядка могут всегда представляться как эквивалентная динамическая система
с некоторым векторным Y. Например, n-th заказывает уравнение
может быть записан как система первого порядка
для вектора
.
Список входов fields correponds к векторному Y. Это должна быть полная спецификация всех функций и их производных через, но не включая самые высокие производные неизвестных функций. Например, для дифференциального уравнения второго порядка 
соответствующий список неизвестных полей
. Дифференциальные уравнения
имеют второй порядок в y и первого порядка в z. Следовательно, соответствующим списком неизвестных полей является [y(t), y'(t), z(t)].
Упорядоченное расположение полей в list определяет упорядоченное расположение компонентов списка, чтобы числовой решатель производит как вектор решения. Cf. Пример 2.
Дифференциальные уравнения должны быть линейными в самых высоких производных неизвестных включенных функций. Например, ОДУ
не допускают. Однако уравнения те, которые
приняты и преобразованы в
.
Полная спецификация начальных условий должна содержаться в IVP: для каждого компонента в list должно быть обеспечено начальное значение. Начальные условия могут быть заданы линейными уравнениями, которые будут решены для начальных значений неизвестных полей автоматически. Например, для fields = [y(t), y'(t), z(t)] начальные условия могут быть заданы явным образом y(t0) = 1, y'(t_0) = 2, z(t0) = 3, скажем, или через линейные уравнения, такие как y(t_0) + z(t_0) = y'(t_0), y(t0) = z(t0), z(t0) = 2 y(t0). Cf. Пример 3.
Дифференциальные уравнения, начальное 'время' t0 и начальные условия могут включить символьные параметры. Однако такие параметры должны оценить к числовым объектам, когда последовательность, возвращенная numeric::ode2vectorfield, передается числовому решателю.
vectorfield процедура f и начальные значения Y0, возвращенный numeric::ode2vectorfield, может также использоваться функциями numeric::odesolve, plot::Ode2d, plot::Ode3d. Cf. Пример 3.
numeric::ode2vectorfield и numeric::odeToVectorField эквивалентны.
Мы рассматриваем задачу с начальными значениями
.
Решатель numeric::odesolve2 требует процедуры f:
для 1-мерного векторного Y = [y (t)] заданный fields. Служебный numeric::ode2vectorfield принимает более удобное представление через арифметические выражения:
IVP := {y'(t) = t*sin(y(t)), y(t0) = y0}:
fields := [y(t)]:
IVP := numeric::ode2vectorfield(IVP, fields)
Эта последовательность может быть передана числовому решателю, который возвращает процедуру, представляющую числовое решение:
t0 := 0: y0 := 1: Y := numeric::odesolve2(IVP)
При вызове числового решения Y вызывает численное интегрирование с начального 'времени' t 0 = 0 ко 'времени', заданному в вызове Y:
Y(0), Y(1), Y(2), Y(3)
delete IVP, fields, Y:
Мы рассматриваем задачу с начальными значениями второго порядка
.
Соответствующее vectorfield представление включает вектор
, заданный fields:
IVP := {y''(t) = t*sin(y(t)), y(0) = 1, y'(0) = 0}:
fields := [y(t), y'(t)]:
numeric::ode2vectorfield(IVP, fields)
Эта последовательность принята numeric::odesolve2. Числовое решение Y возвращает списки, представляющие компоненты вектора, заданного fields:
Y := numeric::odesolve2(%): Y(5)
С переупорядочением неизвестных полей числовой решатель возвращает вектор решения с перестроенными компонентами:
fields := [y'(t), y(t)]: Y := numeric::odesolve2(numeric::ode2vectorfield(IVP, fields)): Y(5)
delete IVP, fields, Y:
Следующий IVP включает неизвестные поля u (t), v (t), w (t). Поскольку это имеет второй порядок в u, первого порядка в v и третьего порядка в w, списке неизвестных, [y(t), y'(t), v(t), w(t), w'(t), w''(t)] является соответствующим:
IVP := {u''(t) - u(t)*v'(t) = exp(-t)*v'(t), v'(t) = w''(t),
u'(t)*w'''(t) = t + u''(t),
u(PI) = 3, u'(PI) = 1,
v(PI) = 0,
w(PI) = w'(PI), w'(PI) = 2 - w(PI), w''(PI) = 3*w(PI)}:
fields := [u(t), u'(t), v(t), w(t), w'(t), w''(t)]:
ivp := numeric::ode2vectorfield(IVP, fields)
Y := numeric::odesolve2(ivp): Y(5)
Мы строим компоненты v, w, и
вектора решения:
plotfunc2d(Y(t)[3], Y(t)[4], Y(t)[6], t = PI .. 5,
Colors = [RGB::Red, RGB::Green, RGB::Blue]):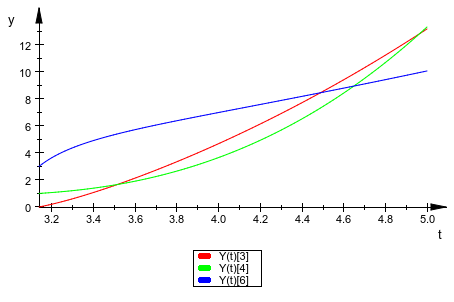
Также мы используем vectorfield процедуру ivp[1] и начальные условия ivp[3] как входные параметры для plot::Ode2d:
plot(plot::Ode2d([PI + i*(5 - PI)/30 $ i = 0..30],
ivp[1], ivp[3],
[(t, Y) -> [t, Y[3]], Color = RGB::Red],
[(t, Y) -> [t, Y[4]], Color = RGB::Green],
[(t, Y) -> [t, Y[6]], Color = RGB::Blue])):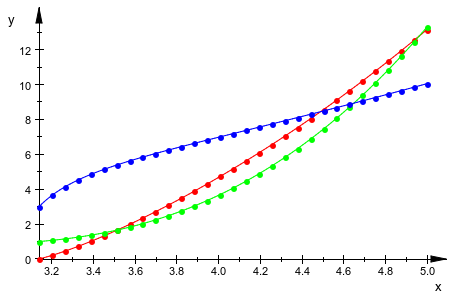
delete IVP, fields, ivp, Y:
|
Задача с начальными значениями: список или набор уравнений, включающих одномерные вызовы функции y 1 (t), y 2 (t) и т.д. и производные |
|
Вектор динамической системы, эквивалентной |
Последовательность f, t0, Y0. Эти данные представляют динамическую систему
с начальным условием Y (t 0) = Y 0, эквивалентный IVP. vectorfield f:
является процедурой, t0 является числовым выражением, представляющим начальное 'время', и Y0 является списком числовых выражений, представляющих компоненты начального векторного Y 0.
, 
, 
, 