график::2D графики решений для ОДУ
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
plot::Ode2d(f,[t0, t1,...],Y0, <[G1, <Style = style1>, <Color = c1>], [G2, <Style = style2>, <Color = c2>], …>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = amin .. amax>,options) plot::Ode2d(f,[Automatic, tstart, tend, tstep],Y0, <[G1, <Style = style1>, <Color = c1>], [G2, <Style = style2>, <Color = c2>],...>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = amin .. amax>,options) plot::Ode2d([t0, t1, …],f,Y0, <[G1, <Style = style1>, <Color = c1>], [G2, <Style = style2>, <Color = c2>],...>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = amin .. amax>,options) plot::Ode2d([Automatic, tstart, tend, tstep],f,Y0, <[G1, <Style = style1>, <Color = c1>], [G2, <Style = style2>, <Color = c2>],...>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = amin .. amax>,options)
plot::Ode2d(f, [t0, t1,...], Y0) представляет двумерные проекции решений задачи с начальными значениями, данной f, t0 и Y0.
plot::Ode2d(f, [t0, t1,...], Y0, [G]) вычисляет mesh числовых точек выборки Y (t 0), Y (t 1), … представление решения Y (t) дифференциального уравнения первого порядка (динамическая система)
.
Процедура
карты эти точки решения (t i, Y (t i)) в ℝ ×ℂn к сетке 2D точек графика [x i, y i]. Эти точки могут быть соединены прямыми линиями или интерполирующими сплайнами.
Внутренне, последовательность числовых точек выборки
Y_1 := numeric::odesolve(f, t_0..t_1, Y_0, Options),
Y_2 := numeric::odesolve(f, t_1..t_2, Y_1, Options), и так далее
вычисляется, где Options является некоторой комбинацией method, RelativeError = rtol, AbsoluteError = atol и Stepsize = h. Смотрите numeric::odesolve для получения дополнительной информации о векторной полевой процедуре f, начальное условие Y0 и опции.
Служебная функция numeric::ode2vectorfield может использоваться, чтобы произвести входные параметры f, t0, Y0 из набора дифференциальных выражений, представляющих ОДУ. Смотрите Пример 1.
Каждый из “генераторов данных о графике” G1, G2 и т.д. создает графическую кривую решения из числовых точек выборки Y0, Y1, и так далее. Каждый генератор G внутренне называется в форме G(t0, Y0), G(t1, Y1),..., чтобы произвести последовательность точек графика в 2D.
Решатель numeric::odesolve возвращает решение, указывает Y0, Y1, и так далее, как списки или одномерные массивы (фактический тип определяется начальным значением Y0). Следовательно, каждый генератор G должен принять два аргумента (t, Y): t является действительным параметром, Y является “вектором” (или список или 1-мерный массив).
Каждый генератор должен возвратить список с 2 элементами, представляющими (x, y), координаты графической точки, сопоставленной с решением, указывают (t, Y) ОДУ. Все генераторы должны произвести графические данные той же размерности, то есть, 2D данные как списки с 2 элементами для plot::Ode2d. Вот некоторые примеры:
G := (t, Y) -> [t, Y_1] создает 2D график первого компонента вектора решения вдоль y - оси, построенной против переменной t времени вдоль x - ось
G := (t, Y) -> [Y_1, Y_2] создает 2D график фазы, строя первый компонент решения вдоль x - оси и второго компонента вдоль y - ось. Результатом является кривая решения в фазовом пространстве (параметризованный временем t).
Если никакие генераторы не даны, plot::Ode2d графиками по умолчанию все компоненты решения как функции времени, с помощью [Splines, Points] в качестве стиля.
Обратите внимание на то, что произвольные значения, сопоставленные с кривой решения, могут быть отображены графически соответствующим генератором G. Смотрите Пример 2.
Несколько генераторов G1, G2, и так далее может быть задан, чтобы сгенерировать несколько кривых, сопоставленных с той же числовой mesh Y0, Y1, …. Смотрите Пример 1, Пример 2 и Пример 3.
Графические данные, произведенные каждым из генераторов G1, G2,..., состоят из последовательности точек mesh в 2D.
С Style = Points графические данные отображены как дискретный набор точек.
С Style = Lines точки графических данных отображены как кривая, состоящая из сегментов прямой линии между точками выборки. Сами точки не отображены.
С Style = Splines точки графических данных отображены как сглаженная сплайновая кривая, соединяющая точки выборки. Сами точки не отображены.
С Style = [Splines, Points] и Style = [Lines, Points], эффекты используемых стилей объединены, то есть, и точки оценки и прямые линии, или сплайны, соответственно, отображены.
Атрибуты графика, принятые plot::Ode2d, включают Submesh = n, где n является некоторым положительным целым числом. Этот атрибут только имеет эффект на кривые, которые возвращены для графических генераторов с Style = Splines и Style = [Splines, Points], соответственно. Это служит для сглаживания графической сплайновой кривой с помощью достаточно высокого количества точек графика.
n является количеством точек графика между двумя последовательными числовыми точками, соответствующими mesh времени. Значение по умолчанию является n = 4, то есть, сплайны построены как пять сегментов прямой линии, соединяющих числовые точки выборки.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AbsoluteError | максимальная абсолютная ошибка дискретизации | |
AffectViewingBox | влияние объектов на ViewingBox сцены | TRUE |
AntiAliased | сглаженные строки и точки? | TRUE |
Colors | список цветов, чтобы использовать | [RGB::Blue, RGB::Red, RGB::Green, RGB::MuPADGold, RGB::Orange, RGB::Cyan, RGB::Magenta, RGB::LimeGreen, RGB::CadmiumYellowLight, RGB::AlizarinCrimson, RGB::Aqua, RGB::Lavender, RGB::SeaGreen, RGB::AureolineYellow, RGB::Banana, RGB::Beige, RGB::YellowGreen, RGB::Wheat, RGB::IndianRed, RGB::Black] |
Frames | количество кадров в анимации | 50 |
Function | выражение function или процедура | |
InitialConditions | начальные условия ОДУ | |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineWidth | ширина строк | 0.35 |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость строк | TRUE |
Name | имя объекта графика (для браузера и легенды) | |
ODEMethod | числовая схема, используемая для того, чтобы решить ОДУ | DOPRI78 |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | TRUE |
Projectors | спроектируйте решение для ОДУ графических точек | |
RelativeError | максимальная относительная ошибка дискретизации | |
Stepsize | установите постоянный размер шага | |
Submesh | плотность подmesh (дополнительные точки выборки) | 4 |
TimeEnd | время окончания анимации | 10.0 |
TimeMesh | числовая mesh времени | |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 .. 10.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11] |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
USubmesh | плотность дополнительных точек выборки для параметра “u” | 4 |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Следующая процедура f вместе с начальным значением Y0 представляет задачу с начальными значениями
, Y (0) = 2. В MuPAD® одномерный векторный Y представлен списком с одним элементом. Тело функционального f ниже обращается к первому (и только) запись этого списка как Y1 и возвращает одномерный векторный t Y - Y 2 как список с одним элементом. Также начальное условие Y0 является одномерным вектором, представленным списком. Для получения дополнительной информации на формате f, смотрите numeric::odesolve:
f := (t, Y) -> [t*Y[1] - Y[1]^2]: Y0 := [2]:
Также служебная функция numeric::ode2vectorfield может использоваться, чтобы сгенерировать входные параметры более интуитивным способом:
[f, t0, Y0] := [numeric::ode2vectorfield(
{y'(t) = t*y(t) - y(t)^2, y(0) = 2}, [y(t)])]
Числовое решение состоит в том, чтобы состоять из точек выборки по mesh времени t i = i, i = 0, 1, …, 10. Мы используем генератор по умолчанию plot::Ode2d. Это генерирует точки выборки вместе со сглаженной сплайновой кривой, соединяющей эти точки:
p := plot::Ode2d(f, [$ 0..10], Y0,
PointSize = 2*unit::mm,
PointStyle = Stars):Наконец, решение для оды представляется вызовом plot:
plot(p, TicksDistance = 2.0, GridVisible = TRUE,
SubgridVisible = TRUE):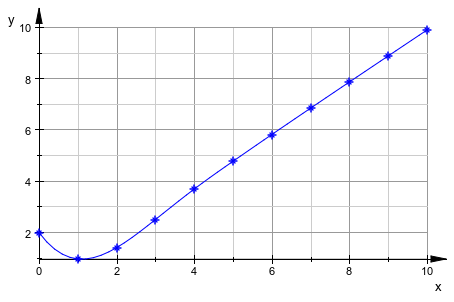
Рассмотрите нелинейный осциллятор
. Как динамическая система для
, решите следующую задачу с начальными значениями
, Y (0) = Y 0. Для получения дополнительной информации на формате f, смотрите numeric::odesolve:
f := (t, Y) -> [Y[2], - Y[1]^7]: Y0 := [1, 0]:
Следующий генератор производит график решения Y (t) против параметра времени t:
G1 := (t, Y) -> [t, Y[1]]:
В демонстрационных целях постройте функцию
. Генератор G2 производит значения
вдоль решения и строит эти значения против t:
G2 := (t, Y) -> [t, Y[1]^2/2 + Y[2]^2/2]:
Энергетическая функция или “гамильтониан”,
должна быть сохранена вдоль кривой решения, потому что полная энергия системы является постоянной. Задайте соответствующий генератор G3, чтобы построить
как функция t:
G3 := (t, Y) -> [t, Y[1]^8/8 + Y[2]^2/2]:
Кривая решения объединена с графиком функции и гамильтониана:
p := plot::Ode2d(f, [i/2 $ i = 0..40], Y0,
[G1, Style = Lines, Color = RGB::Red],
[G1, Style = Points, Color = RGB::Black],
[G2, Style = Lines, Color = RGB::Blue],
[G2, Style = Points, Color = RGB::Black],
[G3, Style = Lines, Color = RGB::Green],
[G3, Style = Points, Color = RGB::Black],
PointSize = 1.5*unit::mm,
LineWidth = 0.2*unit::mm
):Обратите внимание на то, что при помощи каждого генератора дважды, можно выбрать различные цвета для строк и точек. Средство отображения называется:
plot(p):
Гамильтонов G3 является постоянным, который проверяет точность интегратора.
Чтобы визуализировать зависимость траектории на начальных условиях, анимируйте plot::Ode2d по различным значениям
:
plot(plot::Ode2d(f, [i/6 $ i = 0..120], [1, a], a = -1/2..1/2,
[G1, Style = Lines, Color = RGB::Red],
[G2, Style = Lines, Color = RGB::Blue],
[G3, Style = Lines, Color = RGB::Green],
LineWidth = 0.2*unit::mm, Frames=25))
Рассмотрите задачу с начальными значениями
, y (0) = 0:
f := (t, y) -> t*sin(t + y^2): Y0:= [0]:
Используйте numeric::ode2vectorfield, чтобы сгенерировать следующее векторное поле, которое является касательной к кривым решения:
p1 := plot::VectorField2d([1, f(t, y)], t = 0..4, y = -1.2..1.2,
Mesh = [21, 25], Color = RGB::Black):Следующий объект представляет график решения как функция t:
p2 := plot::Ode2d( (t,Y) -> [f(t, Y[1])], [i/3 $ i=0..12], Y0, [(t, Y) -> [t, Y[1]], Style = Points, Color = RGB::Red], [(t, Y) -> [t, Y[1]], Style = Splines, Color = RGB::Blue]):
Задайте размер точки явным образом:
p2::PointSize := 2*unit::mm:
Наконец, объедините векторное поле и график ОДУ к сцене и вызовите средство отображения:
plot(p1, p2, XTicksDistance = 0.5, YTicksDistance = 0.2,
Axes = Frame, AxesTitles = ["t", "y"],
GridVisible = TRUE):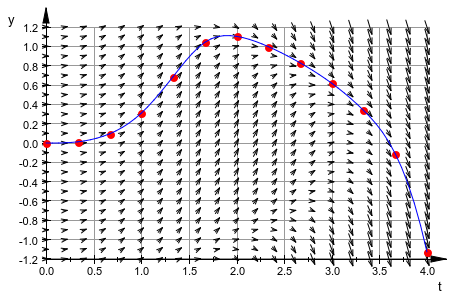
По умолчанию numeric::odesolve (который используется plot::Ode2d внутренне) использует адаптивные размеры шага и метод порядка 8. Обычно, нет никакой причины изменить эти настройки, за исключением демонстративных целей. В следующей анимации используйте прямой явный Метод Эйлера (первого порядка) и покажите, как уменьшение размера шага улучшает качество расчетного решения.
Дифференциальное уравнение
, очевидно, выполнено показательной функцией:
[f, t0, Y0] := [numeric::ode2vectorfield(
{y'(t)=y(t), y(0)=1}, [y(t)])]:Чтобы судить качество числового решения, постройте символьное решение вместе с приближением:
plot(plot::Function2d(exp(x), x=0..3,
Color = RGB::Black, LineStyle = Dashed),
plot::Ode2d(f, [Automatic, 0, 3, 1/n], Y0, n = 1..50,
EULER1, Stepsize = 1/n,
[(t, Y) -> [t, Y[1]], Style=[Lines, Points]]))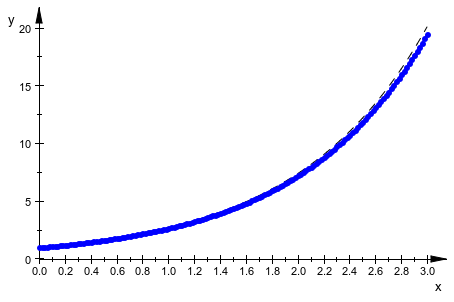
|
Векторное поле ОДУ: процедура. Смотрите
|
|
Mesh времени: действительные численные значения. Если данные отображены с
|
|
Mesh времени: действительные численные значения.
|
|
Начальное условие ОДУ: список или 1-мерный массив. Смотрите
|
|
“генераторы отображают данные на графике”: процедуры, сопоставляющие решение, указывают
|
|
Используйте определенную числовую схему (см. |
|
Параметр анимации, заданный как |
|
Опция, заданная как Устанавливает стиль, в котором отображены данные о графике. Следующие стили доступны: |
|
Опция, заданная как Выбирает цвет RGB |
|
Опция, заданная как Устанавливает числовой допуск дискретизации (см. |
|
Опция, заданная как Устанавливает числовой допуск дискретизации (см. |
|
Опция, заданная как Устанавливает постоянный stepsize (см. |