Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Существует два метода, чтобы получить числовые приближения решений:
Решите уравнения символически и аппроксимируйте полученные символьные результаты численно. Используя этот метод, вы получаете числовые приближения всех решений, найденных символьным решателем. Если символьному решателю не удается найти какие-либо решения, MuPAD® вызывает числовой решатель непосредственно. Для неполиномиальных уравнений числовой решатель возвращает только одно решение. Используя символьный решатель и последующую обработку его метод результатов требует большего количества времени, чем чисто числовой решатель и может значительно уменьшить производительность.
Решите уравнения с помощью числовых методов с начала. Этот метод быстрее, но для неполиномиальных уравнений числовой решатель возвращает только первое решение, которое это находит. Можно использовать опцию AllRealRoots, чтобы заставить решатель искать другие действительные корни. Даже с этой опцией, набор решения может быть неполным. Используя AllRealRoots может значительно уменьшить производительность.
Когда вы решаете уравнение символически, решатель не всегда возвращает результаты в явной форме. Например, решатель может представлять решения с помощью RootOf:
solve(x^3 + x + 1, x)
![]()
Если у вас есть символьное решение, которое вы хотите аппроксимировать численно, использовать команду float:
S := float(%)
![]()
Присвойте отдельные решения переменных путем индексации в S:
xSol := S[3]
![]()
Используйте float, чтобы аппроксимировать решения символьной системы:
float(solve([x^3 + x^2 + 2*x = y, y^2 = x^2], [x, y]))

Аппроксимируя символьные решения численно, вы получаете полный набор решений. Например, решите следующее уравнение символически:
S := solve(sin(x^2) = 1/2, x)

Предположим, вы хотите получить числовые результаты вместо выражений, содержащих PI. Команда float возвращает бесконечный набор решения:
float(S)
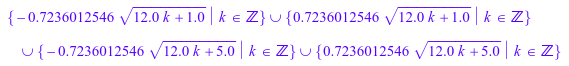
Чтобы постараться не получать символьные решения и возобновлять числовые методы, используйте команду numeric::solve. Если уравнение не является полиномом, числовой решатель возвращает только одно решение:
numeric::solve(sin(x^2) = 1/2, x)
![]()
Для полиномиальных уравнений числовой решатель возвращает все решения:
numeric::solve(4*x^4 + 3*x^3 + 2*x^2 + x + 5 = 0, x)
![]()
Когда названо опцией AllRealRoots, решатель не использует все комплексные корни. Например, когда вы символически решаете полиномиальное уравнение и аппроксимируете решения, вы получаете все решения:
numeric::solve(4*x^4 + 3*x^3 + 2*x^2 + x -1 = 0, x)
![]()
Чтобы ограничить набор решения действительными решениями только, используйте опцию AllRealRoots:
numeric::solve(4*x^4 + 3*x^3 + 2*x^2 + x - 1 = 0, x,
AllRealRoots)![]()
Используя numeric::solve, также можно решить систему полиномиальных уравнений:
numeric::solve([x^3 + 2*x = y, y^2 = x], [x, y])

Чтобы решить линейные системы численно, используйте команду numeric::linsolve. Например, решите следующую систему символически и численно:
linsolve([x = y - 1, x + y = 5/2], [x, y]); numeric::linsolve([x = y - 1, x + y = 5/2], [x, y])
![]()
![]()
Для неполиномиальных уравнений нет никакого общего метода нахождения всех решений численно. Когда вы решаете неполиномиальное уравнение или систему численно, и решения существуют, решатель возвращает только одно решение:
numeric::solve(sin(1/x) = x, x)
![]()
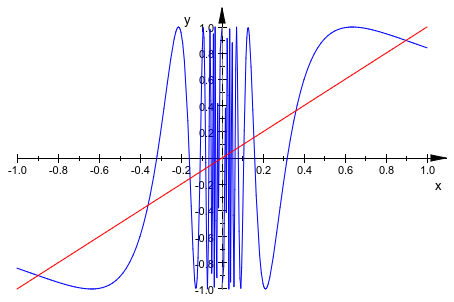
Это уравнение, очевидно, имеет больше чем одно решение:
plot(sin(1/x), x, x = -1..1)
Чтобы получить более действительные решения одного уравнения, содержащего одну переменную, вызовите числовой решатель с опцией AllRealRoots. Опция AllRealRoots не гарантирует, что решатель находит все существующие действительные корни. Например, опция помогает найти дополнительные решения для уравнения:
numeric::solve(sin(1/x) = x, x, AllRealRoots)
Warning: Problem in isolating search intervals. Some roots might be lost. [numeric::allRealRoots]

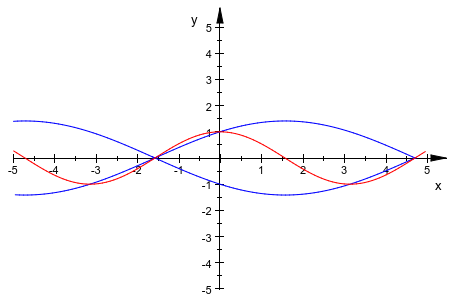
Для системы неполиномиального уравнения решатель также возвращает только одно решение. Строя уравнения, вы видите, что система имеет больше чем одно решение:
numeric::solve([sin(x) = y^2 - 1, cos(x) = y], [x, y]); plot(sin(x) = y^2 - 1, cos(x) = y)
![]()
Опция AllRealRoots не работает на системы:
numeric::solve([sin(x) = y^2 - 1, cos(x) = y], [x, y],
AllRealRoots)Error: Only one equation supported with 'AllRealRoots'. [numeric::solve]
Чтобы найти числовые приближения других решений, задайте интервалы, которые содержат решения. Можно использовать команду numeric::solve, который внутренне вызывает numeric::fsolve. Однако, чтобы ускорить ваши вычисления, вызовите numeric::fsolve непосредственно. Обратите внимание на то, что numeric::solve возвращает набор решений, и numeric::fsolve возвращает список:
numeric::solve([sin(x) = y^2 - 1, cos(x) = y],
[x = 2.5..3.5, y = -1.5..-0.5]);
numeric::fsolve([sin(x) = y^2 - 1, cos(x) = y],
[x = 4..5, y = -0.2..0.2])![]()
![]()
Опция MultiSolutions также служит, чтобы найти больше чем одно числовое приближение. Без этой опции числовой решатель ищет решение в заданном интервале и игнорирует любые решения, которые это находит за пределами интервала. Когда решатель находит первое решение в интервале, это останавливается и не ищет другие решения. Если вы используете MultiSolutions, решатель возвращает решения, найденные за пределами заданного интервала.
Если вы используете опцию MultiSolutions и не задаете интервала, числовой решатель возвращает только первое решение, которое это находит.
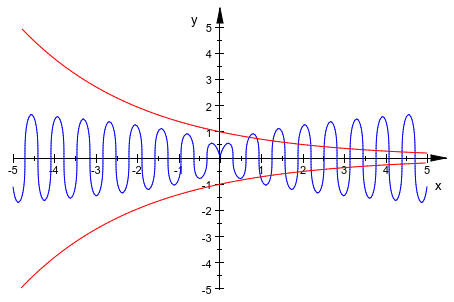
С опцией MultiSolutions также останавливается решатель после того, как это найдет первое решение в заданном интервале. Например, найдите несколько числовых приближений для следующей системы:
eqs := [x*sin(10*x) = y^3, y^2 = exp(-2*x/3)]: plot(x*sin(10*x) = y^3, y^2 = exp(-2*x/3))
Задайте интервал, где вы хотите искать решения. Например, считайте интервал x = 0..1, который содержит два решения:
plot(x*sin(10*x) = y^3, y^2 = exp(-2*x/3), x = 0..1, y = 0..1)
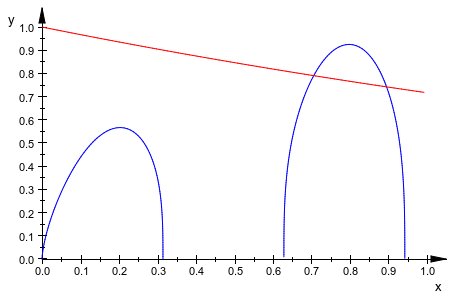
Вызовите numeric::solve или команду numeric::fsolve с опцией MultiSolutions. Оба решателя возвращают одно решение, которое принадлежит заданному интервалу и одному решению за пределами интервала:
numeric::fsolve(eqs, [x = 0..1, y = 0..1], MultiSolutions); numeric::solve(eqs, [x = 0..1, y = 0..1], MultiSolutions)
![]()
![]()
Определение интервала, который не содержит решений, может помочь вам найти больше приближений. В этом случае решатель не может найти решение в интервале и продолжает искать. Перед выходами решателя это может найти много решений вне заданного интервала:
numeric::fsolve(eqs, [x = -10..0, y = 0..1], MultiSolutions)

Если вы знаете интервал, содержащий решения полиномиального уравнения, можно значительно ускорить числовые приближения. Чтобы найти одно решение в заданном интервале, используйте команду numeric::realroot. Команда возвращает действительные решения и не использует комплексные единицы:
numeric::realroot(1/4*x^4 + x^3 + x + 1 = 0, x = -5..0)
![]()
Также можно задать интервал и искать все подынтервалы, которые могут содержать действительные корни. Команда numeric::realroots возвращает полный список таких подынтервалов:
numeric::realroots(1/4*x^4 + x^3 + x + 1 = 0, x = -5..0)
![]()
Если уравнение, которое вы решаете, является полиномом, каждый подынтервал содержит точно один корень. Для неполиномиальных уравнений numeric::realroots может возвратить подынтервалы, которые не содержат корней. numeric::realroots гарантирует, что поисковый интервал не содержит действительных корней вне возвращенных подынтервалов.
Нет никакого общего способа решить произвольную секунду - или обыкновенное дифференциальное уравнение (ODE) высшего порядка. Часто, такое уравнение не имеет символьного решения. В некоторых случаях решение существует, но оно может быть представлено только специальными функциями. Например, решение следующего ОДУ второго порядка включает функцию ошибок erf:
o:=ode({y''(t) = t*y'(t), y(0) = 0, y'(0) = 1/3}, y(t)):
ode::solve(o)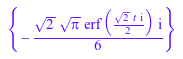
Предположим, вам не нужно точное символьное решение, но вы хотите аппроксимировать решение для нескольких значений параметра t. Для числовых приближений решений ОДУ MuPAD обеспечивает две функции:
numeric::odesolve возвращает числовое приближение решения в конкретной точке.
numeric::odesolve2 возвращает функцию, представляющую числовое приближение решения.
Обе функции принимают или ОДУ первого порядка или систему ОДУ первого порядка. Чтобы решить уравнение высшего порядка, преобразуйте его в систему уравнений первого порядка. Например, представляйте ОДУ второго порядка, который вы решили символически как система двух уравнений первого порядка![]() :. вектором решения для этой системы является
:. вектором решения для этой системы является Y = [y, z].
Функциональный numeric::odesolve требует, чтобы система ОДУ первого порядка (динамическая система) была представлена процедурой:
f := proc(t, Y) begin [Y[2], t*Y[2]] end_proc
![]()
Второй параметр numeric::odesolve является областью значений, в которой вы хотите решить ОДУ. Третий параметр является списком начальных условий (![]() ). Аппроксимируйте решения y (t) для t = 1, t = 3, и
). Аппроксимируйте решения y (t) для t = 1, t = 3, и![]() :
:
numeric::odesolve(f, 0..1, [0, 1/3]); numeric::odesolve(f, 0..3, [0, 1/3]); numeric::odesolve(f, 0..1/127, [0, 1/3])
![]()
![]()
![]()
MuPAD также предлагает альтернативный способ сгенерировать параметры для ОДУ числовые решатели:
Задайте свою задачу с начальными значениями как список или набор:
IVP := {y''(t) = t*y'(t), y(0) = 0, y'(0) = 1/3}:Задайте набор полей, по которым вы хотите получить решение:
fields := [y(t), y'(t)]:
Преобразуйте задачу с начальными значениями и поля в процедуру, приемлемую numeric::odesolve. Функциональный numeric::ode2vectorfield генерирует необходимую процедуру:
[ODE, t0, Y0] := [numeric::ode2vectorfield(IVP, fields)]
![]()
Теперь вызовите numeric::odesolve, чтобы аппроксимировать решение в особых значениях t:
numeric::odesolve(ODE, t0..1, Y0)
![]()
Функциональный numeric::odesolve2 также требует, чтобы система ОДУ первого порядка (динамическая система) была представлена процедурой. Чтобы сгенерировать параметры для numeric::odesolve2, используйте следующие шаги:
Задайте свою задачу с начальными значениями как список или набор:
IVP := {y''(t) = t*y'(t), y(0) = 0, y'(0) = 1/3}:Задайте набор полей, по которым вы хотите получить решение:
fields := [y(t), y'(t)]:
Преобразуйте задачу с начальными значениями и поля в процедуру, приемлемую numeric::odesolve2. Функциональный numeric::ode2vectorfield генерирует необходимую процедуру:
ODE := numeric::ode2vectorfield(IVP, fields)
![]()
Теперь вызовите numeric::odesolve2, чтобы аппроксимировать решение:
numApprox := numeric::odesolve2(ODE)
![]()
Используя функцию, сгенерированную numeric::odesolve2, найдите числовое приближение в любой точке. Например, найдите числовые решения для значений t = 1, t = 3, и![]() . Вы получаете те же результаты как с
. Вы получаете те же результаты как с numeric::odesolve, но синтаксис короче:
numApprox(1); numApprox(3); numApprox(1/127)
![]()
![]()
![]()
Постройте числовое решение с помощью функции, сгенерированной numeric::odesolve2. Функциональный numApprox возвращает список [y(t), y'(t)]. При графическом выводе решения y(t) используйте скобки, чтобы извлечь первую запись списка решений:
plotfunc2d(numApprox(t)[1], t = 0..3)
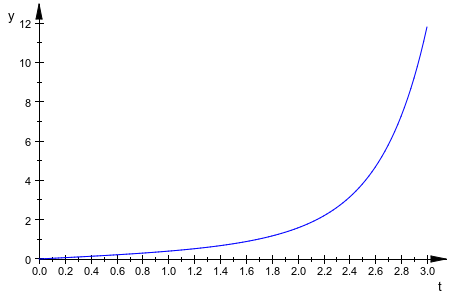
Используйте numeric::odesolve2, чтобы найти числовые приближения для следующей системы ОДУ:
IVP := {x'(t) = -y(t) + x(t)^2,
y'(t) = 10*x(t) - y(t)^2,
x(0) = 1, y(0) = 1}:
fields := [x(t), y(t)]:
ODE := numeric::ode2vectorfield(IVP, fields):
numApprox := numeric::odesolve2(ODE)![]()
Постройте числовые решения для x(t) и y(t) в одном графике:
plotfunc2d(numApprox(t)[1], numApprox(t)[2], t = 0..20)
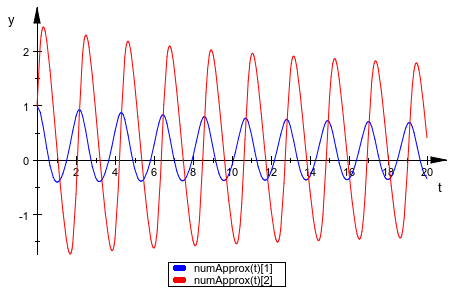
Используйте функцию построения графика plot::Curve2d, чтобы сгенерировать параметрический график числового решения:
curve := plot::Curve2d([numApprox(t)[1], numApprox(t)[2]],
t = 0..20):
plot(curve)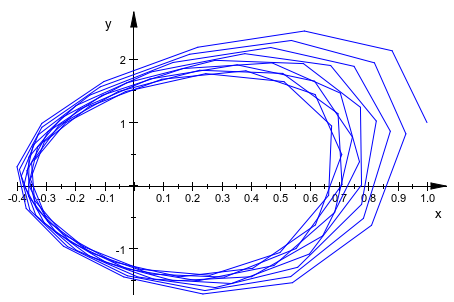
Также используйте plot::Ode2d или plot::Ode3d.