ode:: exponentsЭкспоненты линейного обыкновенного дифференциального уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
ode::exponents(Ly, y(x), p)
ode::exponents возвращает набор экспонент гомогенного линейного дифференциального уравнения в данной точке.
ode::exponents(Ly, y(x), p) возвращает набор (локальных) экспонент Ly в месте p. Если место является бесконечностью затем, каждый использует
вместо этого. Они заданы как корни (в алгебраическом замыкании ℚ (x)) определяющего уравнения (c.f. ode::indicialEquation) Ly, таким образом, набор экспонент может быть пустым, видеть Пример 2.
Мы вычисляем экспоненты следующего дифференциального уравнения в регулярной точке 0 и в особых точках -1 и infinity:
Ly := diff(y(x),x$2)+4/(x+1)*diff(y(x),x)+2/(x+1)^2*y(x)
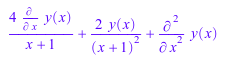
ode::exponents(Ly, y(x), x)
ode::exponents(Ly, y(x), x+1)
ode::exponents(Ly, y(x), 1/x)
Это может произойти, что в месте набор экспонент пуст; это соответствует неправильной особой точке:
Ly := (2*x+4)*diff(y(x),x)/(2*x+x^2-2)-2*y(x)/(2*x+x^2-2)-
(4*x+x^2)/(2*x+x^2-2)*diff(y(x),x$2)+diff(y(x),x$3)
ode::exponents(Ly, y(x), 1/x)
ode::exponents(Ly, y(x), x^2+2*x-2)
|
Гомогенное линейное дифференциальное уравнение по ℚ (x). |
|
Зависимая функция |
|
Неприводимый полином в |
set, возможно пустой.