polylib:: splitfieldПоле Splitting полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
polylib::splitfield(p)
Учитывая полиномиальный p по полю K в одном неопределенном X, polylib::splitfield(p) возвращает простое полевое расширение F K и некоторых элементов α 1, …, α n F, такого, который
партнер p, и таким образом, что F является самым маленьким расширением K, содержащего весь i α.
Если вход является многочленным выражением, как в Примере 1, это обработано как полином по rationals.
Полиномиальный p не должен быть неприводимым.
Имя для примитивного элемента полевого расширения сгенерировано с помощью genident и поэтому отличается в каждом вызове polylib::splitfield, даже если тот же полином передается.
MuPAD® должен смочь учесть полиномы по содействующему полю p.
Содействующее поле должно быть совершенным. В противном случае это может произойти, который не отключает polylib::splitfield.
Мы примыкаем
к rationals:
polylib::splitfield(x^2+1)
Вызов polylib::splitfield становится более интересным для полиномов для степени по крайней мере 3:
polylib::splitfield(x^3-2)
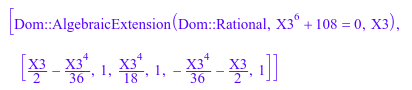
В этом примере мы перерабатываем поле одномерных рациональных функций (поле частных одномерных полиномов) по rationals:
R:=Dom::DistributedPolynomial([x], Dom::Rational): F:=Dom::Fraction(R): f:=poly(y^3-x,[y],F): polylib::splitfield(f)
|
Одномерный полином по полю или одномерное многочленное выражение |
polylib::splitfield возвращает список двух операндов: первый является разделяющим полем полинома, т.е. Dom::AlgebraicExtension содействующего звонка; второй является списком всех корней полинома в разделяющем поле, каждый корень, сопровождаемый его кратностью.