Dom:: AlgebraicExtensionПростые алгебраические полевые расширения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Dom::AlgebraicExtension(F,f)
Dom::AlgebraicExtension(F,f,x)
Dom::AlgebraicExtension(F,f1 = f2)
Dom::AlgebraicExtension(F,f1 = f2,x)
Dom::AlgebraicExtension(F,f)(g)Dom::AlgebraicExtension(F, f)(rat)Для данного поля F и полиномиального f ∈ F[x], Dom::AlgebraicExtension(F, f, x) создает поле F[x]/<f> класса вычетов.
Dom::AlgebraicExtension(F, f1=f2, x) делает то же самое для f = f 1 - f 2.
Dom::AlgebraicExtension(F, f, x) создает поле F[x]/<f> классов вычетов полиномов f по модулю. Это поле может также быть записано как F[x]/<f>, поле классов вычетов рациональных функций f по модулю.
x параметра может быть не использован, если f является одномерным полиномом или многочленным выражением, которое содержит точно одно неопределенное; это затем взято, чтобы быть неопределенным появлением в f.
Поле F должно иметь нормальное представление.
f не должен быть постоянным полиномом.
f должен быть неприводимым; это не проверяется.
f может быть полиномом по содействующему звонку, отличающемуся от F или многомерному; однако, должно быть возможно преобразовать его в одномерный полином по F. Смотрите Пример 2.
Dom::AlgebraicExtension(F, f)(g) создает класс вычетов g f по модулю.
Если rat имеет числитель и знаменатель p и q, соответственно, то Dom::AlgebraicExtension(F,f)(rat) равняется Dom::AlgebraicExtension(F,f)(p), разделенному на Dom::AlgebraicExtension(F,f)(q).
Если F имеет Ax::canonicalRep, то Ax::canonicalRep.
Cat::Field, Cat::Algebra (F), Cat::VectorSpace (F)
Если F является Cat::DifferentialRing, то Cat::DifferentialRing.
Если F является Cat::PartialDifferentialRing, то Cat::PartialDifferentialRing.
Мы примыкаем к кубическому корневому alpha 2 к rationals.
G := Dom::AlgebraicExtension(Dom::Rational, alpha^3 = 2)
Третья степень кубического корня 2 равняется 2, конечно.
G(alpha)^3
Трассировка α является нулем:
G::conjTrace(G(alpha))
Можно также создать случайные элементы:
G::random()
Наземное поле может быть самим алгебраическим расширением. Таким образом возможно создать башню полей. В следующем примере алгебраическое расширение задано с помощью примитивного элемента alpha и примитивного элемента, beta дальнейшего расширения задан с точки зрения alpha. В таких случаях, когда минимальное уравнение содержит больше чем один идентификатор, третий аргумент к Dom::AlgebraicExtension должен быть явно задан.
F := Dom::AlgebraicExtension(Dom::Rational, alpha^2 = 2): G := Dom::AlgebraicExtension(F, bet^2 + bet = alpha, bet)
Мы хотим задать расширение поля частей звонка двумерных полиномов по rationals.
P:= Dom::DistributedPolynomial([x, y], Dom::Rational): F:= Dom::Fraction(P): K:= Dom::AlgebraicExtension(F, alpha^2 = x, alpha)
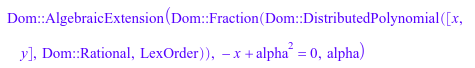
Теперь. Конечно, функция квадратного корня имеет обычную производную; обратите внимание, что это
может быть выражено как
:
diff(K(alpha), x)
С другой стороны, производная
относительно y является нулем, конечно:
diff(K(alpha), y)
Мы не должны использовать D здесь. Это работает, только если мы запускаем нашу конструкцию со звонка одномерных полиномов:
P:= Dom::DistributedPolynomial([x], Dom::Rational): F:= Dom::Fraction(P): K:= Dom::AlgebraicExtension(F, alpha^2 = x, alpha): D(K(alpha))
|
Наземное поле: область категории |
|
Полиномы или многочленные выражения |
|
Идентификатор |
|
Элемент класса вычетов, который будет задан: полином по |
|
Рациональная функция, которая принадлежит классу вычетов, который будет задан: выражение, числитель которого и знаменатель могут быть преобразованы в полиномы по |
| "нуль" | нулевой элемент полевого расширения |
| "один" | единичный элемент полевого расширения |
| "groundField" | наземное поле расширения |
| "minpoly" | минимальный полиномиальный |
| "градус" | степень расширения, т.е. |
| "переменная" | неизвестный из минимального полиномиального |
| "характеристика" | характеристика, которая всегда равняется характеристике наземного поля. Эта запись только существует, если характеристика наземного поля известна. |
| "degreeOverPrimeField" | размерность поля, когда просматривается как векторное пространство по лучшему полю. Эта запись только существует, если наземное поле является лучшим полем, или его степень по его лучшему полю известна. |