productОпределенные и неопределенные продукты
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
product(f,i) product(f,i = a .. b) product(f,i = RootOf(p, <x>)) product(f,i in RootOf(p, <x>)) product(f,i in {x1, x2, …})
product(f, i) вычисляет неопределенный продукт f (i) относительно i, т.е. закрытая форма g, таким образом что![]() .
.
product(f, i = a..b) пытается найти закрытое представление формы продукта![]() .
.
product (f, i = RootOf(p, x)) вычисляет продукт f (i) по корням полиномиального p.
product(f, i in { x1, x2, …}) вычисляет продукт![]() .
.
product служит для упрощения символьных продуктов. Это не должно использоваться для умножения конечного числа условий: если a и b являются целыми числами типа DOM_INT, вызов, _mult(f $ i = a..b) более эффективен, чем product(f, i = a..b).
product(f, i) вычисляет неопределенный продукт f относительно i. Это - выражение g, таким образом что![]() .
.
Это неявно принято, что i пробегает целые числа только.
product(f, i = a..b) вычисляет определенный продукт с i, запускающимся от a до b. Это неявно принято тот a ≤ b; это - ошибка, если это противоречиво.
a и b не должны быть числами кроме целых чисел.
Если b-a является целым числом, явный продукт, f (a) f (a + 1) … f (b) возвращен, если это имеет не больше, чем 1 000 факторов.
product (f, i = RootOf(p, x)) вычисляет определенный продукт с i, пробегающим корни полиномиального p в x согласно их кратности, т.е. ряд факторов равен степени p.
Вызовы product (f, i = RootOf(p, x)) и product (f, i in RootOf(p, x)) эквивалентны.
Система отвечает на символьный звонок product, если она не может вычислить закрытое представление формы продукта.
Каждый из следующих двух вызовов вычисляет продукт 1 2 3 4 5:
product(i, i = 1..5) = _mult(i $ i = 1..5)
![]()
Однако использование _mult обычно более эффективно, когда контуры являются целыми числами типа DOM_INT.
Существует закрытая форма этого определенного продукта от 1 до n:
product(i, i = 1..n)
![]()
Поскольку верхний контур является символьным идентификатором, _mult не может обработать этот продукт:
_mult(i $ i = 1..n)
![]()
Соответствующий неопределенный продукт:
product(i, i)

Неопределенное и определенный продукт 2 i + 1:
product(2*i + 1, i)
![]()
product(2*i + 1, i = 1..n)
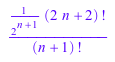
Контуры могут быть символьными выражениями или![]() также:
также:
product(i^2/(i^2 - 1), i = 2..infinity)
![]()
Система не может найти закрытые формы следующих двух продуктов и отвечает на символьные звонки product:
delete f: product(f(i), i)
![]()
product((1 + 2^(-i)), i = 1..infinity)
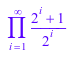
Приближение может быть вычислено численно через float:
float(%)
![]()
Также можно вызвать numeric::product непосредственно. Это обычно более эффективно, поскольку это пропускает символьные вычисления, выполняемые product:
numeric::product((1 + 2^(-i)), i = 1..infinity)
![]()
Некоторые продукты по корням полинома:
product(1 + 1/x, x = RootOf(x^2 - 5*x + 6))
![]()
product(r+c, r = RootOf(x^3 + a*x^2 + b*x + c, x))
![]()
Кратность корней учтена:
product(x+2, x in RootOf(x^5))
![]()
MuPAD® находит закрытые формы для продуктов рациональных выражений. В других случаях отвечают на символьный звонок product:
product(sin(r), r = RootOf(x^2 - PI^2/4, x))
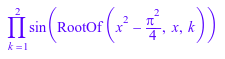
Приближение может быть вычислено численно через float:
float(%)
![]()
Некоторые продукты по элементам набора:
product(x+2, x in {2,4,8})![]()
product(a*x, x in {3, b, 5})![]()
Одинаковые объекты появляются только однажды в наборе. Поэтому второй a в следующем примере не имеет никакого эффекта на результат:
product(-x, x in {a,a,7,b})![]()
|
Арифметическое выражение в зависимости от |
|
Список продукции: идентификатор или индексированный indentifier |
|
Контуры: арифметические выражения |
| |
|
Неопределенный |
Продукт по корням полинома вычисляется через polylib::resultant.