sumОпределенное и неопределенное суммирование
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Для функции sum в MATLAB® смотрите sum.
sum(f,i) sum(f,i = a .. b) sum(f,i = RootOf(p, x))
sum(f, i) вычисляет символьное антиразличие f (i) относительно i.
sum(f, i = a..b) пытается найти закрытое представление формы суммы![]() .
.
sum служит для упрощения символьных сумм (дискретный аналог интегрирования). Это не должно использоваться для того, чтобы просто добавить конечное число условий: если a и b являются целыми числами типа DOM_INT, вызов, который _plus(f $ i = a..b) дает желаемому результату, в то время как sum(f, i = a..b) может возвратиться неоцененный. expand может использоваться, чтобы суммировать такую неоцененную конечную сумму. Смотрите Пример 3.
sum(f, i) вычисляет неопределенную сумму f относительно i. Это - выражение g, таким образом что f (i) = g (i + 1) - g (i).
Это неявно принято, что i пробегает целые числа только.
sum(f, i = a..b) вычисляет определенную сумму с i, запускающимся от a до b.
Если a и b являются числами, то они должны быть целыми числами.
Если b - a является неотрицательным целым числом, то явная сумма f (a) + f (a + 1) + … + f (b) возвращен, при условии, что эта сумма имеет не больше, чем 1 000 условий.
sum(f, i = RootOf(p, x)) вычисляет сумму с расширением i по всем корням полиномиального p относительно x.
Если f будет рациональной функцией i, закрытая форма суммы будет найдена.
Смотрите пример 2.
Система отвечает на символьный звонок sum, если это не может вычислить закрытое представление формы суммы.
Бог символьные суммы без символьных параметров может быть оценен численно через float или numeric::sum. Cf. Пример 4.
Мы вычисляем некоторые неопределенные суммы:
sum(1/(i^2 - 1), i)
![]()
sum(1/i/(i + 2)^2, i)
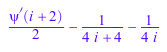
sum(binomial(n + i, i), i)

Мы вычисляем некоторые определенные суммы. Обратите внимание на то, что![]() допустимые контуры:
допустимые контуры:
sum(1/(i^2 + 21*i), i = 1..infinity)
![]()
sum(1/i, i = a .. a + 3)
![]()
expand(%)
![]()
Мы вычисляем некоторые суммы по всем корням полинома:
sum(i^2, i = RootOf(x^3 + a*x^2 + b*x + c, x))
![]()
sum(1/(z + i), i = RootOf(x^4 - y*x + 1, x))
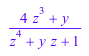
sum может вычислить конечные суммы, если неопределенное суммирование успешно выполняется:
sum(1/(i^2 + i), i = 1..100)
![]()
_plus приводит к тому же результату более быстро, если количество слагаемых является маленьким:
_plus(1/(i^2 + i) $ i = 1..100)
![]()
В таких случаях sum намного более эффективен, чем _plus, если количество слагаемых является большим:
sum(1/(i^2 + i), i = 1..10^30)
![]()
Конечные суммы, для которых никакое неопределенное суммирование не возможно, расширены, если у них есть не больше, чем 1 000 условий:
sum(binomial(n, i), i = 0..4)
![]()
Приложение expand необходимо, чтобы расширить биномы:
expand(%)
![]()
Конечные суммы больше чем с 1 000 условий не расширены:
sum(binomial(n, i), i = 0..1000)
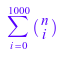
Вы можете использовать expand здесь, чтобы расширить сумму и получить огромное выражение. Если вы действительно хотите сделать это, мы рекомендуем использовать _plus непосредственно.
Однако, если один из контуров является символьным, то _plus не может использоваться:
_plus(1/(i^2 + i) $ i = 1..n)
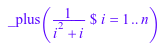
_plus(binomial(n, i) $ i = 0..n)
![]()
sum(1/(i^2 + i), i = 1..n), sum(binomial(n, i), i = 0..n)
![]()
Следующая бесконечная сумма не может быть вычислена символически:
sum(ln(i)/i^5, i = 1..infinity)

Мы получаем приближение с плавающей точкой через float:
float(%)
![]()
Также функциональный numeric::sum может использоваться непосредственно. Это обычно намного быстрее, чем применение float, поскольку это избегает издержек sum, пытающегося вычислить символьное представление:
numeric::sum(ln(i)/i^5, i = 1..infinity)
![]()
|
Арифметическое выражение в зависимости от |
|
Индекс суммирования: идентификатор или индексированный идентификатор |
|
Контуры: арифметические выражения |
|
Полином типа |
|
Неопределенный из |
Функциональный sum реализует алгоритм Абрамова для рациональных выражений, алгоритм Госпера для гипергеометрических выражений и алгоритм Цайльбергера для определенного суммирования голономных выражений.